Курсовая работа: Сигналы и процессы в радиотехнике (СиПРТ)

Министерство образования и науки Украины

Севастопольский национальный технический университет

КУРСОВАЯ РАБОТА

по дисциплине

«Сигналы и процессы в радиотехнике»

Выполнил студент: Гармаш М. А.

Группа: Р-33 д

Номер зачётной книжки: 212467

Допущен к защите

Защищен с оценкой

Руководитель работы

__________________

Агафонцева О. И.

__________________ « »__________ 2003 г. « »________ 2003 г.

Севастополь

2003

Содержание

1 ЗАДАНИЕ

2 ЗАДАНИЕ

3 ЗАДАНИЕ

4 ЗАДАНИЕ

5 ЗАДАНИЕ

6 ЗАДАНИЕ

7 ЗАДАНИЕ

ПЕРЕЧЕНЬ ССЫЛОК

Задание 1

Условие:

На безынерционный нелинейный элемент, ВАХ которого аппроксимирована кусочно - ломаной линией с крутизной линейного участка и напряжением отсечки подано напряжение .

Требуется:

1. Составить уравнение ВАХ нелинейного элемента.

2. Рассчитать и построить спектр выходного тока вплоть до десятой гармоники. Построить временные диаграммы входного напряжения, тока, протекающего через элемент и его первых четырёх гармоник.

3. Определить углы отсечки и напряжения смещения , при которых в спектре тока отсутствует: а) вторая гармоника; б) третья гармоника.

4. Найти угол отсечки и напряжение смещения , соответствующие максимуму амплитуды третьей гармоники для случая, когда .

5. Построить колебательную характеристику и описать её особенности. Найти напряжение смещения , соответствующее ее линейности.

Исходные данные приведены ниже:

S=45ма/А; U1=-3 В; U0=-2 В; Um =2 В.

Решение:

1. Воспользовавшись [1] составим уравнение ВАХ нелинейного элемента , которое определяется по формуле

(1.1)

Импульсы выходного тока можно рассчитать по формуле:

(1.2)

График изображен на рисунке 1.1

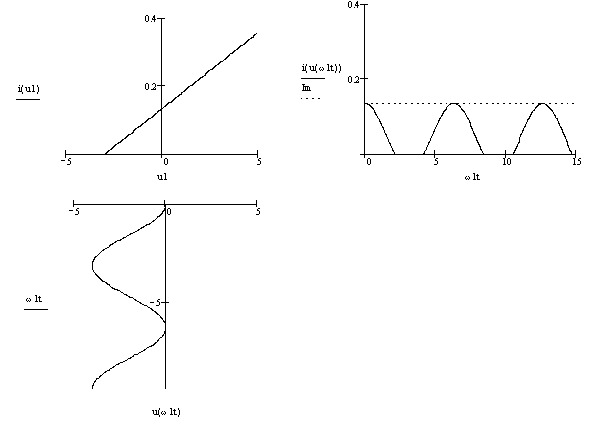
Рисунок 1.1 -

а) График ВАХ уравнения нелинейного элемента.

б) График выходного тока .

в) График входного напряжения.

2. Рассчитаем спектр выходного тока. Известно, что спектр тока рассчитывается по формуле:

, (1.3)

где - амплитуда -ой гармоники тока;

- амплитуда импульсов тока; n- номер гармоники (n=0,1,…,10);

- коэффициенты Берга,

Q-угол отсечки, определяемый по формуле:

. (1.3)

Подставив численные значения находим Q=2.094. Строим спектрограмму выходного тока используя [3]. Спектр показан на рисунке 1.2

(1.4) (1.6)

(1.5)

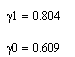
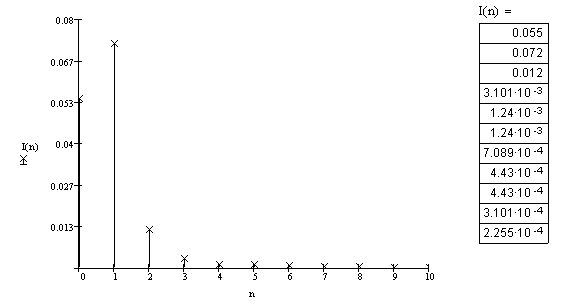Рисунок 1.2 – Спектрограмма выходного тока

Теперь построим графики первых четырёх гармоник при помощи [3]:

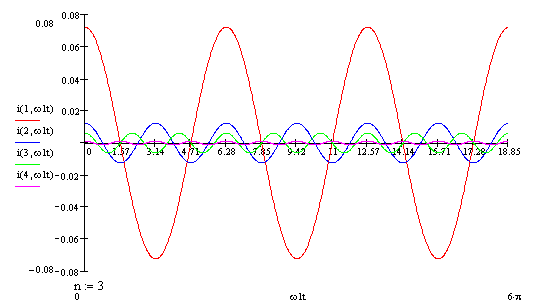
Рисунок 1.3 - графики первых четырёх гармоник

3. Определим угол отсечки и смещение, при котором в спектре тока отсутствует n-я гармоника, что в соответствии с (1.3), можно определить путём решения уравнения :

. (1.7)

Результат показан ниже :

для 2 гармоники Q1 = 0, Q2 = 180;

для 3 гармоники Q = 0, Q2 = 90, Q = 180;

Проведём суммирование гармоник:

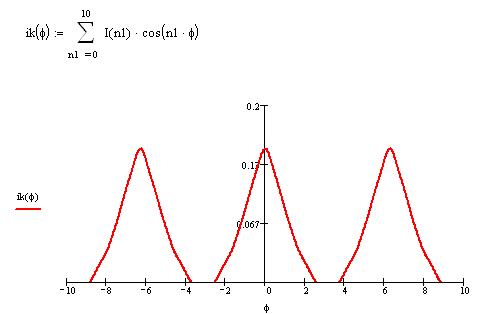
Рисунок 1.4 - сумма первых десяти гармоник

4. Угол отсечки, соответствующий максимуму n-ой гармоники в спектре тока (при ) определяется по формуле:

(1.8)

Угол отсечки равен 60. Определим соответствующее напряжение смещения U0 из формулы(1.3).В итоге получим :

Подставляя численные значения получим U0= - 2В.

5. Колебательная характеристика нелинейного элемента определяется зависимостью амплитуды первой гармоники тока , протекающего через нелинейный элемент, от амплитуды входного напряжения:

Поскольку >U1, то вид характеристики определяется по формуле:

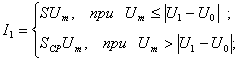. (1.9)

где- средняя крутизна, определяемая cоотношением:

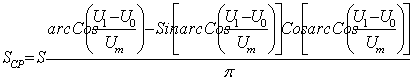: . (1.10)

(1.11))

Построим колебательную характеристику используя формулу (1.6) с учетом этой

Колебательная характеристика изображена на рисунке 1.5:

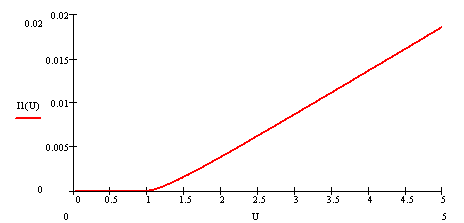
Рисунок 1.5 – Колебательная характеристика

Задание 2

Условие:

На вход резонансного умножителя частоты, выполненного на полевом транзисторе (рисунок 2) подано напряжение , где - частота сигнала. Нагрузкой умножителя является колебательный контур с резонансной частотой , ёмкостью и добротностью . Коэффициент включения катушки -. Сток - затворная характеристика транзистора задана в виде таблицы 3 и может быть аппроксимирована в окрестности полиномом:

Таблица 1 - Характеристика транзистора к заданию 2

, В	-12	-11	-10	-9	-8	-7	-6	-5	-4	-3	-2	-1	0
, мА	1,6	1,8	2,1	2,5	3	3,8	4,8	6	7,5	9	12	15	20

Требуется:

1. Построить ВАХ полевого транзистора. Изобразить временные диаграммы входного напряжения, тока стока и выходного напряжения умножителя.

2. Определить коэффициенты аппроксимирующего полинома .

3. Рассчитать спектр тока стока и спектр выходного напряжения умножителя. Построить соответствующие спектрограммы и найти коэффициент нелинейных искажений выходного напряжения.

4. Рассчитать нормированную АЧХ контура, построить её в том же частотном масштабе, что и спектрограммы, расположив их друг под другом.

5. Рассчитать индуктивность и полосу пропускания контура.

Исходные данные :

U0= -3,5 B, Um=3 B, f1=2 МГц C=120 пФ, P=0,2

Примечание: при расчётах

положить равным 12 В.

Рисунок 2.1 - Схема удвоителя частоты.

Решение:

1. По значениям, приведенным в таблице 3, построим ВАХ полевого транзистора. Изобразим временные диаграммы входного напряжения:

U(t)=U0+Um*cos(wt) (2.1)

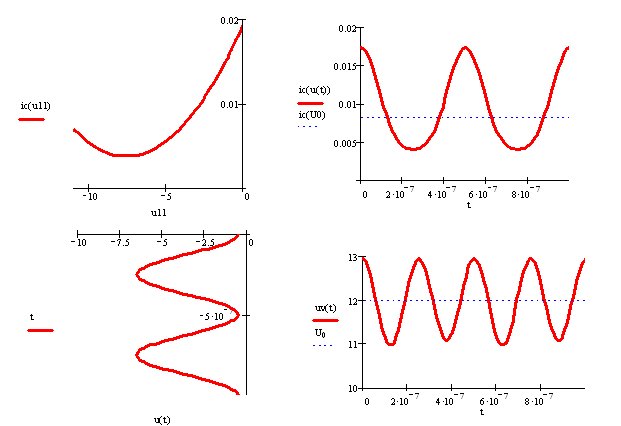
Рисунок 2.2 -

а) сток-затворная характеристика транзистора.

б) ток стока.

в) входное напряжение транзистора.

2. Коэффициенты определим, используя метод узловых точек. Выберем три точки (Напряжения соответственно равные ), в которых аппроксимирующий полином совпадает с заданной характеристикой:

u 1 = - 3,5В u 2= -0,5В u3=--7,5В

Затем, подставляя в полином значения тока, взятые из таблицы 3 и напряжения, соответствующие этим точкам, получают три уравнения.

(2.2)

Решая систему уравнений (2.2), используя [3], с помощью процедуры Given-Minerr , определим искомые коэффициенты полинома :

a0= 8,25 мА ; a1= 2,2 мА/В a2= 0,26 мА/В2

Проведем расчёт аппроксимирующей характеристики в рабочем диапазоне напряжений по формуле:

(2.3)

3. Спектр тока стока рассчитаем с использованием метода кратного аргумента [2] . Для этого входное напряжение подставим в аппроксимирующий полином и приведем результат к виду:

, (2.4)

где - постоянная составляющая; - амплитуды первой и второй гармоник соответственно;.После подстановки входного напряжения в полином, получим:

(2.5) (2.6)

(2.7)

Подставляя числовые значения коэффициентов a0, a1, a3 и амплитудное значение входного сигнала Um, получим :

I0= 9.45 I1=6.6 I2=1.2

Изобразим спектр тока стока на рисунке 2.4, используя [3]:

Рисунок 2.3 – Спектр тока стока

Рассчитаем cпектр выходного напряжения, которое создаётся током (2.4).Он будет содержать постоянную составляющую и две гармоники с амплитудами и начальными фазами и

, (2.8)

где - определим по формулам:

; (2.9)

; (2.10)

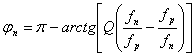, (2.11)

где - напряжение источника питания;

- сопротивление катушки индуктивности;

- характеристическое сопротивление контура; - резонансная частота; - номер гармоники ().

Подставив числовые значения для f1, Ec=12, I0, Q, C, r и рассчитав промежуточные значения:

r= 331,573 Ом , r = 5,526 Ом; R0 = 19890 Oм; Fр =4МГц;

рассчитаем спектр выходного напряжения с помощью [3]:

U0 =11,99 В, U1 = 0.058 В , U2= 0.955 В.

Изобразим спектр амплитуд и фаз выходного напряжения на рисунке 2.5:

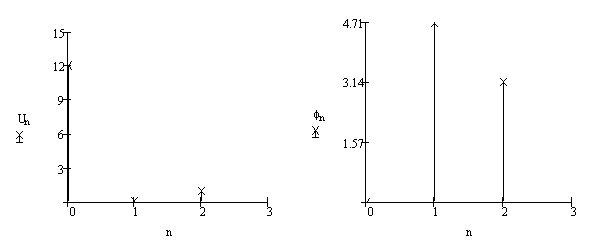Рисунок 2.4 – Спектр амплитуд и фаз выходного напряжения

Определим коэффициент нелинейных искажений выходного напряжения по следующей формуле:

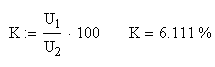
4. Найдем- нормированную амплитудно-частотную характеристику контура, которую рассчитаем по формуле:

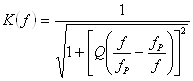(2.12)

Изобразим нормированную амплитудно-частотную и фазо-частотную характеристики контура на рисунке 2.6, используя [3]:

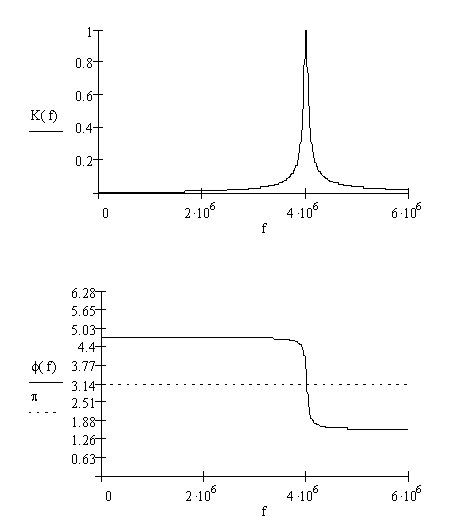
Рисунок 2.5 - Амплитудно-частотная и фазо-частотная характеристики контура

5. Используя формулу [1] для индуктивности контура:

L=r/2*p*fp, (2.13)

найдём индуктивность контура L= 520.8 мкГн.

Графическим способом на уровне 0.707 определяем полосу пропускания, которая равна Df= 1,3105 кГц.

Задание 3

Условие:

На вход амплитудного детектора вещательного приёмника, содержащего диод с внутренним сопротивлением в открытом состоянии и - фильтр, подаётся амплитудно-модулированный сигнал и узкополосный шум с равномерным энергетическим спектром в полосе частот, равной полосе пропускания тракта промежуточной частоты приёмника и дисперсией .

Требуется:

1. Привести схему детектора и определить ёмкость фильтра нижних частот.

2. Рассчитать дисперсию входного шума и амплитуду несущего колебания .

3. Определить отношение сигнал/помеха на входе и выходе детектора (по мощности) в отсутствии модуляции.

4. Рассчитать постоянную составляющую и амплитуду переменной составляющей выходного сигнала.

5. Построить на одном рисунке ВАХ диода, полагая напряжение отсечки равным нулю, а также временные диаграммы выходного напряжения, тока диода и напряжения на диоде.

Исходные данные приведены ниже:

R1=20 Ом ; R=10 кОм ; M=30% ; W0=4.6

Решение:

1. На рис.3.1 изобразим схему детектора:

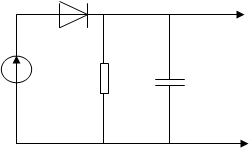
Рисунок 3.1 - Схема детектора.

Постоянную времени фильтра детектора выберем из условия

, (3.1)

где - частота несущего колебания;

- максимальная частота в спектре модулирующего сигнала.

Для того чтобы удовлетворить условию (3.1) следует выберем как среднее геометрическое

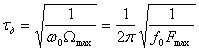. (3.2)

где кГц (промежуточная частота),

кГц.

Рассчитав по формуле (3.2),находим, что =4 мкс .Далее определим ёмкость фильтра по формуле:

. (3.3)

Расчет производим в [M] и находим ,что C= 0,4 нФ.

2. Дисперсию входного шума определяют по формуле

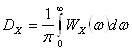, (3.4)

где - энергетический спектр шума.

Интегрировать будем ,по условию задачи, в полосе частот . ,

поскольку спектр шума равномерен, а за пределами этой полосы – равен нулю. Определим дисперсию входного шума по формуле (3.4) с помощью [3]:

Dx=0.125 В2.

Вычислим амплитуду несущего колебания в соответствии с задачей по формуле :

. (3.5)

Подставив исходные значения получим: =3.537 В.

3. Определяем отношение сигнал/помеха на входе (по мощности) детектора :

. (3.6)

Подставив исходные значения получим:: h=50

Определяем отношение сигнал/помеха на выходе детектора по формуле :

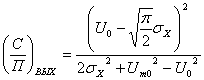, (3.7)

где - среднеквадратическое отклонение входного шума;

- постоянная составляющая выходного напряжения детектора при одновременном воздействии сигнала (несущей) и шума. Сначала находим СКО=0.354 В. Далее определяем постоянную составляющую формуле

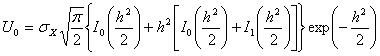, (3.8)

где -функции Бесселя нулевого и первого порядков (модифицированные) соответственно. Производим вычисления с помощью [3] находим =3,555 В. Подставляем полученные значения , СКО находим, что сигнал/помеха на выходе равен:

4. Напряжение на выходе детектора в отсутствии шума прямопропорционально амплитуде входного сигнала

, (3.9)

где - коэффициент преобразования детектора, который определяется по формуле:

. (3.10)

где Q-угол отсечки.

Угол отсечки тока определим решением трансцендентного уравнения:

. (3.11)

Решение уравнения (3.11) произведем в [3].Решив (3.11) находим Q=21.83, а К0=0.928.

Раскрыв скобки в выражении (3.9), приведём выражение для выходного сигнала к виду

, (3.12)

где: - постоянная составляющая выходного сигнала;

- амплитуда выходного сигнала.

Подставив значения, получим:

Построим сигнал на выходе детектора:

. (3.13)

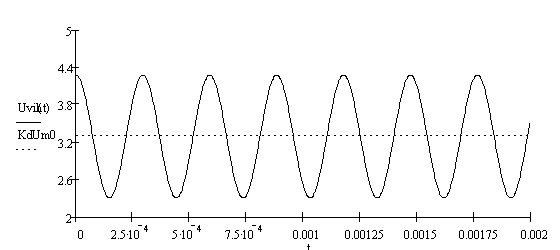
Рисунок 3.2 - График сигнала на выходе детектора.

Изобразим ВАХ диода, а также временные диаграммы тока диода и напряжения на диоде:

Рисунок 3.3 – График ВАХ диода, временные диаграммы тока диода и напряжения на диоде

Задание №4

Генератор на полевом транзисторе с контуром в цепи стока генерирует гармоническое колебание с частотой . Контур состоит из индуктивности L, емкость C и имеет добротность Q. Крутизна сток-затворной характеристики транзистора в рабочей точке S.

Условие:

1. Изобразить электрическую схему генератора. Записать дифференциальное уравнение и вывести условие самовозбуждения генератора.

2. Определить критические коэффициенты включения .

3. Выбрать значение P, обеспечивающее устойчивую генерацию и рассчитать неизвестный элемент контура.

4. Изобразить качественно процесс установления колебаний в генераторе, указать области нестационарного и стационарного режимов.

Исходные данные:

Индуктивная трехточечная схема;

Решение:

1. Представим принципиальную схему индуктивного трехточечного автогенератора [2]:

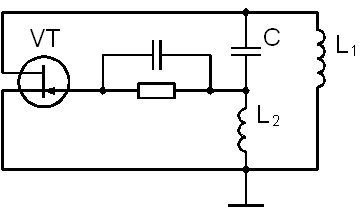
Рисунок 4.1 – Автогенератор, собранный по индуктивной трехточечной схеме.

Для составления дифференциального уравнения генератора рассмотрим колебательный контур подробнее, при этом как бы разорвав обратную связь (рисунок 4.2).

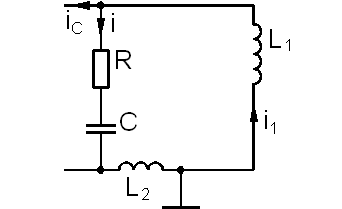
Рисунок 4.2 – Колебательный контур автогенератора.

В схеме на рисунке 4.2 R – сопротивление потерь контура.

По законам Кирхгофа и, используя компонентные уравнения элементов запишем систему характеристических уравнений [6] цепи представленной на рисунке 4.2.

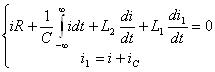. (4.1)

Для решения системы (4.1) не хватает еще одного уравнения. Его мы возьмем воспользовавшись характеристиками транзистора:

. (4.2)

Теперь проведя необходимые подстановки запишем уравнение с одним неизвестным током i.

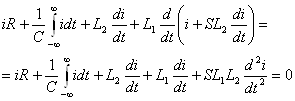. (4.3)

Чтобы избавиться от интеграла продифференцируем уравнение (4.3) по времени.

. (4.4)

Обозначим коэффициенты при неизвестном и его производных, как и соответственно при дифференциалах 0-ого, 1-ого, 2-ого и 3-его порядков. Тогда (4.4) примет вид:

. (4.5)

Для определения условия самовозбуждения воспользуемся критерием устойчивости Рауса-Гурвица [2]. В соответствии с этим критерием, для самовозбуждения необходимо и достаточно чтобы выполнялось:

1) 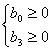; (4.6)

2) . (4.7)

Подставляя значения коэффициентов , получим условие самовозбуждения автогенератора.

. (4.8)

2. Определим критические коэффициенты включения индуктивности. Для этого проведем в (4.8) некоторые преобразования.

Поскольку индуктивность не отрицательна и не равна 0, то разделим (4.8) на нее.

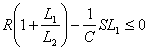. (4.9)

Введем величину коэффициента включения индуктивности р:

. (4.10)

Где - полная индуктивность контура. (4.11)

Исходя из (4.10) и (4.11) можно записать:

. (4.12)

Подставим (4.12) в (4.9).

. (4.13)

Как известно - характеристическое сопротивление контура. Т.о. неравенство (4.13) примет вид:

. (4.14)

Разделив (4.14) на получим:

, (4.15)

но это есть добротность контура Q.

. (4.16)

Теперь если учесть, что (4.15), а затем умножить неравенство на , получим окончательное уравнение для вычисления критических коэффициентов включения.

. (4.17)

Используя [3] определим критический коэффициент включения индуктивности:

3. Рассчитаем неизвестный элемент контура (в нашем случае это индуктивность) по следующей формуле:

(4.18)

Подставив исходные данные, получим:

Определим коэффициент усиления усилителя:

Найдём значения индуктивностей L1 и L2 при помощи [3], используя операцию Given:

4. Представим качественный график процесса установления колебаний в автогенераторе (рисунок 4.3):

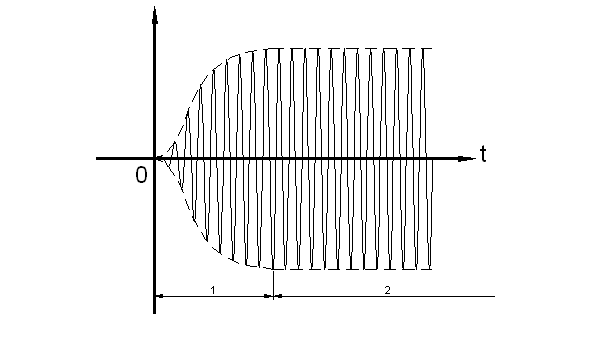Рисунок 4.3 – Процесс установления автоколебаний:

1. Нестационарный режим – режим, при котором параметры колебания меняются.

2. Стационарный режим – режим, при котором параметры колебания не меняются.

Задание №5.

Условие:

Аналоговый сигнал S(t) (рисунок 5.1) длительностью подвергнут дискретизации путем умножения на последовательность - импульсов. Интервал дискретизации Т.

Требуется:

1. Рассчитать спектр аналогового сигнала S(t) и построить график модуля спектральной плотности.

2. Определить максимальную частоту в спектре аналогового сигнала , ограничив спектр, использовав один из критериев.

3. Рассчитать интервал дискретизации Т и количество выборок N. Изобразить дискретный сигнал под аналоговым в том же временном масштабе.

4. Определить спектральную плотность дискретного сигнала и построить график модуля под графиком спектра аналогового сигнала и в том же частотном масштабе.

5. Провести дискретное преобразование Фурье (ДПФ), определить коэффициенты ДПФ и построить спектрограмму модуля этих коэффициентов под графиками спектров аналогового и дискретного сигналов и в том же частотном масштабе.

Записать выражение для Z - преобразования дискретного сигнала.

Решение:

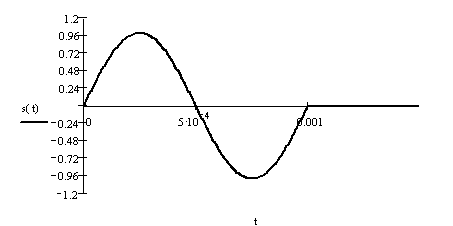
Рисунок 5.1 – график исходного сигнала

1.Рассчитаем спектр аналогового сигнала S(t), данный сигнал представляет собой ни четную ни нечетную функцию. Зададим сигнал S(t) аналитически:

(5.1)

Спектральная плотность рассчитывается путем прямого преобразования Фурье [7]:

. (5.2)

где (5.3)

Где и весовые коэффициенты. Подставляя значения с помощью [3] построим график спектральной плотности (рисунок 5.2).

Рисунок 5.2 – график модуля спектральной плотности

2. Определим максимальную частоту в спектре аналогового сигнала по уровню 0,1.

(5.4) 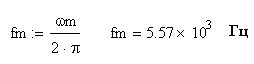. (5.5)

3. Условие выбора интервала дискретизации возьмем из теоремы Котельникова :

. (5.6)

Подставив значения, получим:

Воспользовавшись (5.6) выберем интервал дискретизации:

В этом случае количество выборок определяется следующим образом:

. (5.7)

N = 21;

Теперь, когда мы нашли интервал дискретизации и количество выборок построим график дискретного сигнала, а так же для сравнения в одном масштабе с ним график аналогового (рисунок 5.3):

Рисунок 5.3 – Графики: а) аналогового сигнала;

б) дискретного сигнала.

На рисунке 5.3 в величине выборок отражен весовой коэффициент δ - импульсов дискретизации.

4. Спектр дискретного сигнала, как известно, представляет собой сумму копий спектральных плоскостей исходного аналогового сигнала, подвергнутого дискретизации, сдвинутых на величину частоты следования выборок друг относительно друга [7].

Т. о. Формула спектральной плотности дискретного сигнала примет вид:

. (5.8)

Пользуясь (5.8) построим график при помощи [3]:

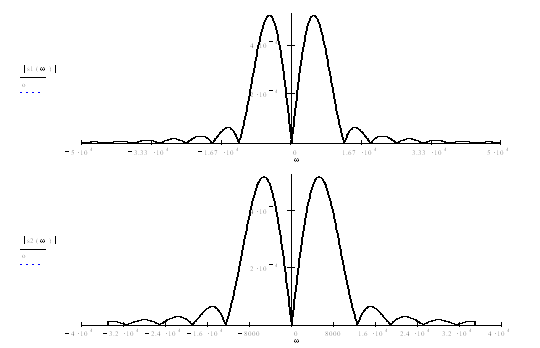
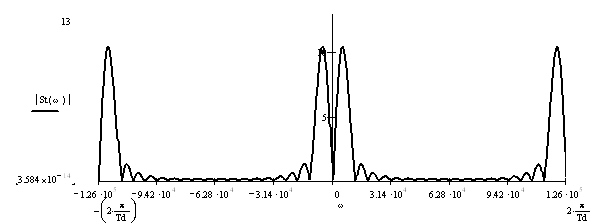
Рисунок 5.4 – а) модуль спектральной плотности аналогового сигнала; б) ограниченный спектр аналогового сигнала;

в) спектральная плотность дискретного сигнала;

5. Дискретное преобразование Фурье определяется формулой (5.9) [2]:

. (5.9)

Где: - номер отсчета спектральной плотности; ;

- номер отсчета дискретного сигнала; .

Т. о. по формуле (5.9) и при помощи [3] можно подсчитать значения дискретных отсчетов:

Зная, что выше вычисленные отсчеты следуют через интервалы , величина которых определяется следующим соотношением [2]:

, (5.10)

где: N – количество выборок дискретного сигнала;

Т – период дискретизации;

можно построить спектрограмму модулей этих коэффициентов.

Данную спектрограмму будем строить в одном частотном масштабе с графиками спектров аналогового и дискретного сигналов и расположив ее под ними.

Рисунок 5.5 – а) Спектр аналогового сигнала;

б) Спектральная плотность дискретного сигнала;

в) Спектрограмма модулей коэффициентов ДПФ.

6. Заменив в формуле (5.9) на Z (в данном случае играет роль частоты) прейдем к выражению для Z-преобразования.

. (5.11)

Распишем (5.11) подробнее, при этом заметим, что как видно из рисунка 5.3 отсчеты с номерами от 0 до 8 равны 1, а 9 равен 0. С учетом всего сказанного получим:

. (5.12)

При помощи простых математических преобразований представим (5.12) в виде дробно-рационального выражения:

. (5.13)

Задание №6.

Условие:

Уравнения цифровой фильтрации имеют вид:

(6.1)

Требуется:

1. Составить структурную схему фильтра.

2. Найти передаточную функцию фильтра. Определить полюса передаточной функции и нанести их на - плоскости. Сделать вывод об устойчивости.

3. Рассчитать и построить АЧХ и ФЧХ фильтра.

4. Найти системную функцию фильтра. Определить полюса системной функции и нанести их на - плоскости. Сделать вывод об устойчивости.

5. Рассчитать и построить импульсную характеристику фильтра.

6. Рассчитать и построить выходной сигнал цифрового фильтра, если на вход подаётся дискретный сигнал из задания 5.

Исходные данные:

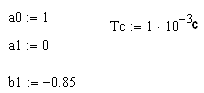
Решение:

1. Данный фильтр реализовывается с помощью рекурсивного фильтра 1-го порядка. Схема данного фильтра представлена на рисунке 6.1:

Рисунок 6.1 - Рекурсивный фильтр

2. Передаточная функция цифрового фильтра имеет вид:

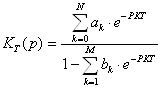, (6.2)

где ак, bk коэффициенты уравнения; - интервал дискретизации; - количество элементов задержки в трансверсальной части; - количество элементов задержки в рекурсивной части.

Найдём полюса передаточной функции с помощью формулы:

(6.3)

Для нахождения полюсов воспользуемся [3]:

Для обеспечения устойчивости необходимо и достаточно, чтобы полюса передаточной функции находились в левой полуплоскости комплексного переменного p. Поскольку

- система устойчива.

3. С помощью [3] рассчитаем и построим АЧХ и ФЧХ фильтра:

(6.4)

Для данной передаточной функции с помощью [3] построим АЧХ и ФЧХ фильтра (рисунок 6.2):

Рисунок 6.2 - а) АЧХ фильтра; б) ФЧХ фильтра.

4. Найдем системную функцию фильтра путем замены ePT на Z. Системная функция будет иметь вид:

(6.5)

Устойчивость фильтра оценивается расположением полюсов системной функции на z плоскости. Фильтр устойчив, если полюса системной функции расположены внутри круга единичного радиуса с центром в точке .

Определим полюса системной функции в плоскости Z с помощью [3]:

- т.е. система устойчива.

5. Импульсная характеристика - это реакция цифрового фильтра на воздействие в виде единичного импульса (функция Кронекера). Используя уравнение цифровой фильтрации, получаем:

(6.6)

где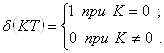

Для данного фильтра импульсная характеристика будет определятся формулой:

(6.7)

График импульсной характеристики представлен на рисунке 6.4:

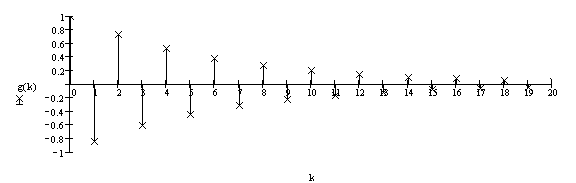
Рисунок 6.4.-Импульсная характеристика.

6. Графики входного дискретного сигнала и выходного цифрового сигнала (рисунок6.3):

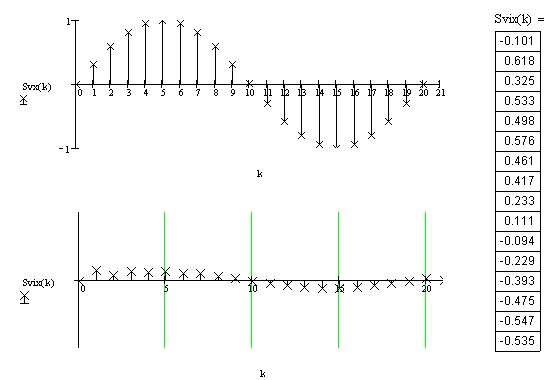
Рисунок 6.3 - а) входной дискретный сигнал; б) выходной цифровой сигнал.

Задание №7

Условие:

Синтезировать согласованный фильтр для данного сигнала.

Требуется:

1. Определить комплексный коэффициент передачи фильтра.

2. Синтезировать структурную схему фильтра.

3. Определить и построить выходной сигнал (под входным).

4. Оценить отношение сигнал/помеха на выходе в зависимости от .

Исходные данные:

Когерентная пачка из радиоимпульсов с прямоугольной огибающей и скважностью равной ,

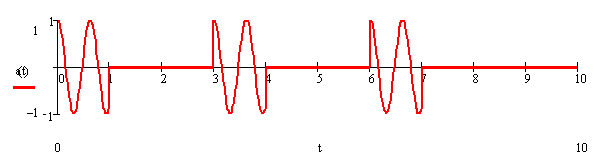
Рисунок 7.1 – Входной сигнал

Решение:

1. Синтезировать согласованный фильтр удобно при помощи его комплексного коэффициента передачи. Запишем общую формулу для его определения [2]:

. (7.1)

Где - постоянный коэффициент;

- функция, комплексно сопряженная со спектральной плотностью входного сигнала;

- время задержки пика выходного сигнала.

Для существует ограничение - , это связано с физическими принципами работы согласованного фильтра [2]. Однако обычно полагают:

. (7.2)

Из формулы (7.1) видно, что задача сводится к определению спектральной плотности входного сигнала. Для ее определения разобьем входной сигнал на отдельные импульсы, затем определим спектр одного из них, а результат запишем в виде суммы вышеопределенных спектральных плотностей всех составляющих пачки, но сдвинутых по времени на расстояния кратные периоду их следования.

Итак, определим - спектр одиночного радиоимпульса, путем применения свойства [2], в котором говорится, что спектр радиосигнала это есть спектр его огибающей только сдвинутый в область высоких частот (окрестность ).

. (7.3)

Где - спектральная плотность для огибающей одиночного радиоимпульса, смещенная в область ВЧ на .

Запишем аналитическое выражение для огибающей радиоимпульса:

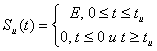. (7.4)

Определим , для этого применим прямое преобразование Фурье [7].

;

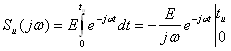. (7.5)

Представим формулу для , заменив в (7.5) на :

. (7.6)

Т. о. спектральная плотность всей пачки импульсов будет определяться как сумма спектральных плотностей определяемых формулой (7.6), но сдвинутых друг относительно друга на:

. (7.7)

Представим это соотношение, применив теорему сдвига [2]:

. (7.8)

Запишем формулу комплексно сопряженной спектральной плотности входного сигнала, преобразовав (7.8), путем перемены знака мнимой части.

. (7.9)

Подставим (7.6) в (7.9), а полученный результат в (7.1) и проведем некоторые преобразования для удобства ее дальнейшего использования:

(7.10)

2. Т. о. согласованный фильтр можно представить как каскадное соединение двух блоков:

1. согласованный фильтр одиночного радиоимпульса;

2. т. н. синхронный накопитель (многоотводная линия задержки).

Схема такого фильтра представлена на рисунке 7.2.

2Т

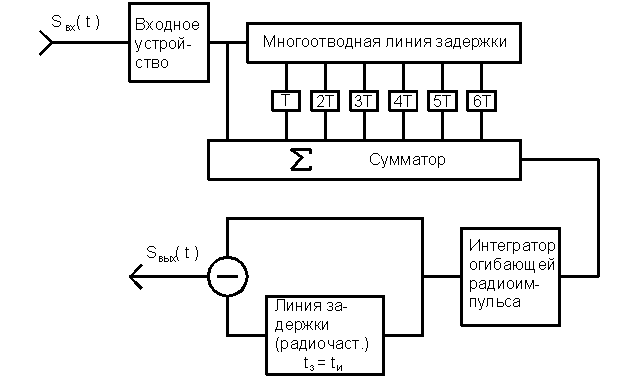
Рисунок 7.2 – Структурная схема согласованного фильтра для сигнала представленного на рис. 7.1.

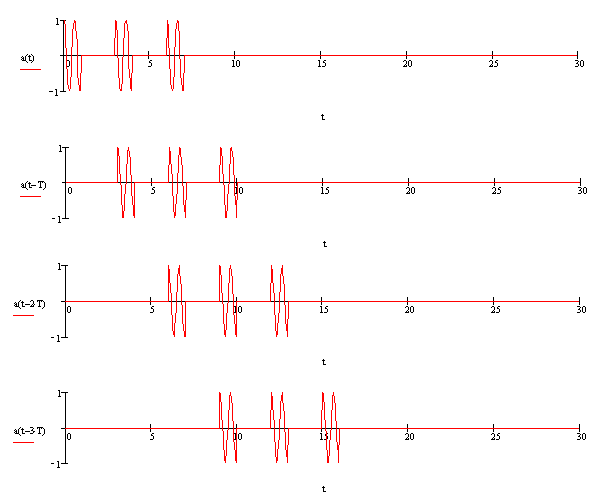
График когерентной пачки радиоимпульсов проходящей через линию задержки представлен на рисунке (7.3).

Рисунок 7.3 - График пачки радиоимпульсов, проходящих через линию задержки

Сигнал на выходе согласованного фильтра с точностью до константы совпадает с автокорреляционной функцией входного сигнала, сдвинутой на в сторону запаздывания [2].

АКФ пачки радиоимпульсов с прямоугольной огибающей представляет собой последовательность треугольных импульсов длительностью и максимумом равным , где n –количество импульсов пачки, Э1 – полная энергия одного импульса (максимум АКФ одиночного импульса).

Для начала рассчитаем АКФ одиночного радиоимпульса.

Как известно АКФ радиосигнала равна произведению АКФ огибающей на АКФ несущей [1]:

. (7.11)

Поскольку АКФ несущего колебания есть само это колебание нулевой начальной фазой и амплитудой равной 1, то можно записать:

. (7.12)

Рассчитаем АКФ огибающей :

. (7.13)

Подставим (7.13) в (7.12):

. (7.14)

3. При помощи (7.14) и приведенных выше условий с помощью [3] построим график выходного сигнала и АКФ (рисунок 7.4):

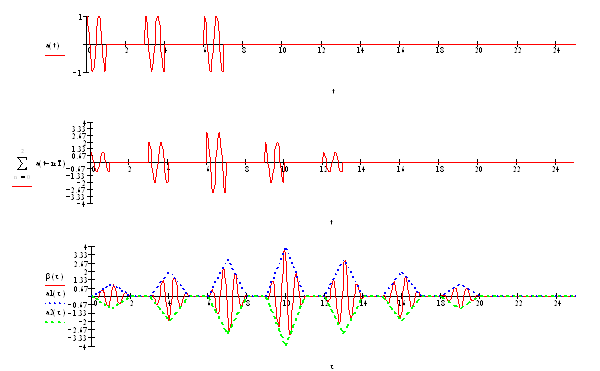Рисунок 7.4 –а) входной сигнал, б) сигнал на выходе согласованного фильтра; в)АКФ сигнала

4. Отношение сигнал/помеха на выходе согласованного фильтра равно:

. (7.15)

Где Э – полная энергия входного сигнала;

W0 – спектральная плотность мощности белого шума на входе фильтра.

Величина полной энергии входного сигнала с точностью до константы совпадает со значением выходного сигнала при (по свойствам АКФ).

. (7.16)

Из формул (7.15) и (7.16) видно, что при увеличении n – количества и скважности импульсов пачки входного сигнала соотношение сигнал/помеха на выходе фильтра увеличивается, что соответствует теории поскольку при этом растет база сигнала. Однако данный способ повышения выигрыша по величине отношения не улучшает корреляционных свойств сигнала, из-за чего через пороговое устройство может проходить не один, а несколько импульсов и отметок на экране индикаторного устройства так же будет несколько. Т. о. кроме увеличения базы сигнала необходимо еще и улучшать его корреляционные свойства.

ПЕРЕЧЕНЬ ССЫЛОК

1. Гармаш М. А. Конспект лекций по дисциплине СиПРТ (1,2 часть).

2. Гоноровский И.С. Радиотехнические цепи и сигналы: Учебник для вузов.4-е издание, перераб. и доп.-М.:Радио и связь,1986.- 512с.

3. Математический пакет MathCAD 2000.

4. Гимпилевич Ю.Б., Афонин И.Л. методические указания к выполнению курсовой работы по дисциплине СиПРТ для студентов специальности 7.090701-“Радиотехника” (дневная форма обучения).