Шпаргалка: Основы гидрогазодинамики

Шпаргалка: Основы гидрогазодинамики

Экзаменационные вопросы по курсу «Гидрогазодинамика»

1. Силы, действующие в жидкости

2. Методы изучения движения жидкости

3. Траектория, линия тока, трубка тока, струя

4. Градиент, дивергенция, циркуляция, вихрь

5. Основная теорема кинематики (первая теорема Гельмгольца)

6. Тензор скоростей деформации

7. Уравнение сплошности

8. Нормальное и касательное напряжение, действующие в движущейся жидкости

9. Уравнение движения сплошной среды в напряжениях

10. Напряжения, действующие в идеальной жидкости

11. Уравнение движения идеальной жидкости (Эйлера)

12. Уравнение движения идеальной жидкости (Эйлера) в форме Громека

13. Теорема Бернулли

14. Основные понятия и определения потенциальных течений

15. Комплексный потенциал, комплексная скорость

16. Частные случаи плоских потенциальных течений

17. Безциркуляционное обтекание круглого цилиндра

18. Обобщенный закон Ньютона

19. Уравнения движения вязкой несжимаемой жидкости (Навье-Стокса)

20. Подобие гидродинамических явлений

21. Критериальные уравнения. Критерии и числа подобия

22. Моделирование ГГД явлений

23. Ламинарное и турбулентное движение

24. Пограничный слой и его характерные толщины

25. Переход ламинарного ПС в турбулентный

1. Силы, действующие в жидкости

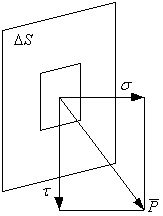
В жидкостях могут существовать только распределенные силы: массовые (объемные) и поверхностные.

1) Массовые силы действуют на каждую точку выделенного объема τ и пропорциональны массе частиц. Например, сила тяжести, центробежное ускорение, сила электростатического напряжения, сила Кориолиса и т.д.

Массовые силы характеризуются вектором плотности массовых сил:

 ,

который представляет собой предел отношения главного вектора массовых сил к массе частицы при стремлении массы к нулю.

В проекциях на координатные оси он может быть записан:

X, Y, Z – проекции  на координатные оси.

2) Поверхностные силы характеризуются напряжениями:

- это предел отношения главного вектора поверхностной силы, приложенного к  и величине этой площадки при стремлении ее к нулю. Величина напряжения зависит от выбора направления площадки.

- нормальное напряжение

 - касательное напряжение

2. Методы изучения движения жидкости

Существует два метода изучения движения жидкости: метод Эйлера и метод Лагранжа.

1. Метод Лагранжа: выделяется частица в движущейся жидкости и исследуется ее траектория в зависимости от координат и времени.

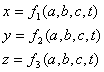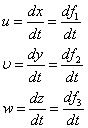(1)                         (2)

a, b, c – это постоянные, которые определяют положение точки в начальный момент времени.

2. Метод Эйлера: задается метод распределения скорости в потоке в зависимости от координат и времени:

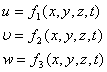(3)

x, y, z –переменные Эйлера.

Чтобы определить скорости в какой-либо точке надо задать ее координаты. Поле ускорений потока можно получить если продифференцировать систему (3):

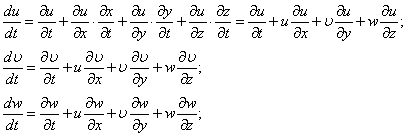
Получили систему, описывающую поле ускорений.

Локальные ускорения, показывающие как изменяется скорость в какой-либо точке потока с течением времени ().

Конвективные ускорения (все остальное в правой части), связанные с перемещением точки или среды (т.е. с конвекцией). Течение может быть стационарным или нестационарным (изменяется во времени). Для стационарных задач локальные ускорения равны нулю. Самые простые течения стационарные, плоские и одномерные. Для стационарной и плоской задачи исследуется течение только по двум координатам. Еслирассматривается одномерная стационарная задача, тогда:

3. Траектория, линия тока, трубка тока, струя

Траектория – это линия, изображающая путь пройденный частицей за определенный промежуток времени.

Линия тока – это мгновенная векторная линия, в каждой точке которой в данный момент времени касательная по направлению совпадает с вектором скорости.

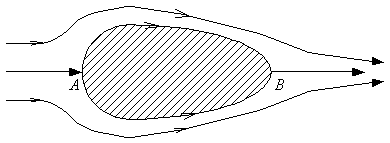
В стационарных задачах линии тока и траектории совпадают, т.к. нормальная составляющая скорости к линии тока равна нулю, жидкость через линию тока не перетекает. В плоских течениях количество жидкости между двумя линиями тока в любых сечениях будет одинаково. Если линии тока приближаются, то скорость потока увеличивается, и наоборот. Через каждую точку в потоке можно провести только одну линию тока, исключение составляют особые точки: критические точки. А и В – это критические точки. Поверхность непроницаемого тела – поверхность тока, а линии тока, расположенные на поверхности называется нулевыми линиями тока.

Если в жидкости провести замкнутый контур и через каждую точку провести линию тока, получим поверхность тока. Жидкость внутри поверхности называется трубкой тока. Через поверхность тока жидкость не перетекает, следовательно через каждое сечение трубки тока проходит одно и то же количество жидкости. Если через каждую точку контура провести траекторию, то часть жидкости, которая ограничена поверхностью траектории называется струей. Струя совпадает с трубкой тока в стационарном течении.

4. Градиент, дивергенция, циркуляция, вихрь

1. Градиент.

Рассмотрим действие векторного оператора Гамильтона на скалярную функцию φ. Скалярная величина – это параметр, которому нельзя придать направление.

Градиент скалярной функции – это вектор направленный по нормали к линии постоянного значения в сторону возрастания функции и модуль его равен частной производной от функции по направлению указанной нормали.

2. Дивергенция.

Рассмотрим скалярное умножение векторного оператора и двух величин скорости:

Дивергенция является скалярной величиной, показывает расхождение вектора скорости, определяет закон относительного изменения объема. Например, если течение стационарное и жидкость несжимаемая, то при  в жидкости отсутствуют источники или стоки. При  имеется источник, при  имеется сток. Уравнение  часто используется для замыкания системы уравнений движения несжимаемой жидкости и является уравнением сплошности.

3. Циркуляция.

Характеризует интенсивность вращательного движения жидкости.

Вычисляется, например, по контуру АВ:

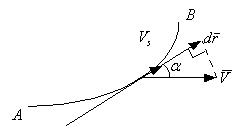
- элемент контура АВ

4. Вихрь вектора скорости.

Рассмотрим векторное произведение оператора на вектор скорости:

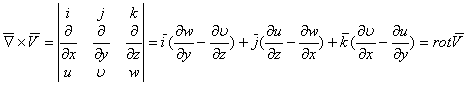
Рассмотрим вращение точки вокруг оси, проходящей через начало координат с угловой скоростью .

Если в жидкости , это указывает на наличие вращающихся объемов, вихрей жидкости. Интерес представляют течения для которых , такие течения называются безвихревыми или потенциальными,. Т.к. в этом случает существует потенциал вектора скорости φ, который связан с составляющими вектора скорости следующими соотношениями:

; ; ;

5. Основная теорема кинематики (первая теорема Гельмгольца)

Из теоретической механики известно, что скорость движения любой точки твердого тела складывается из поступательного вместе с некоторым полюсом и вращательного движения вокруг оси, проходящей через этот полюс: . Для жидкой частицы основная теорема кинематики гласит, что скорость движения любой точки жидкой частицы складывается из скорости квазитвердого движения и деформационного. Квазитвердое состоит из поступательного вращательного: . Для доказательства рассмотрим движение точки М с координатами x, y, z, которая находится в окрестности точки М0 (x0, y0, z0) и составляющая для точки М0 скорости (u0, υ0, w0), тогда раскладывая функцию скорости в ряд Тейлора и сохраняя компоненты первого порядка малости, составляющие скорости для точки М можно записать:

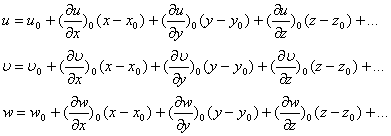
Преобразуем первое уравнение. Для этого разноименные части представим следующим образом:

;

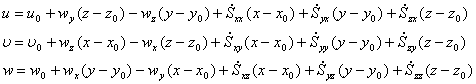
- первая теорема Гельмгольца квазитвердое движение деформационное движение

6. Тензор скоростей деформации

Компоненты , входящие в скорость деформации, могут быть представлены в виде матрицы, которая называется тензором скоростей деформации:

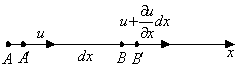
 - диагональные компоненты.

Тензор симметричен относительно главной диагонали

Рассмотрим диагональные компоненты. В жидкости выделим отрезок АВ длиной dx (отрезок на оси х). Рассмотрим перемещение отрезка вдоль оси х. Скорости в точках А и В не равны. Через время dt отрезок займет положение . Произошла линейная деформация отрезка АВ на величину:

Если разделим линейную деформацию на длину отрезка:

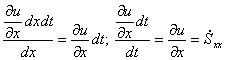
скорость линейной деформации – скорость растяжения или сжатия линейного отрезка расположенного на оси х в направлении оси х. Аналогично:

скорости относительных линейных деформаций вдоль соответствующих осей. Сумма диагональных компонент определяет дивергенцию вектора скорости, т.е.

закон относительного изменения объема.

Рассмотрим перемещение отрезка АВ расположенного на оси х и длиной dx в направлении оси dy).

Ввиду малости угла

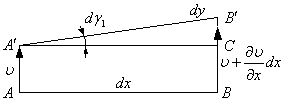
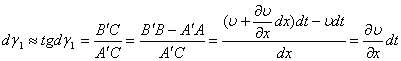
угловая деформация линейного отрезка в направлении оси у.

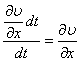
скорость угловой деформации или скорость скашивания в направлении оси у. Если отрезок расположить на оси у, то  - скорость скашивания в направлении оси х. - средняя скорость угловой деформации в плоскости ху.

Таким образом недиагональные компоненты характеризуют скорости скашивания или угловых деформаций в соответствующих плоскостях.

7. Уравнение сплошности

Уравнение сплошности – это уравнение закона сохранения массы:

Выделим в жидкости элементарный объем  с плотностью ρ.

Следовательно:

Второй член полученного уравнения выражает закон относительного изменения объема,. Т.е. дивергенцию.

Плотность в общем случае зависит от координат и времени:

Поэтому:

уравнение сплошности (неразрывности).

Если течение стационарное, то уравнение упрощается:

Если жидкость несжимаемая, т.е. , то

8. Нормальное и касательное напряжение, действующие в движущейся жидкости

Закон сохранения количества движения для неизолированной системы может быть записан в виде:

где  - главный вектор количества движения системы

 - главный вектор внешних сил, действующих на систему

В жидкости выделим элементарный тетраэдр с гранями , , , . Индекс показывает перпендикулярно какой оси расположены грани,  - наклонная грань. К граням приложены соответствующие напряжения , , ,  (не перпендикулярные граням). Масса тетраэдра . На тетраэдр действуют массовые и поверхностные силы. Массовые характеризуются вектором плотности , поверхностные – напряжениями.

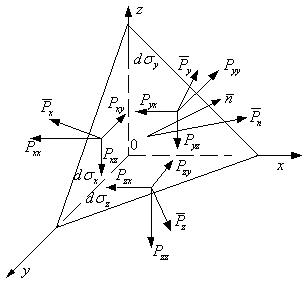
 - скорость центра инерции тетраэдра

 - третий порядок малости

 - второй порядок малости

Членами третьего порядка малости пренебрегаем.

 и т.д.

            пх

Получим связь напряжений, действующих на грани выделенного тетраэдра:

В проекциях на координатные оси это уравнение может быть переписано:

В записанной системе  называются нормальными напряжениями, а  и т.д. называются касательными напряжениями. Все напряжения могут быть записаны в матричной форме в виде симметричного тензора напряжений:

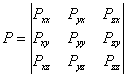
Первый индекс определяет ось, относительно которой расположена грань, второй – ось на которую проецируется напряжение.

9. Уравнение движения сплошной среды в напряжениях

Рассмотрим элементарный параллелепипед с ребрами . Объем его . На него действуют массовые и поверхностные силы определяемые главным вектором внешних сил . К параллелепипеду применим закон сохранения количества движения:

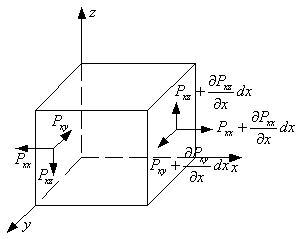
Для определения главного вектора поверхностных сил рассмотрим все силы, дающие проекцию на ось х. Для граней перпендикулярных х проекцию дают только силы, создаваемые нормальными напряжениями. Поэтому равнодействующая этих сил равна:

Аналогично для граней перпендикулярных z получим равнодействующую равную:

Равнодействующая поверхностных сил в проекции на ось х равна:

Тогда закон сохранения количества движения в проекции на х можно записать:

Полученная система называется системой уравнений движения сплошной среды в напряжениях. В левой части стоит полная производная от скоростей, которые могут быть расписаны через локальные и конвективные составляющие ускорения. При определенных условиях левая часть значительно упрощается (стационарное, двухмерное или одномерное течение).

Т.к.

систему можно записать в виде одного уравнения в векторной форме записи:

10. Напряжения, действующие в идеальной жидкости

В идеальной жидкости отсутствуют силы трения, следовательно касательные напряжения равны нулю. Применительно к элементарному тетраэдру проекция напряжения, приложенного к произвольной наклонной грани на ось х равна:

С другой стороны:

Аналогично для проекций на у:

 и

Таким образом в идеальной жидкости величина нормального напряжения в любой точке не зависит от направления площадки к которой напряжение приложено. В идеальной жидкости величина нормального напряжения в точке называется гидродинамическим давлением в этой точке. Модель идеальной жидкости упростила постановку и решение многих задач, в которых влиянием сил трения можно пренебречь.

Знак «минус» ставится, т.к. жидкость оказывает давление на выделенный объем в направлении противоположном внешней нормали.

11. Уравнение движения идеальной жидкости (Эйлера)

Для вывода воспользуемся уравнениями движения в напряжениях:

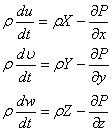 - система уравнения Эйлера для идеальной жидкости.

Справедлива, как для сжимаемой, так и для несжимаемой жидкости. Если жидкость сжимаемая, то необходимо ввести функцию координаты от времени:  

Если жидкость несжимаемая, то

12. Уравнение движения идеальной жидкости (Эйлера) в форме Громека

Все преобразования выполним на первом уравнении:

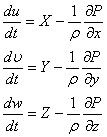
Отсюда:

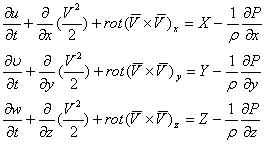
- система уравнений движения для и.ж. в форме Громека

Рассмотрим далее движение, предполагая, что массовая сила имеет потенциал и течение баротропное.

Первое предположение утверждает, что у массовых сил имеется потенциал, связанный соотношениями с массовыми силами:

; ; ,

U - потенциал массовых сил.

Второе: баротропным считается течение, у которого ρ считается только функцией давления.

Например, баротропными течением является:

1)  ρ=const – газ или жидкость несжимаемы

2)  движение среды изотермическое -

3)  движение среды адиабатное -

Условие баротропности предполагает, что существует некоторая функция Р, зависящая от давления, которая определяется выражением:

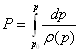
Функция Р связана с р и ρ соотношениями:

; ; .

Подставим в систему уравнений Громека потенциал массовых сил и функцию Р:

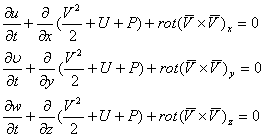
 - система уравнений Эйлера в форме Громека

Достоинство системы заключается в том, что отдельно выделен ротор, который при определенных условиях может быть равен нулю и система значительно упрощается. Последний член равен нулю, если: 1)  - статическая задача; 2)  - течение безвихревое или потенциальное.

Сумма, стоящая во второй компоненте, имеет определенный физический смысл. В векторной форме система может быть записана в виде одного уравнения:

13. Теорема Бернулли

Рассмотрим стационарное баротропное течение под действием массовых сил, т.е. можно записать:

умножим уравнение скалярно на вектор скорости, тогда последний член равен нулю, т.к. идет скалярное перемножение перпендикулярных векторов.

 - единичный вектор в направлении вектора скорости. Вектор скорости направлен по касательной к линии тока или к траектории, т.к. течение стационарное, следовательно:

- производная по направлению.

выражение отражает теорему Бернулли: при стационарном баротропном течении идеальной жидкости под действием потенциальных массовых сил сумма кинетической энергии единицы объема, функции давления приведенного к единице массы потенциала массовых сил сохраняет постоянное значение вдоль любой линии тока.

Если бы скалярно умножили исходное уравнение на вектор угловой скорости, то получили бы аналогичный результат вдоль вихревой линии.

Если течение потенциальное, то  и сразу же получается:

и  

во всем потоке, т.е. трехчлен Бернулли сохраняет постоянное значение во всей области потенциального потока.

Рассмотрим потенциальное течение несжимаемой жидкости под действием сил тяжести. Т.к. жидкость несжимаема то :

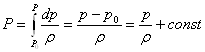
У сил тяжести потенциал равен: , z – координата.

  (1),  - удельный вес

Все эти составляющие имеют размерность давления и называются напорами: - скоростной или динамический напор; р – пьезометрический напор;  - геометрический напор; ро – полный напор

При стационарном течении идеальной несжимаемой жидкости полный напор, равный сумме , сохраняет постоянное значение вдоль любой линии тока, а при потенциальном течении во всей области потока.

В задачах, в которых можно пренебречь влиянием геометрического напора, уравнение Бернулли упрощается и приобретает вид:

Уравнение (1) разделим на , тогда:

все компоненты измеряются в метрах и называются высотами:  - скоростная высота,  - пьезометрическая высота, z – нивелирная высота, Н – гидравлическая высота. При стационарном движении идеальной несжимаемой жидкости высота

сохраняет постоянное значение вдоль любой линии тока (или вихревой линии), а при потенциальном течении во всем токе.

14. Основные понятия и определения потенциальных течений

Потенциальные течения – это течения, у которых во всем потоке, следовательно существует функция φ, называемая потенциалом, зависит φ(х,у,z,t) и связана с составляющими U соотношениями:

 то есть

Записанные соотношения могут быть записаны и для любой другой функции, которая отличается от φ на константу: . Таким образом, уравнение потенциала определяется с точностью до константы. Геометрическое место точек с одинаковым значением φ образуют эквипотенциальные поверхности, уравнения которых: . Так как , следовательно вектор U расположен по перпендикулярам в любой точке эквипотенциальной поверхности. Так как вектор U касателен к линии тока, то линии тока перпендикулярны эквипотенциальной поверхности.

Рассмотрим стационарное плоское течение, то есть , тогда

и .

Уравнение сплошности имеет вид:

Таким образом, потенциал U удовлетворяет уравнению Лапласа, следовательно является гармонической функцией.

Введем в рассмотрение функцию ψ, связанную с составляющими U уравнениями:

и

Функция ψ удовлетворяет уравнению сплошности, т.к.

ψ – функция тока, она также определяется с точностью до постоянной.

Уравнение называется уравнением линии тока.

В плоских течениях эквипотенциальные поверхности дают проекции на плоскость (х,у) в виде линии, поэтому часто в задачах рассматриваются эквипотенциальные линии которые перпендикулярны линии тока.

В потенциальном потоке , в плоском течении

                          функция тока ψ гармоническая

Сравнение потенциала φ и ψ позволяет записать:

 -

условие Коши-Римана.

15. Комплексный потенциал, комплексная скорость

Из теории комплексной переменной известно, что если две функции φ и ψ, зависящие от х и у, удовлетворяют условиям Коши-Римана, то комплексная величина будет не просто зависеть, а являться функцией от комплексной переменной , то есть существует некоторая функция , действительной частью которой является φ, а мнимой ψ. .

Функция  имеет большое значение при изучении плоских потенциальных течений и называется комплексным потенциалом или характеристической функцией течения.

Так как  является аналитической функцией от , то ее производная не зависит от направления дифференцирования, а зависит только от положения точки в пространстве, то есть

по условию Коши-Римана:

Если вектор U разложить в комплексной плоскости годографа U, то .

Производная от комплексного потенциала дает зеркальное изображение комплексной U относительно действительной оси. Обозначим ее как

.

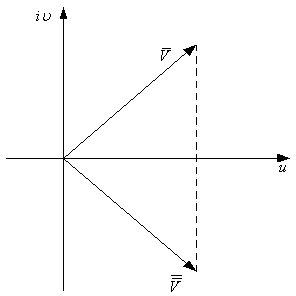
В теории комплексной переменной числа  и  называют сопряженными, назовем  как сопряженную U. Таким образом, производная от комплексного потенциала определяет .

Таким образом, если изменяется какое-то плоское потенциальное течение, то для него можно подобрать уравнение комплексного потенциала, проанализировать его и просчитать составляющие U в любой точке. С другой стороны для любого потенциала можно определить вид течения.

16. Частные случаи плоских потенциальных течений

1. Плоско параллельный поток:

Рассмотрим комплексный потенциал - , где а – действительное число

 и

- семейство прямых, параллельных оси у. - уравнение функции тока.

Линии тока - семейство прямых, параллельных оси х.  - уравнение эквипотенциальных поверхностей.

Для построения поля скоростей возьмем производные

;

Таким образом, рассмотренный потенциал описывает плоское течение потока вдоль оси х. Величину а можно рассматривать как скорость внешнего (набегающего) потока, .

2. Источник и сток.

Рассмотрим комплексный потенциал , а – действительное число (), тогда

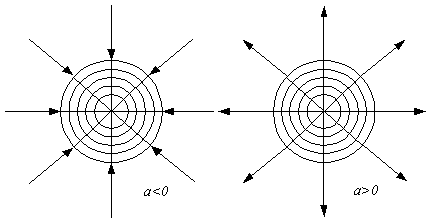
Уравнение для потенциала: .  - эквипотенциальные линии, семейство окружностей с центром в точке (0,0).

 - уравнение функций тока.  - семейство прямых, проходящих через точку (0,0).

Характер (вид) течения определяет знак при а. Если a>0, то это источник, если a<0, то это – сток.

 - объемный расход;

;  

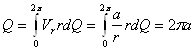
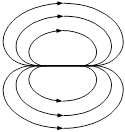
Если разместить источник и сток рядом то получится следующая картина.

Если их свести вместе, то получится диполь.

3. Рассмотрим комплексный потенциал:

Уравнение эквипотенциальных линий  - семейство окружностей, проходящих через точку (0,0) с центрами на оси х.

Уравнение для линий тока  - семейство окружностей, проходящих через точку (0,0) с центрами на оси у.

4. Рассмотрим комплексный потенциал вида:

Г – циркуляция вектора скорости – круговое течение потока.

- семейство прямых, проходящих через точку (0,0).

Это уравнение эквипотенциальных линий.

 - функция тока;

- линии тока – семейство окружностей с центром в (0,0).

 - радиальная скорость;

Исследованный потенциал определяет течение, которое называется потенциальным вихрем.

Окружная скорость изменяется по гиперболе.

17. Безциркуляционное обтекание круглого цилиндра

Рассмотрим комплексный потенциал, представленный в виде суммы двух, один из которых – поток плоскопараллельного течения, другой – диполя.

Если приравнять  к константе получим уравнение эквипотенциальной линии.  - линии тока,  - уравнение для нулевой линии тока. Если принять , то получим уравнение для нулевой линии тока:

Оно разделится на два: 1) у=0;

2)  - окружность с радиусом

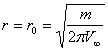
В идеальной жидкости трения нет, поэтому можно заменять любую линию тока, и характер течения не изменится, следовательно, если заменить нулевую линию тока твердой поверхностью, то получится задача обтекания цилиндра  плоским потоком. Представим функцию тока и потенциал в полярной системе координат:

 ; ;

Рассмотри составляющие скорости:

Значит: , то есть окружная составляющая скорости изменяется по синусоиде (при ,  - ). Точки А и В передняя и задняя критические точки соответственно.

Максимальные значения окружной скорости  при 90˚ и 270˚ - точки С и Д.

Нулевая линии тока проходит из (-∞) в передней критической точке А, раздваивается огибает цилиндр, соединяется в задней критической точке В и уходит в (+∞).

Для определения распределения давления по поверхности воспользуемся уравнением Бернулли:

Введем в рассмотрение коэффициент давления , показывающий безразмерное избыточное давление на поверхности:

На поверхности существует только окружная скорость, следовательно, для поверхности:

Из полученной формулы следует, что давление на поверхности максимально в критических точках А и В () и минимально в точках С и Д ().

Таким образом, распределение давлений симметрично относительно осей х и у. Результирующая сил давления на цилиндр равна нулю. Цилиндр не сносится потоком, его R=0.

Этот парадокс называется парадоксом Эйлера-Даламбера и присущ только для идеальной жидкости. Для реальных жидкостей обтекание цилиндра будет только при очень низких скоростях ().

Обычно обтекание цилиндра происходит с отрывами в задней части цилиндра, в результате, давление в лобовой зоне всегда больше, чем в кормовой.

Распределение давления описывается экспериментальными линиями, которые отличаются от теоретических. С увеличением скорости распределение давления стремится как бы к теоретическому, и

18. Обобщенный закон Ньютона

Ньютон установил связь напряжения трения между слоями движущейся жидкости с поперечным градиентом скорости

;

μ – коэффициент пропорциональности, называемый коэффициентом динамической вязкости.

 - коэффициент кинематической вязкости.

Касательное трение при движении потока вдоль оси х может быть записано в виде:

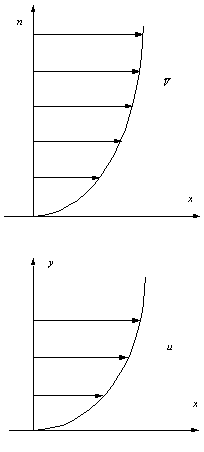
При движении потока вдоль оси у:

При движении потока в плоскости ху в произвольном направлении:

Записанные уравнения выражают обобщенный закон Ньютона для касательных напряжений. В скобках стоят величины, связанные с недиагональными компонентами тензора скоростей деформации. Они выражают скорости скашивания углов в соответствующих плоскостях. Таким образом касательные напряжения являются линейными функциями от скоростей скашивания углов в соответствующих плоскостях.

Определим нормальное напряжение вязкой жидкости. Если вязкость отсутствует, то нормальное напряжение не зависит от выбора направления площадки.

Нормальные напряжения вязкой жидкости выразим в виде суммы:

Компоненты, учитывающие вязкость связаны с диагональными компонентами тензора скоростей деформации соотношениями:

складываем

Среднее арифметическое нормальных напряжений, приложенных в точке в трех взаимно перпендикулярных направлениях, есть давление потока в этой точке:

обобщенный закон Ньютона для нормальных напряжений

Жидкости, которые подчиняются записанным уравнениям называются ньютоновскими жидкостями. Вязкие растворы, не подчиняющиеся уравнениям называются неньютоновскими, а раздел их изучающий – реология.

19. Уравнения движения вязкой несжимаемой жидкости (Навье-Стокса)

Рассмотрим изотермическое движение вязкой несжимаемой жидкости:

, .

В этом случае нормальные напряжения примут вид:

Уравнения движения получим из уравнения движения среды в напряжениях:

- система уравнений движения вязкой несжимаемой жидкости

Отличается от уравнений Эйлера тем, что в правой части появляется дополнительный член, который учитывает влияние сил вязкости.

Полученная система содержит 4 неизвестных . Для ее замыкания обычно используется уравнение сплошности. Полученная система может быть использована для решения бесконечного количества задач. Для перехода к конкретной задаче и ее решения, задачу необходимо описать с помощью условий однозначности. Условия однозначности состоят из четырех видов:

1)  геометрические условия – задается геометрия изучаемой системы (канала и т.д.)

2)  физические условия однозначности – задается вид движения жидкости и значения ее основных параметров .

3)  граничные условия – определяют условия течения на границе рассматриваемой системы. Часто в качестве граничных условий используют условия прилипания потока, т.е. скорость потока на поверхности равна 0. Скорость набегающего потока задается  или среднемассовая скорость  или скорость на границе пограничного слоя.

4)  Временные или начальные граничные условия задаются только для нестационарных задач и определяют особенности течения потока в начальный момент времени.

20. Подобие гидродинамических явлений

Решение системы Навье-Стокса даже для простых задач представляет значительную сложность, поэтому большое значение приобретает гидродинамический эксперимент, вопросы моделирования процесса. При моделировании необходимо учитывать влияние большого количества факторов на протекание процесса, чтобы полученные результаты на моделях можно было переносить на действующие образцы. Эту сложность в значительной степени позволяет устранить теория подобия, которая утверждает, что влияние отдельных факторов можно рассматривать в совокупности объединяя их в безразмерные комплексы – критерии подобия. Эти критерии получаются путем перевода размерных уравнений движения в безразмерные. Все критерии имеют определенный физический смысл. Анализ задачи приобретает следующие особенности: 1) уменьшается число переменных, т.к. количество критериев всегда меньше количества образующих их величин; 2) ярче выделяются физические особенности рассматриваемой задачи; 3)анализ приобретает обобщенный характер, т.к. одно и то же значение комплекса может быть получено путем бесконечного варьирования образующих величин.

Гидродинамические явления будут подобными если течения протекают в геометрически подобных системах. Наблюдается подобие полей скоростей и других важных физических характеристик. Константы пропорциональности называются константами подобия.

Выясним условия, при которых течения описываемые системой Навье-Стокса будут подобными. По геометрическим условиям однозначности должен быть задан какой-то характерный линейный размер:

1) ; 2) по физическим условиям однозначности должны быть определены ; 3) по граничным условиям должна быть определена ; 4) по начальным условиям задано характерное время , например период определяющий темп внешних воздействий

Таким образом в уравнениях зависимые переменные определяются как функции независимых переменных x, y, z, t и параметров задающих условие однозначности

Приведем уравнение движения к безразмерному виду методом масштабных преобразований. Будем относить физические величины к одномерным параметрам

; ;

В качестве масштаба для массовых сил примем ускорение свободного падения.

; ; ;

Выразим размерные величины через их масштабы в Уравнении Навье-Стокса:

Аналогично могут быть получены составляющие системы уравнений вдоль оси у и z.

Уравнение сплошности после приведения к безразмерному виду не изменится. После приведения уравнения движения к безразмерному виду появились безразмерные комплексы.

 - критерий динамической гомохронности;

 - критерий Фруда;

 - число Эйлера;  - критерий Рейнольдса.

После приведения уравнений к безразмерному виду изменился их физический смысл, т.к. один и тот же вид уравнений с подобными условиями будут соответствовать не единственному условию, а целой группе подобных явлений. В соответствии с теоремой подобия Кирпичева-Гухмана гидродинамические явления будут подобными если они: 1) описываются одной системой дифуравнений; 2) имеют подобные условия однозначности; 3) имеют численно равные критерии подобия

21. Критериальные уравнения. Критерии и числа подобия

После приведения уравнения Навье-Стокса к следующему виду они стали содержать следующие типы переменных: 1) безразмерные независимые переменные ; 2) безразмерные зависимые переменные ; 3) безразмерные критерии – комплексы, состоящие из величин заданных по условиям однозначности .

После приведения к безразмерному уравнению изменился характер уравнений. Уравнения приобрели обобщенный вид, т.к. одно и то же значение любого критерия может быть получено путем бесконечного варьирования входящих величин. Уравнения могут быть записаны в виде:

- система обобщенных или критериальных уравнений

Критерии подобия могут быть двух видов: 1) состоящие из разноименных параметров; 2) имеющие периодический вид, т.к. представляют собой отношение одноименных параметров. Пример: для труб:

.

Относительные переменные также могут быть двух видов:

1) отношение переменной к одноименной величине, заданной по условию однозначности:

2) если по условию однозначности нельзя задать одноименную величину, то строится комплекс приводящий величину к безразмерному виду – число подобия:

В числа подобия входят определяемая величина. Критерий подобия состоит из заранее известных величин, заданных по условиям однозначности..

1) Критерий Рейнольдса  - определяет соотношение сил инерции и вязкости в однородном потоке. Это важнейший гидродинамический критерий для вынужденного движения. При движении потока в нем возникают возмущения, которые исходят от стенок канала или вносятся в поток извне. Влияние возмущений зависит от соотношения сил. Если преобладают силы вязкости возмущения гаснут и поток не меняет своей структуры. Если преобладают силы инерции возмущения развиваются дальше, поток меняет течение, изменяется его структура. Граница соотношения сил определяется по значению Reкр. Если Re<Reкр преобладают вязкие силы, Re>Reкр – силы инерции. Re характеризует движение при соизмеримости инерции и вязкости. Если в потоке преобладает какой-то один вид сил характер перестает зависеть от величины Re. В этом случае говорят, что течение автомодельно относительно критерия Re.

2) Критерий гидродинамической гомохронности  - определяет соотношение между периодом темпа внешних воздействий на поток и периодом перестройки скоростного поля. Используют только для нестационарных задач. - время, за которое проходит частица, движущаяся со скоростью V0, путь l0. Если в задаче время подлежит определению, то рассматривается не критерий, а число Струхала:

3) Критерий Фруда  - определяет соотношение между силами инерции и тяжести в потоке. Используется только в задачах, в которых гравитационные эффекты имеют важное значение. Однако в таких задачах часто сложно задать характерную скорость (при естественной конвекции), поэтому строится критерий, в котором исключается скорость:

 - критерий Галилея.

При гравитационном движении важное значение имеет параметрический критерий: .

Причем ρ и ρ0 – плотности не только в разных точках, но и в различных фазах.  - критерий Архимеда.

При гравитационном течении однофазной жидкости движение возникает в результате расширения:

 - коэффициент объемного расширения.

 - критерий Гросгофа.

4) Число Эйлера  - определяет соотношение сил давления и сил инерции; определяемая величина; т.к. часто давление в потоке неизвестно, то больший интерес представляет определение перепада давления на рассматриваемом участке .

 - безразмерный коэффициент сопротивления при очень низких скоростях, когда течение ламинарное , , в этих случаях рассматривают число Лагранжа, которое принимает постоянное значение:

22. Моделирование ГГД явлений

Одним из средств исследования потока является аэродинамический эксперимент. Достаточно сложно, дорого, а порой и невозможно выполнить эксперимент на действующем оборудовании. Для того, чтобы результаты полученные на моделях могли быть перенесены и использованы в действующих расчетах необходимо соблюдать условия подобия Кирпичева-Гухмана, т.е. течение в модели и образце должны иметь одинаковую физическую природу и описываться одними и теми же безразмерными уравнениями. Течения должны происходить в геометрически подобных каналах и должны быть подобраны все условия однозначности. Безразмерные критерии подобия должны иметь одинаковую величину. Рассмотрим условия моделирования вынужденного течения в цилиндрической трубе с прямой осью. Для соблюдения подобия необходимо, чтобы:

Свяжем одноименные величины с помощью констант подобия:

 - условие, определяющее выбор констант подобия

Например, если в модели и образце используется одинаковая жидкость с одинаковой температурой, то   . Это значит если размер модели в п раз меньше, чем размер образца, то для соблюдения подобия необходимо чтобы скорость в модели была в п раз больше. При моделировании часто возникает необходимость соблюдения подобия по нескольким критериям. В этом случае часто прибегают к приближенному моделированию, т.е. когда исследуется зависимость течения от одного критерия при условии, что от других критериев при этом же течение не зависит, т.е. автомодельно.

23. Ламинарное и турбулентное движение

При низких скоростях потока отмечается, что отдельные частицы или струйки жидкости движутся по плавным непересекающимся траекториям. Такое течение называется ламинарным, что означает слоистое. При увеличении скорости потока траектории отдельных струек приобретают волнообразный характер и через некоторое время струйка исчезает, перемешиваясь с жидкостью. Характер течения при этом изменился. Траектории отдельных частиц приобретают хаотичный неустановившийся характер. Такое течение называется турбулентным – хаотичным, вихревым. Рейнольдс установил, что смена режима происходит при значении . Причина перехода обусловлена влиянием возмущений, исходящих от стенок или вносимых в поток извне. Установлено, что если ликвидировать возмущение, т.е. отполировать тубу, сделать плавный вход потока в канал, то границу перехода можно значительно переместить в область более высоких . При  любые возмущения гаснут, следовательно  - нижняя граница значения области перехода. Смена режима происходит не сразу: сначала в потоке возникают отдельные очаги турбулентного движения, которые появляются и исчезают. Такое явление называют перемежаемостью:

 - общее время наблюдения за какой-то точкой

 - время существования режима в этой точке

При  - ламинарное

При  - турбулентное

 - переход

Переход ламинарного движения в турбулентное имеет очень большое практическое значение, т.к. определяет условия теплообмена, сопротивления потока, перемешивания жидкостей.

24. Пограничный слой и его характерные толщины

При обтекании любого тела потоком реальной жидкости поток как бы «прилипает» к поверхности. По мере удаления от поверхности скорость возрастает и, начиная с некоторого расстояния, скорость равна скорости набегающего или невозмущенного потока. В этом состоит проявление вязкости жидкости. Прандтль определил, что толщина слоя в котором проявляется вязкость увеличивается по мере продвижения потока. Чем меньше скорость набегающего потока, тем больше толщина слоя, в котором проявляется вязкость. Прандтль назвал эту часть жидкости у поверхности гидродинамическим пограничным слоем. Все течение он разбил на 3 части: 1 – гидродинамический пограничный слой – область, где сосредоточено влияние вязкости, 2 – след, 3 – невозмущенный поток. Во внешнем потоке вязкость можно не учитывать и считать жидкость идеальной, то есть без трения. Таким образом общая задача обтекания разбивается на 2 части: 1) течение жидкости в пограничном слое; 2) течение идеальной жидкости. Результаты решений должны совпадать на внешней границе пограничного слоя. Поскольку скорость в пограничном нарастает от 0 до скорости внешнего течения постепенно - асимптотически, поэтому δ определяется достаточно условно. Принято считать за δ такое значение у поперечной координаты, при котором скорость u отличается от U не более чем на 1-2%. u/U=0,98..0,99. Теория погранслоя использует и другие более точно определяемые толщины. Рассмотрим как влияет вязкость на кинематику (положение линий тока) и динамику (потерю количества движения).

Из-за торможения жидкости линия тока отклоняется от поверхности на расстояние δ. Расход жидкости между поверхностью и линией тока в плоском течении будет равен: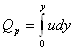

Если бы жидкость была идеальной, то та же линия тока располагалась бы ближе к поверхности на величину δ:

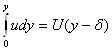
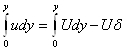
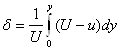
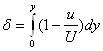
Максимальное значение δ будет равняться: δ= δmax= δ*

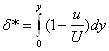 - толщина вытеснения.

Это более точно вычисляемая величина чем δ.

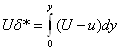
δ* может быть представлена, как линейный отрезок через который проходит секундный объемный расход идеальной жидкости, равный потере расхода через сечение погранслоя из-за торможения в реальном течении. Из-за торможения снижается и количество движения жидкости в погранслое. С количеством движения связана толщина потери импульса:

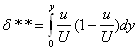
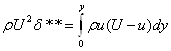
Толщина потери импульса может быть представлена как линейный отрезок, через который проходит количество движения жидкости равный потере количества движения через сечение в пограничном слое из-за торможения в реальном течении.

25. Переход ламинарного ПС в турбулентный

При обтекании поверхности потоком вязкой жидкости, начиная от критической точки образуется погранслой. Причем сначала слой является ламинарным, толщина его δ увеличивается, течение теряет устойчивость и происходит смена течения погранслоя. Смена происходит в некоторой области. Часто для упрощения считают, что переход происходит в точке.

Т.к. коэффициент сопротивления поверхности при ламинарном и турбулентном погранслое значительно отличаются по величине, меняются условия теплообмена. Определение границ перехода имеет большое практическое значение. Для определения границы перехода существуют теоретические и экспериментальные методы. В теоретических методах исследуется устойчивость течения ламинарного погранслоя и за границу перехода принимают точку потери устойчивости. Экспериментальные методы основаны на измерении распределений скорости или напряжения поверхностного трения. В точке перехода трение потока о стенку резко возрастает.

Если перемещать микротрубку вдоль обтекаемой поверхности на одинаковом расстоянии от нее, то по мере погружения микротрубки в ламинарный погранслой значение скорости, которое она будет показывать с увеличением х будет убывать. Вначале перехода ламинарного погранслоя в турбулентный (хкр1) профиль скорости начинает перестраиваться – становится более заполненным – прижимается к пластине, поэтому скорость возрастает. При x>хкр2 микротрубка погружается уже в турбулентный погранслой и поэтому скорость будет уменьшаться. За точку перехода принимают значение х, в которой скорость достигает минимума. Для определения границы перехода используют:

На положение хкр значительное влияние может оказать скорость изменения внешнего потока .

В конфузорной области, т.е. при разгоне внешнего потока переход затягивается, т.е. ламинарная зона увеличивается.

В диффузорной области ламинарный погранслой раньше теряет устойчивость, поэтому хкр уменьшается. Причины, вызывающие смену режима следующие:

-  возмущения, которые вносятся в погранслой из внешнего потока (внешний поток турбулизирован)

-  возмущения, исходящие от поверхности (шероховатости, стыки поверхностей)

Рассмотрим влияние турбулентности внешнего потока. Если степень турбулентности внешнего потока меньше 0,1%, то возмущение не влияет:

Если , то с увеличением ε хкр1 и хкр2 уменьшаются. Влияние шероховатости приводит к более ранней смене режимов.

Рассмотрим влияние величины U. Чем больше U, тем меньше хкр.

При турбулентном режиме течение у поверхности всегда существует область ламинарно текущей жидкости – вязкий подслой, толщина которого  от δ. Распределение скорости в вязком подслое линейное и описывается уравнением:

 (1)

В турбулентном ядре распределение скорости может быть описано универсальным логарифмическим профилем распределения:

 (2)

Между подслоем и ядром часто выделяют буферную область в которой физическая и критическая вязкость одного порядка. Поэтому уравнение (2) дает расхождение с экспериментальными данными в буферной области и на внешней границе пограничного слоя, где поток взаимодействует с нетурбулизированным потоком.

Т.к. при турбулентном погранслое коэффициент сопротивления значительно больше, то для снижения общего сопротивления хорошо обтекаемых тел (крыло, пластина, судно) необходимо затягивать переход, т.е. увеличивать протяженность ламинарного участка погранслоя. Для плохо обтекаемых тел (цилиндр, сфера) сопротивление определяется в первую очередь сопротивлением формы (давления). Сопротивление трения имеет малое значение. Сопротивление формы зависит от области отрыва потока. Чем больше область отрыва, тем больше сопротивление. При малых скоростях набегания (Re<Reкр) с поверхности цилиндра срывается ламинарный пограничный слой, который далее становится турбулентным (82°).

При Re>Reкр на цилиндре сначала образуется ламинарный погранслой, который преобразуется в турбулентный, который срывается при угле 140°.

Турбулентный погранслой лучше обменивается энергией с внешним потоком, чем ламинарный. Увеличение запаса энергии в турбулентном погранслое приводит к затягиванию точки отрыва до 140° и зона отрывного течения за цилиндром резко уменьшается, течение как бы приближается к идеальному, коэффициент сопротивления резко снижается. Это явление называется кризисом обтекания плохо обтекаемых тел.