
Рефераты по авиации и космонавтике
Рефераты по административному праву
Рефераты по безопасности жизнедеятельности
Рефераты по арбитражному процессу
Рефераты по архитектуре
Рефераты по астрономии
Рефераты по банковскому делу
Рефераты по сексологии
Рефераты по информатике программированию
Рефераты по биологии
Рефераты по экономике
Рефераты по москвоведению
Рефераты по экологии
Краткое содержание произведений
Рефераты по физкультуре и спорту
Топики по английскому языку
Рефераты по математике
Рефераты по музыке
Остальные рефераты
Рефераты по биржевому делу
Рефераты по ботанике и сельскому хозяйству
Рефераты по бухгалтерскому учету и аудиту
Рефераты по валютным отношениям
Рефераты по ветеринарии
Рефераты для военной кафедры
Рефераты по географии
Рефераты по геодезии
Рефераты по геологии
Рефераты по геополитике
Рефераты по государству и праву
Рефераты по гражданскому праву и процессу
Рефераты по кредитованию
Рефераты по естествознанию
Рефераты по истории техники
Рефераты по журналистике
Рефераты по зоологии
Рефераты по инвестициям
Рефераты по информатике
Исторические личности
Рефераты по кибернетике
Рефераты по коммуникации и связи
Рефераты по косметологии
Рефераты по криминалистике
Рефераты по криминологии
Рефераты по науке и технике
Рефераты по кулинарии
Рефераты по культурологии
Рефераты по авиации и космонавтике
Рефераты по административному праву
Рефераты по безопасности жизнедеятельности
Рефераты по арбитражному процессу
Рефераты по архитектуре
Рефераты по астрономии
Рефераты по банковскому делу
Рефераты по сексологии
Рефераты по информатике программированию
Рефераты по биологии
Рефераты по экономике
Рефераты по москвоведению
Рефераты по экологии
Краткое содержание произведений
Рефераты по физкультуре и спорту
Топики по английскому языку
Рефераты по математике
Рефераты по музыке
Остальные рефераты
Рефераты по биржевому делу
Рефераты по ботанике и сельскому хозяйству
Рефераты по бухгалтерскому учету и аудиту
Рефераты по валютным отношениям
Рефераты по ветеринарии
Рефераты для военной кафедры
Рефераты по географии
Рефераты по геодезии
Рефераты по геологии
Рефераты по геополитике
Рефераты по государству и праву
Рефераты по гражданскому праву и процессу
Рефераты по кредитованию
Рефераты по естествознанию
Рефераты по истории техники
Рефераты по журналистике
Рефераты по зоологии
Рефераты по инвестициям
Рефераты по информатике
Исторические личности
Рефераты по кибернетике
Рефераты по коммуникации и связи
Рефераты по косметологии
Рефераты по криминалистике
Рефераты по криминологии
Рефераты по науке и технике
Рефераты по кулинарии
Рефераты по культурологии
Контрольная работа: Математическое моделирование экономических ситуаций
Контрольная работа: Математическое моделирование экономических ситуаций
Тема 1
Задача 1
Имеется информация о количестве книг, полученных студентами по абонементу за прошедший учебный год.
| 2 | 4 | 4 | 7 | 6 | 5 | 2 | 2 | 3 | 4 |
| 4 | 3 | 6 | 5 | 4 | 7 | 6 | 6 | 5 | 3 |
| 2 | 4 | 2 | 3 | 5 | 7 | 4 | 3 | 3 | 2 |
| 4 | 5 | 6 | 6 | 10 | 4 | 3 | 3 | 2 | 3 |
Построить вариационный, ранжированный, дискретный ряд распределения, обозначив элементы ряда.
Решение:
Ранжированный вариационный ряд:
| 2 | 2 | 2 | 2 | 2 | 2 | 2 | 3 | 3 | 3 |
| 3 | 3 | 3 | 3 | 3 | 3 | 4 | 4 | 4 | 4 |
| 4 | 4 | 4 | 4 | 4 | 5 | 5 | 5 | 5 | 5 |
| 6 | 6 | 6 | 6 | 6 | 6 | 7 | 7 | 7 | 10 |
Дискретный вариационный ряд:
|
|
2 | 3 | 4 | 5 | 6 | 7 | 10 |
|
|
7 | 9 | 9 | 5 | 6 | 3 | 1 |
|
|
7/40 | 9/40 | 9/40 | 5/40 | 6/40 | 3/40 | 1/40 |
![]() – варианты,
– варианты, ![]() – частоты,
– частоты, ![]() =
=![]() /(7+9+9+5+6+3+1)=
/(7+9+9+5+6+3+1)=![]() /40
/40
Тема 2
Задача 1
В таблице приведены данные о продажах автомобилей в одном из автосалонов города за 1 квартал прошедшего года. Определите структуру продаж.
| Марка автомобиля | Число проданных автомобилей |
| Skoda | 245 |
| Hyundai | 100 |
| Daewoo | 125 |
| Nissan | 274 |
| Renault | 231 |
| Kia | 170 |
| Итого | 1145 |
Решение:
Показатель структуры (ОПС):
ОПС = Число проданных автомобилей / 1145
Skoda 245/1145=0.214
Hyundai 100/1145=0.087
Daewoo 125/1145=0.109
Nissan 274/1145=0.239
Renault 231/1145=0.203
Kia 170/1145=0.148
| Марка автомобиля | Число проданных автомобилей | Доля в продажах (%) |
| Skoda | 245 | 21.4 |
| Hyundai | 100 | 8.7 |
| Daewoo | 125 | 10.9 |
| Nissan | 274 | 23.9 |
| Renault | 231 | 20.3 |
| Kia | 170 | 14.8 |
| Итого | 1145 | 100 |
Тема 3
Задача 1
Имеется информация о численности студентов ВУЗов города и удельном весе (%) обучающихся студентов на коммерческой основе:
| ВУЗы города | Общее число студентов (тыс. чел.) | Из них удельный вес (%), обучающихся на коммерческой основе. |
| УГТУ—УПИ | 15 | 15 |
| УрГЭУ | 3 | 10 |
| УрГЮА | 7 | 20 |
Определить: 1) средний удельный вес студентов ВУЗов, обучающихся на коммерческой основе; 2) число этих студентов.
Решение:
1) Средний удельный вес студентов ВУЗов, обучающихся на коммерческой основе (%): (15+10+20)/3=15 %
Число студентов, обучающихся в этих трёх ВУЗах на коммерческой основе в сумме: 15*0.15+3*0.1+7*0.2=2.25+0.3+1.4=3.95 тыс. чел.
2) Число студентов ВУЗов, обучающихся на коммерческой основе в среднем: 3.95/3=1.317 тыс. чел.
Тема 4
Задача 1
При изучении влияния рекламы на размер среднемесячного вклада в банках района обследовано 2 банка. Получены следующие результаты:
| Размер месячного вклада, рубли | Число вкладчиков | |
| Банк с рекламой | Банк без рекламы | |
| До 500 | 3 | |
| 500-520 | 4 | |
| 520-540 | 17 | |
| 540-560 | 11 | 15 |
| 560-580 | 13 | 6 |
| 580-600 | 18 | 5 |
| 600-620 | 6 | |
| 620-640 | 2 | |
| Итого | 50 | 50 |
Определить:
1) для каждого банка: а) средний размер вклада за месяц; б) дисперсию вклада;
2) средний размер вклада за месяц для двух банков вместе.
3) Дисперсию вклада для 2-х банков, зависящую от рекламы;
4) Дисперсию вклада для 2-х банков, зависящую от всех факторов, кроме рекламы;
5) Общую дисперсию используя правило сложения;
6) Коэффициент детерминации;
7) Корреляционное отношение.
Решение:
(0+500)/2=250, (500+520)/2=510, (520+540)/2=530, (540+560)/2=550,
(560+580)/2=570, (580+600)/2=590, (600+620)/2=610, (620+640)/2=630.
| Размер месячного вклада, рубли | Средний размер месячного вклада, рубли | Число вкладчиков | |
| Банк с рекламой | Банк без рекламы | ||
| До 500 | 250 | 3 | |
| 500-520 | 510 | 4 | |
| 520-540 | 530 | 17 | |
| 540-560 | 550 | 11 | 15 |
| 560-580 | 570 | 13 | 6 |
| 580-600 | 590 | 18 | 5 |
| 600-620 | 610 | 6 | |
| 620-640 | 630 | 2 | |
| Итого | 50 | 50 | |
1) Для банка с рекламой средний размер вклада за месяц составил:
(550*11+570*13+590*18+610*6+630*2)/50=580 руб.
Для банка без рекламы средний размер вклада за месяц составил:
(250*3+510*4+530*17+550*15+570*6+590*5)/50=528,4 руб.
Для банка с рекламой дисперсия вклада будет:
![]() =((550-580)²*11+(570-580)²*13+(590-580)²*18+(610-580)²*6+
=((550-580)²*11+(570-580)²*13+(590-580)²*18+(610-580)²*6+
+(630-580)²*2)/50=(900*11+100*13+100*18+900*6+2500*2)/50=23400
/50=468
Для банка без рекламы дисперсия вклада будет:
![]() =((250-528,4)²*3+(510-528,4)²*4+(530-528,4)²*17+(550-528,4)²*15+
=((250-528,4)²*3+(510-528,4)²*4+(530-528,4)²*17+(550-528,4)²*15+
+(570-528,4)²*6+(590-528,4)²*5)/50=
= (232519,68+1354,24+43,52+6998,4+10383,36+18972,8)/50=
= 270272/50=5405,44
2) Средний размер вклада за месяц для двух банков вместе:
(250*3+510*4+530*17+550*(11+15)+570*(13+6)+590*(18+5)+610*6+63
0*2)/(50+50)=(750+2040+9010+14300+10830+13570+3660+1260)/100=55
4,2 руб. (или (580+528,4)/2=554,2 руб.)
3) Дисперсия вклада для 2-х банков, зависящая от рекламы:
![]() =((550-554,2)²*11+(570-554,2)²*13+(590-554,2)²*18+
=((550-554,2)²*11+(570-554,2)²*13+(590-554,2)²*18+
+(610-554,2)²*6+(630-554,2)²*2)/50=
=(17,64*11+249,64*13+1281,64*18+3113,64*6+5745,64*2)/50=
=56682/50=1133,64
4) Дисперсия вклада для 2-х банков, зависящая от всех факторов, кроме рекламы:
![]() =((250-554,2)²*3+(510-554,2)²*4+(530-554,2)²*17+(550-554,2)²*15+
=((250-554,2)²*3+(510-554,2)²*4+(530-554,2)²*17+(550-554,2)²*15+
+(570-554,2)²*6+(590-554,2)²*5)/50=
=(92537,64*3+1953,64*4+585,64*17+17,64*15+249,64*6+1281,64*5)/50
=303554/50=6071,08
5) Определить общую дисперсию используя правило сложения:
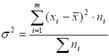
![]() =((250-554,2)²*3+(510-554,2)²*4+(530-554,2)²*17+(550-
=((250-554,2)²*3+(510-554,2)²*4+(530-554,2)²*17+(550-
554,2)²*(11+15)+
+(570-554,2)²*(13+6)+(590-554,2)²*(18+5)+(610-554,2)²*6+(630-
554,2)²*2)/
/100=(277612,92+7814,56+9955,88+458,64+4743,16+29477,72+18681,84+
+11491,28)/100=360236/100=3602,36
Тема 5
Задача 1
Имеется информация о выпуске продукции (работ, услуг), полученной на основе 10% выборочного наблюдения по предприятиям области:
| Группы предприятий по объему продукции, тыс. руб. | Число предприятий (f) |
|
До 100 100-200 200-300 300-400 400-500 500 и > |
28 52 164 108 36 12 |
| итого | 400 |
Определить:
1) по предприятиям, включенным в выборку:
а) средний размер произведенной продукции на одно предприятие;
б) дисперсию объема производства;
в) долю предприятий с объемом производства продукции более 400 тыс. руб.;
2) в целом по области с вероятностью 0,954 пределы, в которых можно ожидать:
а) средний объем производства продукции на одно предприятие;
б) долю предприятий с объемом производства продукции более 400 тыс. руб.;
3) общий объем выпуска продукции по области.
Решение:
| Группы предприятий по объему продукции, тыс. руб. | Средний объём продукции на группу, тыс. руб. | Число предприятий (f) |
|
До 100 100-200 200-300 300-400 400-500 500 и > |
50 150 250 350 450 550 |
28 52 164 108 36 12 |
| итого | 400 |
1) Средний размер произведенной продукции на одно предприятие:
(50*28+150*52+250*164+350*108+450*36+550*12)/400=110800/400=
=277 тыс. руб.
Дисперсия объема производства:
![]() =((50-277)²*28+(150-277)²*52+(250-277)²*164+(350-277)²*108+
=((50-277)²*28+(150-277)²*52+(250-277)²*164+(350-277)²*108+
+(450-277)²*36+(550-277)²*12)/400=4948400/400=12371
Доля предприятий с объемом производства продукции более 400 тыс. руб.:
(36+12)/400= 0,12 или 12%
2) Определить в целом по области с вероятностью 0,954 пределы, в которых можно ожидать:
а) средний объем производства продукции на одно предприятие:
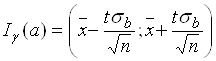
![]() 111,225
111,225
Величина t определяется по таблице значений функции Лапласа из равенства
![]() .
.
Следовательно, в нашем случае последнее равенство принимает вид
Ф(t)=0,954/2=0,477.
Из этого равенства по
таблице значений интегральной функции Лапласа ![]() находим значение t=2,00.
находим значение t=2,00.
√n=√400=20
Найдём нижний предел:
![]()
277-2*111,225/20=265,8775 тыс. руб.
Найдём верхний предел:
![]()
277+2*111,225/20=288,1225 тыс. руб.
Iγ(a)=( 265,8775 ; 288,1225)
б) долю предприятий с объемом производства продукции более 400 тыс. руб.:
Средняя: (450+550)/2=500 тыс. руб.
Найдём нижний предел:
![]()
500-2*111,225/20= 488,8775 тыс. руб.
Найдём верхний предел:
![]()
500+2*111,225/20= 511,1225 тыс. руб.
Iγ(a)=( 488,8775 ; 511,1225)
3) Общий объем выпуска продукции по области:
50*28+150*52+250*164+350*108+450*36+550*12=110800 тыс. руб.
Тема 6
Задача 1
Данные о площадях под картофелем до и после изменения границ района, тысяч гектаров:
|
периоды площадь под картофелем |
1 | 2 | 3 | 4 | 5 | 6 | 7 |
| До изменения границ района | 110 | 115 | 112 | ||||
| После изменения границ района | 208 | 221 | 229 | 234 | 230 |
Сомкнуть ряд, выразив площадь под картофелем в условиях изменения границ района.
Решение:
208/112=1,857 – коэффициент
110*1,857=204.27
115*1,857=213.55
115/112*100=102,68%
110/112*100=98,21%
221/208*100=106,25%
229/208*100=110,096%
234/208*100=112,5%
230/208*100=110,58%
|
периоды площадь под картофелем |
1 | 2 | 3 | 4 | 5 | 6 | 7 |
| До изменения границ района | 110 | 115 | 112 | ----- | ----- | ----- | ----- |
| После изменения границ района | ----- | ----- | 208 | 221 | 229 | 234 | 230 |
| Сомкнутый ряд | 204.27 | 213.55 | 208 | 221 | 229 | 234 | 230 |
| Сомкнутый ряд относительных величин в % к 3 периоду | 98,21 | 102,68 | 100,0 | 106,25 | 110,096 | 112,5 | 110,58 |
Тема 7
Задача 1
По нижеприведенным данным ответить на вопросы, поставленные в таблице, т.е. определить недостающие показатели
| Показатели | Изменение показателей в % к предыдущему кварталу «+»-увеличение, «-» - уменьшение | ||
| II квартал | III квартал | IV квартал | |
| Цена | ? | +10 | -2 |
| Натуральный объем продаж | Без изменения | ? | +5 |
| Товарооборот в денежном выражении | +8 | +5 | ? |
Решение:
Найдём в III квартале ip – так как 110-100=10% (+10) в этой ячейке, то значение индекса запишем 110/100=1,1 По аналогии заполним все ячейки.
| Индексы | Значения индексов | ||
| II квартал | III квартал | IV квартал | |
| ip | x | 1,1 | 0,98 |
| iq | 1,0 | y | 1,05 |
| Ipq | 1,08 | 1,05 | z |
Теперь найдём x,y,z:
Ipq= ip* iq
x= Ipq / iq=1,08/1=1,08 (+8)
y=1,05/1,1=0,95 (-5)
z=0,98*1,05=1,03 (+3)
Таблица примет вид:
| Показатели | Изменение показателей в % к предыдущему кварталу «+»-увеличение, «-» - уменьшение | ||
| II квартал | III квартал | IV квартал | |
| Цена | +8 | +10 | -2 |
| Натуральный объем продаж | 0 | -5 | +5 |
| Товарооборот в денежном выражении | +8 | +5 | +3 |
Тема 8
Задача 1
По пяти рабочим цеха имеются данные о квалификации и месячной выработке. Для изучения связи между квалификацией рабочих и их выработкой определить линейное уравнение связи и коэффициент корреляции. Дать интерпретацию коэффициентам регрессии и корреляции.
| Табельный номер рабочего | Разряд (y) | Выработка продукции за смену, шт. (x) |
|
1 2 3 4 5 |
6 2 3 5 4 |
130 60 70 110 90 |
Решение:
Линейное уравнение связи:
y=a+bx
6=a+130*b, a=6-130*b
5=a+110*b, a=5-110*b
6-130*b=5-110*b; 6-5=130*b-110*b; 1=20*b; b=1/20=0,05
6=a+0,05*130; a=6-0,05*130; a=-0,5
Линейное уравнение примет вид:
y=-0,5+0,05x
Проверка:
4=-0,5+0,05*90, 4=4; 3=-0,5+70/20, 3=3; 2=-0,5+60/20, 2=2,5 –
работник 2-го разряда перевыполняет норму и не вписывается в общую зависимость.
Коэффициент корреляции:
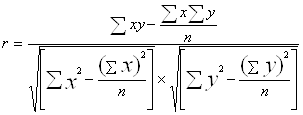
Найдём числитель (n=5):
(2*60+3*70+4*90+5*110+6*130)-(2+3+4+5+6)*
*(60+70+90+110+130)/5=2020-20*460/5=180
Σx²-(Σx)²/n=(60²+70²+90²+110²+130²)-(60+70+90+110+130)²/5=
=45600-211600/5=45600-42320=3280
Σy²-(Σy)²/n=(2²+3²+4²+5²+6²)-(2+3+4+5+6)²/5=90-400/5=90-80=10
r=180/√3280*√10=180/181,1077=0,99388
По шкале Чеддока связь классифицируется как функциональная. Поскольку (0,99388>0,99100), модель надёжна, связь статистически значима.
Тема 9
Задача 1
Имеются следующие данные за 2006 год:
· Численность населения, тыс. чел.: на 1 января - 430,0; на 1 апреля - 430,2; на 1 июля 430,3; на 1 октября - 430,7; на 1 января 2007 г. 430,8
· Число умерших, чел. - 8 170
· Число выбывших на постоянное жительство в другие населенные пункты, чел. - 570
· Коэффициент жизненности - 1,075
· Доля женщин в общей численности населения, % - 58
· Доля женщин в возрасте 15-49 лет в общей численности женщин, % -39
Определите: коэффициенты рождаемости, смертности, естественного, механического и общего прироста населения; число родившихся; число прибывших на постоянное жительство из других населенных пунктов; специальный коэффициент рождаемости.
Решение:
Коэффициент рождаемости
![]() :
:
N – кол-во родившихся, S – численность населения.
Средняя численность населения:
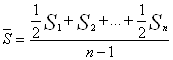 =
=
=(430/2+430,2+430,3+430,7+430,8/2)/(5-1)=
=1721,6/4=430,4
N=430,8-430,0=0,8 тыс. чел. (800 чел.) – За весь 2006 г.
n=1000*0,8/430,4=1,859 (чел./тыс. чел.)
Коэффициент смертности
![]() :
:
M – кол-во умерших.
m=1000*8,17/430,4=18,982 (чел./тыс. чел.) – за 2006 г.
Коэффициент естественного прироста населения
![]() :
:
Kn-m=1,859-18,982=-17,123 (чел./тыс. чел.)
Коэффициент механического прироста населения
![]() :
:
Коэффициент выбытия населения:
![]() =1000*0,57/430,4=1,324 (чел./тыс.
чел.)
=1000*0,57/430,4=1,324 (чел./тыс.
чел.)
Коэффициент прибытия населения:
![]() =0
=0
(В условиях задачи не указано сколько прибыло населения или чему равен Kпр, решение с двумя неизвестными невозможно. Будем считать его равным 0)
![]() =0-1,324=-1,324 (чел./тыс. чел.)
=0-1,324=-1,324 (чел./тыс. чел.)
Коэффициент общего прироста населения:
![]() =-17,123+(-1,324)=-18,447
=-17,123+(-1,324)=-18,447
Специальный коэффициент рождаемости:
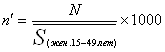 =1000*0,8/(430,4*0,39)= 4,766
=1000*0,8/(430,4*0,39)= 4,766
Тема 10
Задача 1
Имеются данные на конец года по РФ, млн. чел.:
- численность населения – 146,7
- экономически активное население – 66,7
- безработных, всего - 8,9, в том числе
зарегистрированных в службе занятости – 1,93.
Определить: 1) уровень экономически активного населения; 2) уровень занятости; 3) уровень безработицы; 4) уровень зарегистрированных безработных; 5) коэффициент нагрузки на 1 занятого в экономике.
Решение:
Коэффициент экономически активного населения:
![]() =66,7/146,7=0,45467=45,467%
=66,7/146,7=0,45467=45,467%
Коэффициент занятости
![]() :
:
занятые = экономически активные - безработные =66,7-8,9=57,8 млн. чел.
![]() =57,8/66,7=0,8666=86,66%
=57,8/66,7=0,8666=86,66%
Коэффициент безработицы:
![]() =8,9/66,7=0,1334=13,34%
=8,9/66,7=0,1334=13,34%
Уровень зарегистрированных безработных:
зарегистрированные в службе занятости / экономически активные=1,93/66,7 = 0,0289=2,89%
Коэффициент нагрузки на одного занятого в экономике – это число незанятых в экономике, приходящееся на одного занятого:
S - численность населения.
![]() = (146,7-57,8)/57,8=1,538
= (146,7-57,8)/57,8=1,538