
Рефераты по авиации и космонавтике
Рефераты по административному праву
Рефераты по безопасности жизнедеятельности
Рефераты по арбитражному процессу
Рефераты по архитектуре
Рефераты по астрономии
Рефераты по банковскому делу
Рефераты по сексологии
Рефераты по информатике программированию
Рефераты по биологии
Рефераты по экономике
Рефераты по москвоведению
Рефераты по экологии
Краткое содержание произведений
Рефераты по физкультуре и спорту
Топики по английскому языку
Рефераты по математике
Рефераты по музыке
Остальные рефераты
Рефераты по биржевому делу
Рефераты по ботанике и сельскому хозяйству
Рефераты по бухгалтерскому учету и аудиту
Рефераты по валютным отношениям
Рефераты по ветеринарии
Рефераты для военной кафедры
Рефераты по географии
Рефераты по геодезии
Рефераты по геологии
Рефераты по геополитике
Рефераты по государству и праву
Рефераты по гражданскому праву и процессу
Рефераты по кредитованию
Рефераты по естествознанию
Рефераты по истории техники
Рефераты по журналистике
Рефераты по зоологии
Рефераты по инвестициям
Рефераты по информатике
Исторические личности
Рефераты по кибернетике
Рефераты по коммуникации и связи
Рефераты по косметологии
Рефераты по криминалистике
Рефераты по криминологии
Рефераты по науке и технике
Рефераты по кулинарии
Рефераты по культурологии
Рефераты по авиации и космонавтике
Рефераты по административному праву
Рефераты по безопасности жизнедеятельности
Рефераты по арбитражному процессу
Рефераты по архитектуре
Рефераты по астрономии
Рефераты по банковскому делу
Рефераты по сексологии
Рефераты по информатике программированию
Рефераты по биологии
Рефераты по экономике
Рефераты по москвоведению
Рефераты по экологии
Краткое содержание произведений
Рефераты по физкультуре и спорту
Топики по английскому языку
Рефераты по математике
Рефераты по музыке
Остальные рефераты
Рефераты по биржевому делу
Рефераты по ботанике и сельскому хозяйству
Рефераты по бухгалтерскому учету и аудиту
Рефераты по валютным отношениям
Рефераты по ветеринарии
Рефераты для военной кафедры
Рефераты по географии
Рефераты по геодезии
Рефераты по геологии
Рефераты по геополитике
Рефераты по государству и праву
Рефераты по гражданскому праву и процессу
Рефераты по кредитованию
Рефераты по естествознанию
Рефераты по истории техники
Рефераты по журналистике
Рефераты по зоологии
Рефераты по инвестициям
Рефераты по информатике
Исторические личности
Рефераты по кибернетике
Рефераты по коммуникации и связи
Рефераты по косметологии
Рефераты по криминалистике
Рефераты по криминологии
Рефераты по науке и технике
Рефераты по кулинарии
Рефераты по культурологии
Реферат: Новые реалии в физическом содержании великих уравнений электродинамики Максвелла
Реферат: Новые реалии в физическом содержании великих уравнений электродинамики Максвелла
НОВЫЕ РЕАЛИИ В ФИЗИЧЕСКОМ СОДЕРЖАНИИ
ВЕЛИКИХ УРАВНЕНИЙ ЭЛЕКТРОДИНАМИКИ МАКСВЕЛЛА
Сидоренков В.В.
МГТУ им. Н.Э. Баумана
На основе анализа традиционных электродинамических уравнений Максвелла выявлены принципиально новые реалии в их физическом содержании, иллюстрирующие подлинное величие и грандиозные скрытые возможности этих уравнений в отношении полноты охвата явлений электромагнетизма, в итоге тем самым удалось провести модернизацию концептуальных представлений классической электродинамики о структуре и свойствах электромагнитного поля, которое является лишь только одной из равноправных составляющих векторного четырехкомпонентного единого электродинамического поля.
Общепринято считать, что все известные явления
электромагнетизма обусловлены существованием и взаимодействием с материальными
средами электромагнитного поля, с двумя векторными компонентами
электрической ![]() магнитной
магнитной ![]() напряженности. Свойства этого поля физически полно и математически
исчерпывающе описываются системой взаимосвязанных электродинамических уравнений,
первоначальная форма и структура которых была сформулирована Максвеллом [1]. Максвелл
прожил короткую (48 лет) жизнь, и свои гениальные уравнения он так и не успел
привести в единую логически систему. К сожалению, при жизни его теория электромагнитного
поля не нашла должного признания в научной среде, более того у некоторых коллег
отношение к ней было почти враждебным, вплоть до полного неприятия: она считалась
непонятной, математически нестрогой и логически необоснованной.
напряженности. Свойства этого поля физически полно и математически
исчерпывающе описываются системой взаимосвязанных электродинамических уравнений,
первоначальная форма и структура которых была сформулирована Максвеллом [1]. Максвелл
прожил короткую (48 лет) жизнь, и свои гениальные уравнения он так и не успел
привести в единую логически систему. К сожалению, при жизни его теория электромагнитного
поля не нашла должного признания в научной среде, более того у некоторых коллег
отношение к ней было почти враждебным, вплоть до полного неприятия: она считалась
непонятной, математически нестрогой и логически необоснованной.
Впоследствии, после триумфа теории Максвелла - открытия электромагнитных волн (Герц, 1888г), система этих уравнений была модернизирована Герцем и Хевисайдом, где по существу новации заключались лишь в уменьшения числа (с 8 до 4) исходных уравнений системы. Однако если говорить о положительном эффекте такой модификации, то он заключался в том, что в новом варианте уравнения были для того времени концептуально логически обозримы и физически более последовательны, имели удобный математически векторный вид и в определенной мере законченную форму. В современном окончательном виде именно эту модифицированную систему уравнений [2]:
(a) ![]() ,
(b)
,
(b) ![]() ,
,
(c) 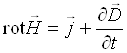 , (d)
, (d) ![]() ,
(1)
,
(1)
и стали
называть уравнениями Максвелла классической электродинамики. Здесь векторы
напряженности электрического ![]() и магнитного
и магнитного ![]() полей связаны посредством материальных соотношений:
полей связаны посредством материальных соотношений:
![]() ,
, ![]() ,
, ![]() , (2)
, (2)
с векторами электрической ![]() и
магнитной
и
магнитной ![]() индукций, вектором
плотности электрического тока
индукций, вектором
плотности электрического тока ![]() ,
которые представляют собой отклик среды на наличие в ней электромагнитного поля.
Соответственно,
,
которые представляют собой отклик среды на наличие в ней электромагнитного поля.
Соответственно, ![]() - объемная
плотность стороннего заряда,
- объемная
плотность стороннего заряда, ![]() и
и
![]() - электрическая и
магнитная постоянные,
- электрическая и
магнитная постоянные, ![]() - удельная электрическая проводимость, относительные
диэлектрическая
- удельная электрическая проводимость, относительные
диэлектрическая ![]() и магнитная
и магнитная ![]() проницаемости среды.
проницаемости среды.
Принципиальная особенность этих динамических релятивистски инвариантных
уравнений (1) состоит в том, что в их структуре заложена отражающая обобщение
опытных данных основная аксиома классической электродинамики - неразрывное
единство переменных во времени электрической и магнитной компонент такого
поля, которое и называют электромагнитным полей. Прямым фундаментальным
следствием уравнений Максвелла является вывод о том, что описываемое ими
электромагнитное поле распространяется в свободном пространстве посредством поперечных
волн, скорость которых определяется лишь электрическими и магнитными
параметрами среды, заполняющей это пространство (например, в отсутствие
поглощения ![]() ). Совместное решение
уравнений системы (1) позволяет также ответить на вопрос, что переносят эти
волны и получить аналитическую формулировку закона сохранения электромагнитной
энергии:
). Совместное решение
уравнений системы (1) позволяет также ответить на вопрос, что переносят эти
волны и получить аналитическую формулировку закона сохранения электромагнитной
энергии:
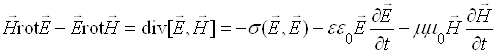 , (3)
, (3)
согласно которому поток электромагнитной энергии ![]() компенсирует в данной точке
среды джоулевы (тепловые) потери за счет электропроводности (первое слагаемое в
правой части) и изменяет электрическую и магнитную энергии, либо наоборот:
процессы, описываемые правой частью соотношения (3), порождают поток
компенсирует в данной точке
среды джоулевы (тепловые) потери за счет электропроводности (первое слагаемое в
правой части) и изменяет электрическую и магнитную энергии, либо наоборот:
процессы, описываемые правой частью соотношения (3), порождают поток ![]() . При этом характеризующий
энергетику данного явления вектор Пойнтинга плотности потока электромагнитной
энергии
. При этом характеризующий
энергетику данного явления вектор Пойнтинга плотности потока электромагнитной
энергии ![]() , связанный с вектором объемной
плотности электромагнитного импульса
, связанный с вектором объемной
плотности электромагнитного импульса ![]() ,
отличен от нуля только там, где одновременно присутствуют электрическая и магнитная
компоненты поля, векторы
,
отличен от нуля только там, где одновременно присутствуют электрическая и магнитная
компоненты поля, векторы ![]() и
и ![]() которых неколлинеарны.
которых неколлинеарны.
Однако следует указать и на весьма ограниченный диапазон явных возможностей уравнений (1), поскольку в их рамках в принципе нельзя представить раздельное существование чисто электрических либо магнитных волн, переносящих электродинамические потоки только электрической или только магнитной энергии, хотя процессы соответствующей поляризации сред наблюдаются в эксперименте, существуют раздельно и энергетически друг от друга независимы. Кроме того, далеко не ясен вопрос о физической реализации момента импульса электромагнитного поля, соответственно, переносящих его волн, и как это явление соотносится с уравнениями Максвелла. Заметим, что еще со времен Пойнтинга его безуспешно пытаются описать этими уравнениями (см., например, результаты анализа в статье [3]).
В этой связи попытаемся аргументированно прояснить сложившуюся ситуацию, для чего продолжим далее модернизацию теперь уже уравнений (1), где нашей основной задачей будет выявление концептуально новых реалий в физическом содержании уравнений Максвелла, иллюстрирующих величие и грандиозные скрытые возможности этих уравнений в отношении полноты охвата наблюдаемых в Природе явлений электромагнетизма.
Поскольку «все новое – это хорошо забытое старое», то обратимся к физическим представлениям о векторном потенциале электромагнитного поля, который, по словам Максвелла [1], “может быть признан фундаментальной величиной в теории электромагнетизма”. Однако в наше время векторные потенциалы как физическую реальность по существу не рассматривают, им отводят лишь роль вспомогательной математической функции, в ряде случаев упрощающей вычисления. Такой общепринятый сегодня взгляд на векторные потенциалы берет начало от Герца и Хевисайда, о чем прямо говорится в цитате из статьи Герца (перевод в [4]): “… мне не кажется, что какая либо выгода достигается при введении векторного потенциала в фундаментальные уравнения; более того, хотелось бы видеть в этих уравнениях связь между физическими величинами, которые можно наблюдать, а не между величинами, которые служат лишь для вычислений ”. Не доводя до абсурдной абсолютизации мнение классика, в целом с этим приходится согласиться, так как такой взгляд обусловлен взаимно неоднозначной связью полей и их потенциалов, не допускающей прямых измерений последних, но, что еще более важно, использование векторных потенциалов строго в рамках уравнений Максвелла не приводит в явном виде к дополнительным, не известным прежде следствиям.
Удивительно, но это табу на развитие физических
представлений в классической электродинамике существует со времен Герца, и его
продолжают настоятельно культивировать уже более века. Другое подобное табу -
это завидное упорство в применении инородной электродинамике гауссовой системы
единиц, где по существу игнорируется физическое содержание электродинамических
соотношений и выдвигается на передний план формализм математики, что создает
путаница физических понятий и мешает действительно разобраться в них.
Конкретный пример такого «математического шабаша» в электромагнетизме можно
встретить даже в учебниках, когда без разбора пишут, кстати, не считаясь с
мнением Максвелла ([1] п. 12, 14), как «![]() »
так и «
»
так и «![]() » либо «
» либо «![]() » и «
» и «![]() ». Вызывает недоумение неприятие
до сей поры и логически необъяснимый корпоративный снобизм многих
профессиональных физиков в отношении к широко используемой в технических
дисциплинах международной системы единиц СИ. По нашему мнению, налицо полный
концептуальный застой и даже стагнация в теории электромагнетизма. При этом,
несмотря на все вышесказанное, опять же в учебной литературе повсеместно с
помпой утверждается, что именно данная область физического знания наиболее
полно разработана во всех ее аспектах и является вершиной человеческого гения.
». Вызывает недоумение неприятие
до сей поры и логически необъяснимый корпоративный снобизм многих
профессиональных физиков в отношении к широко используемой в технических
дисциплинах международной системы единиц СИ. По нашему мнению, налицо полный
концептуальный застой и даже стагнация в теории электромагнетизма. При этом,
несмотря на все вышесказанное, опять же в учебной литературе повсеместно с
помпой утверждается, что именно данная область физического знания наиболее
полно разработана во всех ее аспектах и является вершиной человеческого гения.
Однако к настоящему времени исследованиями в области электродинамики, квантовой механики, сверхпроводимости достоверно установлено, что в фундаментальных уравнениях должны фигурировать не электромагнитные поля, а именно их потенциалы. В частности, эффекты Ааронова-Бома, Джозефсона, Мейснера реализуются в поле магнитной компоненты векторного потенциала [4], проявляющего себя тем самым вполне наблюдаемой физической величиной. Известно предложение о применении указанного поля векторного потенциала в технологиях обработки разного рода материалов [5]. Отметим также сообщение [6], где на основе формального использования представлений об электромагнитном векторном потенциале металлического проводника с током установлено, что в проводник при электропроводности вместе с потоком электромагнитной энергии (вектора Пойнтинга) поступают потоки чисто электрической и чисто магнитной энергии, момента электромагнитного импульса. Таким образом, имеем серьезную, необходимо требующую разрешения проблему, в которой надо должным образом проанализировать известные либо вскрыть новые реалии в физическом содержании уравнений Максвелла, в частности, понять роль и место векторных потенциалов в явлениях электромагнетизма. Покажем, как это можно сделать!
Поставленная
задача и проведенный в этом направлении анализ показал, что исходные
соотношения первичной взаимосвязи электромагнитного поля с компонентами ![]() и
и ![]() напряженностей и поля электромагнитного
векторного потенциала с электрической
напряженностей и поля электромагнитного
векторного потенциала с электрической ![]() и
магнитной
и
магнитной ![]() компонентами можно
действительно получить при использовании непосредственно системы максвелловских
уравнений (1):
компонентами можно
действительно получить при использовании непосредственно системы максвелловских
уравнений (1):
(a) ![]() , (b)
, (b)
![]() ,
,
(c) 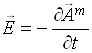 , (d)
, (d)  .
(4)
.
(4)
Здесь соотношение (4a) для магнитной компоненты векторного потенциала ![]() вводится с помощью
уравнения (1d), так как дивергенция ротора произвольного векторного поля
тождественно равна нулю. Аналогично соотношение (4b) для электрической компоненты
векторного потенциала
вводится с помощью
уравнения (1d), так как дивергенция ротора произвольного векторного поля
тождественно равна нулю. Аналогично соотношение (4b) для электрической компоненты
векторного потенциала ![]() следует из
уравнения (1b) при
следует из
уравнения (1b) при ![]() , справедливого
для сред с локальной электронейтральностью. Однозначность
функций векторного потенциала, то есть чисто вихревой характер таких полей,
обеспечивается условием кулоновской калибровки: div
, справедливого
для сред с локальной электронейтральностью. Однозначность
функций векторного потенциала, то есть чисто вихревой характер таких полей,
обеспечивается условием кулоновской калибровки: div![]() .
Далее подстановка соотношения (4a) для
.
Далее подстановка соотношения (4a) для ![]() в уравнение вихря
электрической напряженности (1a) приводит к известной
формуле (4с) связи полей векторов
в уравнение вихря
электрической напряженности (1a) приводит к известной
формуле (4с) связи полей векторов ![]() и
и ![]() [2], описывающей закон электромагнитной
индукции Фарадея. Поскольку мы рассматриваем только вихревые поля, то формально
следующий из таких рассуждений электрический скалярный потенциал
[2], описывающей закон электромагнитной
индукции Фарадея. Поскольку мы рассматриваем только вихревые поля, то формально
следующий из таких рассуждений электрический скалярный потенциал ![]() здесь не рассматривается. Аналогичная
подстановка соотношения (4b) для
здесь не рассматривается. Аналогичная
подстановка соотношения (4b) для ![]() в уравнение вихря
магнитной напряженности (1c) с учетом соотношений (2) дает
формулу (4d) связи полей векторов
в уравнение вихря
магнитной напряженности (1c) с учетом соотношений (2) дает
формулу (4d) связи полей векторов ![]() и
и ![]() , где
, где ![]() - постоянная
времени релаксации электрического заряда в среде за счет ее электропроводности.
- постоянная
времени релаксации электрического заряда в среде за счет ее электропроводности.
Как видим, полученные
соотношения являются основой для интерпретации физического смысла поля электромагнитного
векторного потенциала (см. работу [7]), выяснения его роли и места в явлениях
электромагнетизма. Однако самое главное и конструктивно перспективное в них то,
что они представляют собой логически связанную систему дифференциальных уравнений,
описывающих свойства необычного вихревого векторного поля, состоящего их
четырех полевых векторных компонент ![]() ,
,
![]() ,
, ![]() и
и
![]() , которое
условно назовем единое электродинамическое поле.
, которое
условно назовем единое электродинамическое поле.
Объективность
существования указанного единого поля однозначно и убедительно
иллюстрируется основным фундаментальным следствием из соотношений (4), которое
состоит в том, что подстановки (4c) в (4b) и (4d) в (4a)
приводят к системе новых электродинамических уравнений для поля
электромагнитного векторного потенциала с электрической ![]() и магнитной
и магнитной ![]() компонентами. Видно, что математически
структура этих уравнений, полностью аналогична системе традиционных уравнений электродинамики
Максвелла (1):
компонентами. Видно, что математически
структура этих уравнений, полностью аналогична системе традиционных уравнений электродинамики
Максвелла (1):
(a) rot![]() , (b)
div
, (b)
div![]() ,
,
(c) rot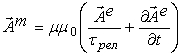 , (d) div
, (d) div![]() .
(5)
.
(5)
Чисто
вихревой характер компонент ![]() и
и
![]() поля
векторного потенциала обеспечивается условием калибровки посредством
дивергентных уравнений (5b) и (5d),
которые также представляют собой для уравнений (5a) и (5c) начальные условия в математической задаче Коши, что делает
систему (5) замкнутой. Неординарность уравнений системы (5) вполне очевидна, поскольку
в каждом одном роторном уравнении компоненты потенциала
поля
векторного потенциала обеспечивается условием калибровки посредством
дивергентных уравнений (5b) и (5d),
которые также представляют собой для уравнений (5a) и (5c) начальные условия в математической задаче Коши, что делает
систему (5) замкнутой. Неординарность уравнений системы (5) вполне очевидна, поскольку
в каждом одном роторном уравнении компоненты потенциала ![]() или
или ![]() содержится информация о
свойствах обоих роторных уравнений электромагнитных полей
содержится информация о
свойствах обоих роторных уравнений электромагнитных полей ![]() и
и ![]() системы (1). Убедиться в
этом посредством дифференцирования по времени и пространству этих уравнений с
учетом соотношений (4) предоставим читателю. Дивергентные уравнения системы (5)
с помощью дифференцирования их по времени преобразуются в соответствующие
уравнения системы (1) при
системы (1). Убедиться в
этом посредством дифференцирования по времени и пространству этих уравнений с
учетом соотношений (4) предоставим читателю. Дивергентные уравнения системы (5)
с помощью дифференцирования их по времени преобразуются в соответствующие
уравнения системы (1) при ![]() .
.
Однако
вернемся к соотношениям (4) единого электродинамического поля. Подстановки
соотношения (4с) в продифференцированное по времени соотношение (4a) и аналогично (4d) в (4b) дают систему электродинамических уравнений электромагнитного
поля (1) при ![]() , где
уравнения (1d) и (1b)
получаются взятием дивергенции от (4a) и (4b). Уравнения (1а) и (1с) можно также получить, если взять
ротор от (4с) и (4d) при подстановке в них (4а) и (4b).
, где
уравнения (1d) и (1b)
получаются взятием дивергенции от (4a) и (4b). Уравнения (1а) и (1с) можно также получить, если взять
ротор от (4с) и (4d) при подстановке в них (4а) и (4b).
Применение
операции ротора к (4c) и подстановка в него (4a) с учетом (4d) преобразует систему
(4) в еще одну систему теперь уже уравнений электрического поля с компонентами
напряженности ![]() и векторного
потенциала
и векторного
потенциала ![]() :
:
(a) rot , (b) div
, (b) div![]() ,
,
(c) rot![]() ,
(d) div
,
(d) div![]() . (6)
. (6)
Соответственно
взятие ротора от соотношения (4d) и подстановка в него
(4b) с учетом (4c) снова
преобразует систему соотношений (4) в еще одну новую систему уравнений
классической электродинамики систему уравнений магнитного поля с
компонентами напряженности ![]() и
векторного потенциала
и
векторного потенциала ![]() :
:
(a) rot , (b) div
, (b) div![]() ,
,
(c) rot![]() ,
(d) div
,
(d) div![]() .
(7)
.
(7)
Сделаем общее математическое замечание о дивергентных уравнениях во всех
системах. Как уже говорилось, уравнения div![]() являются
калибровкой, обеспечивающей однозначность функции векторного потенциала
являются
калибровкой, обеспечивающей однозначность функции векторного потенциала ![]() , поэтому, согласно
симметрии уравнений в рассматриваемых системах, другие дивергентные уравнения:
(1b) при
, поэтому, согласно
симметрии уравнений в рассматриваемых системах, другие дивергентные уравнения:
(1b) при ![]() , (1d), (6b) и (7b)
с математической точки зрения также следует считать соответствующими калибровками
для функций вихревых полей
, (1d), (6b) и (7b)
с математической точки зрения также следует считать соответствующими калибровками
для функций вихревых полей ![]() и
и
![]() .
.
Проведем анализ полученных выше систем уравнений [8], специфика которых состоит
в том, что, являясь модификацией уравнений Максвелла электромагнитных полей,
они справедливы теперь в таких областях пространства, где присутствуют
одновременно поля и их векторные потенциалы, либо только потенциалы. Согласно
структуре представленных уравнений, описываемые ими поля распространяются в
пространстве в виде волн, скорость которых определяется электрическими и
магнитными параметрами среды, заполняющей это пространство: ![]() ,
, ![]() и
и ![]() . В этом можно убедиться,
взяв, как обычно, ротор от одного из роторных уравнений системы, и после
чего подставить в него другое роторное уравнение той же системы. В качестве
иллюстрации получим, например, для системы (6) волновое уравнение относительно
. В этом можно убедиться,
взяв, как обычно, ротор от одного из роторных уравнений системы, и после
чего подставить в него другое роторное уравнение той же системы. В качестве
иллюстрации получим, например, для системы (6) волновое уравнение относительно ![]() :
:
rot rot![]() grad div
grad div![]() rot
rot![]()
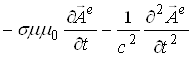 ,
,
где, согласно (6b), div![]() , а Δ
– оператор Лапласа. Таким образом, имеем теперь волновые уравнения не только
для электромагнитных полей
, а Δ
– оператор Лапласа. Таким образом, имеем теперь волновые уравнения не только
для электромагнитных полей ![]() и
и ![]() , но и для их векторных
потенциалов
, но и для их векторных
потенциалов ![]() и
и ![]() в парных комбинациях этих
четырех уравнений в зависимости от системы. В итоге возникает физически
очевидный, принципиальный вопрос: какие это волны, и что они переносят? Результаты
подробного изучения особенностей распространения составляющих единого
электродинамического поля в виде плоских волн в материальных средах
изложено в публикации [9]. В настоящей работе для нас представляет наибольший
интерес прояснить физическое содержание рассматриваемых здесь систем
электродинамических уравнений.
в парных комбинациях этих
четырех уравнений в зависимости от системы. В итоге возникает физически
очевидный, принципиальный вопрос: какие это волны, и что они переносят? Результаты
подробного изучения особенностей распространения составляющих единого
электродинамического поля в виде плоских волн в материальных средах
изложено в публикации [9]. В настоящей работе для нас представляет наибольший
интерес прояснить физическое содержание рассматриваемых здесь систем
электродинамических уравнений.
Подобно
вектору Пойнтинга ![]() плотности
потока электромагнитной энергии полей системы уравнений (1) рассмотрим другой
потоковый вектор
плотности
потока электромагнитной энергии полей системы уравнений (1) рассмотрим другой
потоковый вектор ![]() ,
который, судя по размерности, описывает электрическую энергию, приходящуюся на
единицу площади поверхности. Для аргументированного обоснования возможности
существования такого вектора и установления его статуса воспользуемся
уравнениями системы (6) и с помощью стандартных вычислений (см. (3)) получим
,
который, судя по размерности, описывает электрическую энергию, приходящуюся на
единицу площади поверхности. Для аргументированного обоснования возможности
существования такого вектора и установления его статуса воспользуемся
уравнениями системы (6) и с помощью стандартных вычислений (см. (3)) получим
![]()
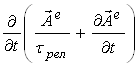 (8)
(8)
- соотношение, описывающее энергетику реализации процесса электрической поляризации среды в данной точке. Как видим, уравнения электрического поля системы (6) описывают чисто электрические явления, в том числе, поперечные электрические волны, переносящие поток электрической энергии.
Аналогичным
образом можно ввести еще один потоковый вектор ![]() , размерность которого
соответствует поверхностной плотности магнитной энергии в соотношении,
описывающем энергетику процесса намагничивания среды в данной
точке:
, размерность которого
соответствует поверхностной плотности магнитной энергии в соотношении,
описывающем энергетику процесса намагничивания среды в данной
точке:
![]()
 . (9)
. (9)
Итак, уравнения магнитного поля системы (7) рассматривают чисто магнитные явления, устанавливают реальность поперечных магнитных волн, переносящих поток магнитной энергии.
Полученные
соотношения баланса (8) и (9) описывают энергетику условий реализации обычной
электрической или магнитной поляризации среды (первое слагаемое правой части
соотношений) посредством переноса извне в данную точку потоком вектора ![]() или
или ![]() соответствующей энергии. Однако
эти соотношения устанавливают также наличие эффектов динамической поляризации
вещества (в частности, проводящих сред) за счет действия переменных во времени
электрической или магнитной компонент поля электромагнитного векторного
потенциала. Надо сказать, что явления динамической поляризации уже имеют прямое
экспериментальное воплощение: это эффекты электродинамической индукции в
металлах [10] и динамического намагничивания в ферритах и магнитоупорядоченных
металлах [11].
соответствующей энергии. Однако
эти соотношения устанавливают также наличие эффектов динамической поляризации
вещества (в частности, проводящих сред) за счет действия переменных во времени
электрической или магнитной компонент поля электромагнитного векторного
потенциала. Надо сказать, что явления динамической поляризации уже имеют прямое
экспериментальное воплощение: это эффекты электродинамической индукции в
металлах [10] и динамического намагничивания в ферритах и магнитоупорядоченных
металлах [11].
Подобно
соотношениям (8) и (9) из уравнений системы (5) следует соотношение баланса
передачи в данную точку момента импульса, реализуемого компонентами поля электромагнитного
векторного потенциала посредством потокового вектора ![]() :
:
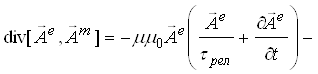
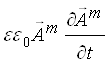 . (10)
. (10)
Здесь момент электромагнитного импульса в проводящей среде создается электрической компонентой векторного потенциала, стационарной в том числе, а в среде диэлектрика – переменными во времени электрической и магнитной компонентами.
Как видим,
именно уравнения поля электромагнитного векторного потенциала (5)
описывают волны, переносящие в пространстве поток момента импульса, которые со
времен Пойнтинга безуспешно пытаются описать с помощью уравнений электромагнитного
поля (1) (см. анализ в [3]). Существенно, что сами по себе волны векторного
потенциала принципиально не способны переносить энергию, поскольку в уравнениях
(4) поля ![]() и
и ![]() отсутствуют. В этой связи
укажем на пионерские работы [12], где обсуждается неэнергетическое
(информационное) взаимодействие векторного потенциала со средой при передаче в
ней потенциальных волн и их детектирование с помощью эффекта, аналогичного
эффекту Ааронова-Бома. Однако, как иллюстрирует система соотношений (4) и показано
в работе [9], распространение волн электромагнитного векторного потенциала в
принципе невозможно без присутствия их сопровождающих волн электромагнитного поля,
соответственно, наоборот.
отсутствуют. В этой связи
укажем на пионерские работы [12], где обсуждается неэнергетическое
(информационное) взаимодействие векторного потенциала со средой при передаче в
ней потенциальных волн и их детектирование с помощью эффекта, аналогичного
эффекту Ааронова-Бома. Однако, как иллюстрирует система соотношений (4) и показано
в работе [9], распространение волн электромагнитного векторного потенциала в
принципе невозможно без присутствия их сопровождающих волн электромагнитного поля,
соответственно, наоборот.
Таким
образом, соотношения (4) действительно следует считать системой уравнений
вихревого векторного четырехкомпонентного единого электродинамического поля,
базирующегося на исходной своей составляющей - поле электромагнитного
векторного потенциала, состоящего из двух взаимно ортогональных электрической ![]() и
магнитной
и
магнитной ![]() векторных полевых компонент. При этом поле векторного
потенциала своим существованием реализует функционально связанные с ним другие
составляющие единого поля: электромагнитное поле с векторными
компонентами
векторных полевых компонент. При этом поле векторного
потенциала своим существованием реализует функционально связанные с ним другие
составляющие единого поля: электромагнитное поле с векторными
компонентами ![]() и
и ![]() , электрическое поле
с компонентами
, электрическое поле
с компонентами ![]() и
и ![]() , магнитное поле
с компонентами
, магнитное поле
с компонентами ![]() и
и ![]() . Отмеченная здесь
структура и взаимосвязь составляющих единого электродинамического поля
сохраняется и в статической асимптотике. Логика построения систем полевых
уравнений для стационарных составляющих единого поля и анализ физического
содержания таких уравнений изложены в работе [13].
. Отмеченная здесь
структура и взаимосвязь составляющих единого электродинамического поля
сохраняется и в статической асимптотике. Логика построения систем полевых
уравнений для стационарных составляющих единого поля и анализ физического
содержания таких уравнений изложены в работе [13].
В итоге, имеем очевидное обобщение и серьезное развитие представлений классической электродинамики, согласно которым в Природе, так же как и в случае электромагнитного поля, не может быть электрического, магнитного или другой составляющей единого электродинамического поля с одной полевой компонентой. Структура обсуждаемых составляющих единого электродинамического поля из двух векторных взаимно ортогональных полевых компонент – это объективно необходимый способ их реального существования, принципиальная и единственная возможность распространения конкретной составляющей в виде потока соответствующей физической величины, в случае динамических полей – посредством поперечных волн.
Для подтверждения физической адекватности проведенного здесь теоретического
анализа объективной реальности ниже представлены результаты экспериментов
автора по изучению необходимых условий возбуждения и распространения
электродинамических полей в металлах, отвечающие на два физически важных
вопроса: волны каких полей можно реально возбудить в металлах и каковы
частотные ограничения известного дисперсионного соотношения асимптотики
металлов ![]() [2] при длинах волн
[2] при длинах волн ![]() . Возбуждение полей в
металле производилось на частотах n =
50 - 50.103 Гц и
было возможным только с помощью магнитной антенны, так как импеданс ближней
зоны лишь у магнитного диполя сопоставим с импедансом металлической среды. Для
приема прошедшего через металл излучения также надо было использовать только
магнитную антенну, что говорит о наличии в принимаемом сигнале только составляющей
магнитного поля.
. Возбуждение полей в
металле производилось на частотах n =
50 - 50.103 Гц и
было возможным только с помощью магнитной антенны, так как импеданс ближней
зоны лишь у магнитного диполя сопоставим с импедансом металлической среды. Для
приема прошедшего через металл излучения также надо было использовать только
магнитную антенну, что говорит о наличии в принимаемом сигнале только составляющей
магнитного поля.
Для определения закона частотной дисперсии волнового числа перечной магнитной
волны в металле его действительная часть ![]() измерялась
по сдвигу фазы
измерялась
по сдвигу фазы ![]() колебаний волны
при ее прохождении в плоском слое толщиной d :
колебаний волны
при ее прохождении в плоском слое толщиной d : ![]() , а мнимая часть
, а мнимая часть ![]() - по затуханию амплитуды
волны. Поскольку в теории металлов хорошим приближением (правда, для
электромагнитных волн) является равенство
- по затуханию амплитуды
волны. Поскольку в теории металлов хорошим приближением (правда, для
электромагнитных волн) является равенство ![]() ,
то следует ожидать (это показано теоретически выше), что указанные измерения
этими способами будут давать такие же результаты и для магнитных волн.
,
то следует ожидать (это показано теоретически выше), что указанные измерения
этими способами будут давать такие же результаты и для магнитных волн.
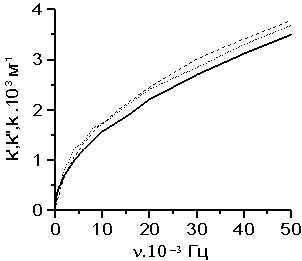 На рис. графически представлены результаты измерений
На рис. графически представлены результаты измерений ![]() по фазе (мелкие штрихи) и
по фазе (мелкие штрихи) и ![]() по затуханию (штрихи
крупнее) для медной пластинки толщиной d = 1,9 мм. Видно,
что измеренные данными способами частотные зависимости значений
по затуханию (штрихи
крупнее) для медной пластинки толщиной d = 1,9 мм. Видно,
что измеренные данными способами частотные зависимости значений ![]() и
и ![]() практически совпадают
(различия менее 5 %) и соответствуют формуле волнового числа для плоской
электродинамической волны в проводящей среде в асимптотике металлов
практически совпадают
(различия менее 5 %) и соответствуют формуле волнового числа для плоской
электродинамической волны в проводящей среде в асимптотике металлов ![]() при
при ![]() (сплошная линия).
(сплошная линия).
Однако оказалось,
что с понижением частоты значения мнимой части волнового числа ![]() сильно отклоняются от
значений действительной
сильно отклоняются от
значений действительной ![]() : в
медной пластинке на частотах
: в
медной пластинке на частотах ![]() 2.103
Гц и алюминия (d = 1,4 мм) при
2.103
Гц и алюминия (d = 1,4 мм) при ![]() 3.103
Гц. В области этих частот при их уменьшении, график
3.103
Гц. В области этих частот при их уменьшении, график ![]() переходит от обычного
переходит от обычного ![]() к линейной зависимости по
к линейной зависимости по ![]() и окончательно
и окончательно ![]() . Соответственно,
определяемая из
. Соответственно,
определяемая из ![]() частотная
зависимость скорости распространения волны в металле
частотная
зависимость скорости распространения волны в металле ![]() сначала ведет себя обычно
сначала ведет себя обычно ![]() , но при понижении частоты
переходит к
, но при понижении частоты
переходит к ![]() const и затем окончательно
const и затем окончательно ![]() .
Абсолютный минимум значений скорости для пластинки меди был ~ 14 м/с, а алюминия
~ 22 м/с.
.
Абсолютный минимум значений скорости для пластинки меди был ~ 14 м/с, а алюминия
~ 22 м/с.
Отклонение
характера частотных зависимостей волнового числа ![]() и
скорости
и
скорости ![]() от обычных
от обычных ![]() определяется толщиной
проводящего слоя: в толстых пластинках это изменение наступает на меньших
частотах, а в тонких – на более высоких частотах. Поскольку на фиксированной
частоте величина
определяется толщиной
проводящего слоя: в толстых пластинках это изменение наступает на меньших
частотах, а в тонких – на более высоких частотах. Поскольку на фиксированной
частоте величина ![]() является
константой материала и не может зависеть от толщины слоя, то наблюдаемый эффект
отклонения от закона дисперсии
является
константой материала и не может зависеть от толщины слоя, то наблюдаемый эффект
отклонения от закона дисперсии ![]() физически
обусловлен регистрацией структуры поля ближней зоны излучателя (согласно
измерениям, дипольного), проявляющей себя с понижением частоты.
физически
обусловлен регистрацией структуры поля ближней зоны излучателя (согласно
измерениям, дипольного), проявляющей себя с понижением частоты.
Таким образом, известная технология нагрева металлов с помощью магнитного индуктора, как мы теперь убедились теоретически и показали в эксперименте – это применение физического процесса возбуждения в проводящей среде чисто магнитных поперечных волн. Кстати, об открытии магнитных поперечных волн уже более 20 лет назад официально заявил Докторович, о чем он с удивительным упорством, достойным лучшего применения, безуспешно пытается втолковать другим, ссылаясь на свою статью [14]. Печально, но Высший судия - только Время, оно все расставит по своим местам! Резюме: если Вы сделали открытие, то загляните в книгу, там об этом уже все написано.
В заключение следует сказать, что в настоящей работе отсутствует обычная в таких случаях претензия на научную новизну, поскольку в ней представлен лишь краткий обзор, по сути дела, реферат уже опубликованных в печати некоторых важных результатов по изучению роли и места электромагнитного векторного потенциала в теории электричества, проводимого автором на протяжении ряда лет. Главная цель здесь была другая: указать пути выхода электромагнитной теории из застоя. Как представляется, нам это удалось, поскольку мы смогли выявить действительно новые реалии в физическом содержании уравнений Максвелла, проиллюстрировать подлинное их величие и грандиозные скрытые возможности в отношении полноты охвата наблюдаемых в Природе явлений электромагнетизма, в итоге тем самым провести модернизацию концептуальных представлений классической электродинамики о структуре и свойствах электромагнитного поля, которое является только лишь одной из равноправных взаимосвязанных составляющих векторного четырехкомпонентного единого электродинамического поля.
Литература:
1. Максвелл Дж. К. Трактат об электричестве и магнетизме. Т. I и II. М.: Наука, 1989.
2. Матвеев А.Н. Электродинамика. М.: Высшая школа, 1980.
3. Соколов И.В. // УФН. 1991. Т. 161. № 10. С. 175-190.
4. Антонов Л.И., Миронова Г.А., Лукашёва Е.В., Чистякова Н.И. Векторный магнитный потенциал в курсе общей физики. / Препринт № 11. М.: Изд. Физ. ф-та МГУ, 1998.
5. Кропп В. Патент РФ № 2101842.
6. Сидоренков В.В. // Вестник МГТУ им. Н.Э. Баумана. Сер. Естественные науки. 2005. № 2. С. 35-46; http://revolution./physics/00021495.html .
7. Сидоренков В.В. // http://revolution./physics/00023052.html
8. Сидоренков В.В. // Вестник МГТУ им. Н.Э. Баумана. Сер. Естественные науки. 2006. № 1. С. 28-37; http://revolution./physics/00021494.html.
9. Сидоренков В.В. // http://revolution./physics/00022974.html
10. Дюдкин Д.А., Комаров А.А. Электродинамическая индукция. Новая концепция геомагнетизма. / Препринт НАНУ, ДонФТИ-01-01, 2001.
11. Сидоренков В.В., Толмачев В.В., Федотова С.В. // Изв. РАН. Сер. физич. 2001. Т. 65. № 12. C. 1776-1782.
12. Чирков А.Г., Агеев А.Н. // ФТТ. 2002. Т. 44. Вып. 1. С. 3-5; 2007. Т. 49. Вып. 7. С. 1217-1221.
13. Сидоренков В.В. // http://revolution./physics/00021856.html
14. Докторович З.И. // http://www.sciteclibrary.ru/rus/catalog/pages/4797.html/