
Рефераты по авиации и космонавтике
Рефераты по административному праву
Рефераты по безопасности жизнедеятельности
Рефераты по арбитражному процессу
Рефераты по архитектуре
Рефераты по астрономии
Рефераты по банковскому делу
Рефераты по сексологии
Рефераты по информатике программированию
Рефераты по биологии
Рефераты по экономике
Рефераты по москвоведению
Рефераты по экологии
Краткое содержание произведений
Рефераты по физкультуре и спорту
Топики по английскому языку
Рефераты по математике
Рефераты по музыке
Остальные рефераты
Рефераты по биржевому делу
Рефераты по ботанике и сельскому хозяйству
Рефераты по бухгалтерскому учету и аудиту
Рефераты по валютным отношениям
Рефераты по ветеринарии
Рефераты для военной кафедры
Рефераты по географии
Рефераты по геодезии
Рефераты по геологии
Рефераты по геополитике
Рефераты по государству и праву
Рефераты по гражданскому праву и процессу
Рефераты по кредитованию
Рефераты по естествознанию
Рефераты по истории техники
Рефераты по журналистике
Рефераты по зоологии
Рефераты по инвестициям
Рефераты по информатике
Исторические личности
Рефераты по кибернетике
Рефераты по коммуникации и связи
Рефераты по косметологии
Рефераты по криминалистике
Рефераты по криминологии
Рефераты по науке и технике
Рефераты по кулинарии
Рефераты по культурологии
Рефераты по авиации и космонавтике
Рефераты по административному праву
Рефераты по безопасности жизнедеятельности
Рефераты по арбитражному процессу
Рефераты по архитектуре
Рефераты по астрономии
Рефераты по банковскому делу
Рефераты по сексологии
Рефераты по информатике программированию
Рефераты по биологии
Рефераты по экономике
Рефераты по москвоведению
Рефераты по экологии
Краткое содержание произведений
Рефераты по физкультуре и спорту
Топики по английскому языку
Рефераты по математике
Рефераты по музыке
Остальные рефераты
Рефераты по биржевому делу
Рефераты по ботанике и сельскому хозяйству
Рефераты по бухгалтерскому учету и аудиту
Рефераты по валютным отношениям
Рефераты по ветеринарии
Рефераты для военной кафедры
Рефераты по географии
Рефераты по геодезии
Рефераты по геологии
Рефераты по геополитике
Рефераты по государству и праву
Рефераты по гражданскому праву и процессу
Рефераты по кредитованию
Рефераты по естествознанию
Рефераты по истории техники
Рефераты по журналистике
Рефераты по зоологии
Рефераты по инвестициям
Рефераты по информатике
Исторические личности
Рефераты по кибернетике
Рефераты по коммуникации и связи
Рефераты по косметологии
Рефераты по криминалистике
Рефераты по криминологии
Рефераты по науке и технике
Рефераты по кулинарии
Рефераты по культурологии
Контрольная работа: Группировка коммерческих банков РФ по экономически чувствительным показателям
Контрольная работа: Группировка коммерческих банков РФ по экономически чувствительным показателям
КОНТРОЛЬНАЯ РАБОТА №1
Задача 1
По данным Приложения 1 произведите группировку 30-ти коммерческих банков РФ (в зависимости от Вашего варианта) по величине:
a) уставного фонда;
б) активов-нетто.
Каждую группу охарактеризуйте тремя наиболее экономически чувствительными показателями, имеющимися в приложение 1 . Наряду с абсолютными размерами показателей, приведите относительные величины структуры.
Результаты группировки изложите в сводных групповых таблицах и проанализируете.
Постройте гистограмму распределения банков по рассмотренным признакам.
Таблица 1.1
Список крупнейших банков России по размеру уставного фонда (на 1. 03.2000 г., млн. долл.)
| № | Наименование | № регис- трации | Возраст | Активы- нетто | Уставный фонд | Текущая прибыль | Капитал |
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| 41 | Мосфильмбанк | 3163 | 5 | 1,68 | 1,43 | 0,01 | 1,46 |
| 42 | Корвет | 2508 | 6 | 2,81 | 1,40 | 0,01 | 1,51 |
| 43 | Метрополь | 1639 | 8 | 21,84 | 1,39 | 0,07 | 2,63 |
| 44 | Алмаззолото | 3196 | 5 | 7,38 | 1,26 | 0,02 | 1,72 |
| 45 | Дзержинский | 1013 | 9 | 9,82 | 1,26 | 0,02 | 1,50 |
| 46 | Капиталъ-экспресс | 3036 | 5 | 4,26 | 1,26 | 0,01 | 1,64 |
| 48 | Оптбанк | 3138 | 5 | 4,61 | 1,22 | 0,07 | 1,36 |
| 49 | Межрегиональн. Почтовый | 3171 | 5 | 3,32 | 1,20 | 0,00 | 1,21 |
| 50 | Курганпромбанк | 1218 | 9 | 2,33 | 1,15 | 0,02 | 1,49 |
| № | Наименование | № регис- трации |
Возраст, лет |
Активы- нетто | Уставный фонд | Текущая прибыль | Капитал |
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| 51 | Мико-банк | 3195 | 5 | 3,08 | 1,14 | 0,05 | 1,35 |
| 52 | Москва. Центр | 2469 | 6 | 15,14 | 1,06 | 0,34 | 1,61 |
| 53 | ВУЗ-банк | 1712 | 7 | 7,12 | 1,05 | 0,04 | 1,78 |
| 54 | Новый Московский | 2932 | 5 | 1,68 | 1,03 | 0,01 | 1,42 |
| 55 | Мечел-банк | 419 | 9 | 4,60 | 0,92 | 0,07 | 1,41 |
| 56 | БМБ | 1871 | 7 | 2,20 | 0,88 | 0,04 | 1,46 |
| 57 | Воквнешторг-банк | 312 | 9 | 20,21 | 0,87 | 0,09 | 3,65 |
| 58 | Европейский | 1616 | 8 | 7,74 | 0,87 | 0,01 | 1,57 |
| 59 | Башкирский железнодор. | 2782 | 5 | 2,72 | 0,84 | 0,04 | 1,10 |
| 60 | Инстройбанк | 2743 | 5 | 1,59 | 0,77 | 0,02 | 0,94 |
| 61 | Курскпромбанк | 735 | 9 | 22,37 | 0,77 | 0,16 | 3,89 |
| 62 | Диам-банк | 2075 | 7 | 1,42 | 0,72 | 0,06 | 0,78 |
| 63 | Автогазбанк | 1713 | 9 | 12,61 | 0,69 | 0,25 | 2,74 |
| 64 | Екатеринбург | 3161 | 5 | 10,26 | 0,69 | 0,00 | 087 |
| 65 | МКБ им. Сергея Живаго | 2065 | 7 | 6,12 | 0,65 | 0,01 | 1,08 |
| 66 | Донкомбанк | 492 | 9 | 5,27 | 0,63 | 0,04 | 1,08 |
| 67 | Вербанк | 2374 | 6 | 7,33 | 0,61 | 0,04 | 2,90 |
| 68 | Зернобанк | 2337 | 6 | 6,30 | 0,61 | 0,10 | 1,13 |
| 69 | Национальный торговый | 3087 | 5 | 22,67 | 0,56 | 0,03 | 0,94 |
| 70 | АКИБ Пионер банк (ЗАО) | 3108 | 5 | 3,42 | 0,52 | 0,03 | 1,92 |
Решение:
1. Произведем группировку 29 коммерческих банков РФ по величине уставного фонда.
При образовании групп с равными интервалами, величина интервала определяется по формуле:
![]()
где Xmax и Xmin - максимальное и минимальное значение признака соответственно,
n - число групп.
| Интервал | Кол-во банков |
| 0,52-0,702 | 8 |
| 0,702-0,884 | 7 |
| 0,884-1,066 | 4 |
| 1,066-1,248 | 4 |
| 1,248-1,43 | 6 |
| Сумма | 29 |
Таблица 1.2
Группировка коммерческих банков по величине уставного капитала, млн. руб.
| № |
Группы банков по велич. УК, млн. руб. |
Наименование банка |
Возраст, лет |
Капитал |
Чистые активы |
Уставный фонд |
Прибыль/ убыток |
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| 1 | 0,52-0,702 | Автогазбанк | 9 | 2,74 | 12,61 | 0,69 | 0,25 |
| Екатеринбург | 5 | 0,87 | 10,26 | 0,69 | 0,00 | ||
| МКБ им. Сергея Живаго | 7 | 1,08 | 6,12 | 0,65 | 0,01 | ||
| Донкомбанк | 9 | 1,08 | 5,27 | 0,63 | 0,04 | ||
| Вербанк | 6 | 2,90 | 7,33 | 0,61 | 0,04 | ||
| Зернобанк | 6 | 1,13 | 6,30 | 0,61 | 0,10 | ||
| Национальный торговый | 5 | 0,94 | 22,67 | 0,56 | 0,03 | ||
| АКИБ Пионер банк (ЗАО) | 5 | 1,92 | 3,42 | 0,52 | 0,03 | ||
| ИТОГО | 8 | - | 12,66 | 73,98 | 4,96 | 0,5 | |
| 2 | 0,702-0,884 | БМБ | 7 | 1,46 | 2,20 | 0,88 | 0,04 |
| Воквнешторгбанк | 9 | 3,65 | 20,21 | 0,87 | 0,09 | ||
| Европейский | 8 | 1,57 | 7,74 | 0,87 | 0,01 | ||
| Башкирский железнодор. | 5 | 1,10 | 2,72 | 0,84 | 0,04 | ||
| Инстройбанк | 5 | 0,94 | 1,59 | 0,77 | 0,02 | ||
| Курскпромбанк | 9 | 3,89 | 22,37 | 0,77 | 0,16 | ||
| Диам-банк | 7 | 0,78 | 1,42 | 0,72 | 0,06 | ||
| ИТОГО | 7 | - | 13,39 | 58,25 | 5,72 | 0,42 | |
| 3 | 0,884-1,066 | Москва. Центр | 6 | 1,61 | 15,14 | 1,06 | 0,34 |
| ВУЗ-банк | 7 | 1,78 | 7,12 | 1,05 | 0,04 | ||
| Новый Московский | 5 | 1,42 | 1,68 | 1,03 | 0,01 | ||
| Мечел-банк | 9 | 1,41 | 4,60 | 0,92 | 0,07 | ||
| ИТОГО | 4 | - | 6,22 | 28,54 | 4,06 | 0,46 | |
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| 4 | 1,066-1,248 | ||||||
| Оптбанк | 5 | 1,36 | 4,61 | 1,22 | 0,07 | ||
| Межрегиональн. Почтовый | 5 | 1,21 | 3,32 | 1,20 | 0,00 | ||
| Курганпромбанк | 9 | 1,49 | 2,33 | 1,15 | 0,02 | ||
| Мико-банк | 5 | 1,35 | 3,08 | 1,14 | 0,05 | ||
| ИТОГО | 4 | - | 5,41 | 13,34 | 4,71 | 0,14 | |
| 5 | 1,248-1,43 | Мосфильмбанк | 5 | 1,46 | 1,68 | 1,43 | 0,01 |
| Корвет | 6 | 1,51 | 2,81 | 1,40 | 0,01 | ||
| Метрополь | 8 | 2,63 | 21,84 | 1,39 | 0,07 | ||
| Алмаззолото | 5 | 1,72 | 7,38 | 1,26 | 0,02 | ||
| Дзержинский | 9 | 1,50 | 9,82 | 1,26 | 0,02 | ||
| Капиталъ-экспресс | 5 | 1,64 | 4,26 | 1,26 | 0,01 | ||
| ИТОГО | 6 | - | 10,46 | 47,79 | 8,0 | 0,14 | |
| ВСЕГО | 29 | - | 48,14 | 221,9 | 27,45 | 1,66 |
Таблица 1.3
Сводная группировка коммерческих банков по величине уставного капитала, млн. руб.
| № |
Группы банков по величине УК, млн. руб. |
Кол-во банков |
Капитал |
Чистые активы |
Уставный фонд |
Прибыль/ убыток |
||||
|
млн. руб. |
% к итогу |
млн. руб. |
% к итогу |
млн. руб. |
% к итогу |
млн. руб. |
% к итогу |
|||
| 1 | 0,52-0,702 | 8 | 12,66 | 26,29 | 73,98 | 33,34 | 4,96 | 18,07 | 0,5 | 30,12 |
| 2 | 0,702-0,884 | 7 | 13,39 | 27,82 | 58,25 | 26,25 | 5,72 | 20,84 | 0,42 | 25,31 |
| 3 | 0,884-1,066 | 4 | 6,22 | 12,92 | 28,54 | 12,86 | 4,06 | 14,79 | 0,46 | 27,71 |
| 4 | 1,066-1,248 | 4 | 5,41 | 11,24 | 13,34 | 6,01 | 4,71 | 17,16 | 0,14 | 8,43 |
| 5 | 1,248-1,43 | 6 | 10,46 | 21,73 | 47,79 | 21,54 | 8,0 | 29,14 | 0,14 | 8,43 |
| ИТОГО | 29 | 48,14 | 100 | 221,9 | 100 | 27,45 | 100 | 1,66 | 100 | |
Вывод: из проанализированных 29 банков – 6 банков имеют наибольшую величину уставного фонда в пределах от 1,248 до 1,43 млн. рублей, на их долю приходится 11,46% всего капитала. По величине чистых активов (61,04% всего объема) преобладают банки с уставным фондом в пределах от 1,066 до 1,248 млн. рублей (5 банков), на их долю приходится 53,2 % всего капитала.
Гистограмма распределения банков по величине уставного капитала
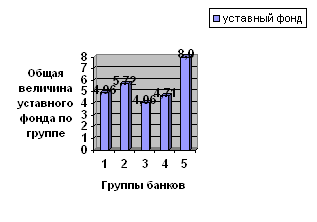
Рисунок 1.
2. Произведем группировку 29 коммерческих банков РФ по величине чистых активов.
Найдем величину интервала для преобразования групп с равными интервалами по формуле:
![]()
| Интервал | Кол-во банков |
| 1,42-5,67 | 15 |
| 5,67-9,92 | 7 |
| 9,92-14,17 | 2 |
| 14,17-18,42 | 1 |
| 18,42-22,67 | 4 |
| Сумма | 29 |
Таблица 1.4
Группировка коммерческих банков по величине чистых активов, млн. руб.
| № |
Группы банков по Величине чистых активов, млн. руб. |
Наименование банка |
Возраст, лет |
Капитал |
Чистые активы |
Уставный фонд |
Прибыль/ убыток |
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| 1 | 1,42-5,67 | ||||||
| АКИБ Пионер банк (ЗАО) | 5 | 1,92 | 3,42 | 0,52 | 0,03 | ||
| БМБ | 7 | 1,46 | 2,20 | 0,88 | 0,04 | ||
| Донкомбанк | 9 | 1,08 | 5,27 | 0,63 | 0,04 | ||
| Башкирский железнодор. | 5 | 1,10 | 2,72 | 0,84 | 0,04 | ||
| Инстройбанк | 5 | 0,94 | 1,59 | 0,77 | 0,02 | ||
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| Диам-банк | 7 | 0,78 | 1,42 | 0,72 | 0,06 | ||
| Новый Московский | 5 | 1,42 | 1,68 | 1,03 | 0,01 | ||
| Мечел-банк | 9 | 1,41 | 4,60 | 0,92 | 0,07 | ||
| Оптбанк | 5 | 1,36 | 4,61 | 1,22 | 0,07 | ||
| Межрегиональн. Почтовый | 5 | 1,21 | 3,32 | 1,20 | 0,00 | ||
| Курганпромбанк | 9 | 1,49 | 2,33 | 1,15 | 0,02 | ||
| Мико-банк | 5 | 1,35 | 3,08 | 1,14 | 0,05 | ||
| Мосфильмбанк | 5 | 1,46 | 1,68 | 1,43 | 0,01 | ||
| Корвет | 6 | 1,51 | 2,81 | 1,40 | 0,01 | ||
| Капиталъ-экспресс | 5 | 1,64 | 4,26 | 1,26 | 0,01 | ||
| ИТОГО | 15 | - | 20,13 | 44,99 | 15,11 | 0,48 | |
| 2 | 5,67-9,92 | ||||||
| МКБ им. Сергея Живаго | 7 | 1,08 | 6,12 | 0,65 | 0,01 | ||
| Зернобанк | 6 | 1,13 | 6,30 | 0,61 | 0,10 | ||
| Европейский | 8 | 1,57 | 7,74 | 0,87 | 0,01 | ||
| ВУЗ-банк | 7 | 1,78 | 7,12 | 1,05 | 0,04 | ||
| Алмаззолото | 5 | 1,72 | 7,38 | 1,26 | 0,02 | ||
| Дзержинский | 9 | 1,50 | 9,82 | 1,26 | 0,02 | ||
| Вербанк | 6 | 2,90 | 7,33 | 0,61 | 0,04 | ||
| ИТОГО | 7 | - | 11,68 | 51,81 | 6,31 | 0,24 | |
| 3 | 9,92-14,17 | ||||||
| Автогазбанк | 9 | 2,74 | 12,61 | 0,69 | 0,25 | ||
| Екатеринбург | 5 | 0,87 | 10,26 | 0,69 | 0,00 | ||
| ИТОГО | 2 | - | 3,61 | 22,87 | 1,38 | 0,25 | |
| 4 | 14,17-18,42 | ||||||
| Москва. Центр | 6 | 1,61 | 15,14 | 1,06 | 0,34 | ||
| ИТОГО | 1 | - | 1,61 | 15,14 | 1,06 | 0,34 | |
| 5 | 18,42-22,67 | ||||||
| Национальный торговый | 5 | 0,94 | 22,67 | 0,56 | 0,03 | ||
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| Воквнешторгбанк | 9 | 3,65 | 20,21 | 0,87 | 0,09 | ||
| Курскпромбанк | 9 | 3,89 | 22,37 | 0,77 | 0,16 | ||
| Метрополь | 8 | 2,63 | 21,84 | 1,39 | 0,07 | ||
| ИТОГО | 4 | - | 11,11 | 87,09 | 3,59 | 0,35 | |
| ВСЕГО | 29 | - | 48,14 | 221,9 | 27,45 | 1,66 |
Таблица 1.5
Сводная группировка коммерческих банков по величине чистых активов, млн. руб.
| № |
Группы банков по величине чистых активов, млн. руб. |
Кол-во банков |
Капитал |
Чистые активы |
Уставный фонд |
Прибыль/ убыток |
||||
|
млн. руб. |
% к итогу |
млн. руб. |
% к итогу |
млн. руб. |
% к итогу |
млн. руб. |
% к итогу |
|||
| 1 | 1,42-5,67 | 15 | 20,13 | 41,82 | 44,99 | 20,27 | 15,11 | 55,05 | 0,48 | 28,92 |
| 2 | 5,67-9,92 | 7 | 11,68 | 24,26 | 51,81 | 23,35 | 6,31 | 22,99 | 0,24 | 14,46 |
| 3 | 9,92-14,17 | 2 | 3,61 | 7,49 | 22,87 | 10,31 | 1,38 | 5,03 | 0,25 | 15,06 |
| 4 | 14,17-18,42 | 1 | 1,61 | 3,34 | 15,14 | 6,82 | 1,06 | 3,86 | 0,34 | 20,48 |
| 5 | 18,42-22,67 | 4 | 11,11 | 23,08 | 87,09 | 39,25 | 3,59 | 13,07 | 0,35 | 21,08 |
| ИТОГО | 29 | 48,14 | 100 | 221,9 | 100 | 27,45 | 100 | 1,66 | 100 | |
Вывод: из проанализированных 29 банков в основном преобладают малые банки (15 банков) с величиной чистых активов не более 44,99 млн. рублей, на долю которых приходится 20,27% всего капитала и 55,05% уставного фонда.
Гистограмма распределения банков по величине уставного капитала
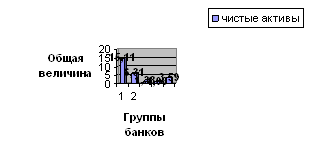
Рисунок 2.
Задача №2
Произведите комбинационную группировку коммерческих банков по двум признакам: возрасту и величине капитала.
Проанализируйте полученную группировку.
Решение:
1. Найдем величину интервала для группировки банков по возрасту:
![]()
| Номер группы | Интервал |
| 1 | 5,0-5,8 |
| 2 | 5,8-6,6 |
| 3 | 6,6-7,4 |
| 4 | 7,4-8,2 |
| 5 | 8,2-9,0 |
2. Найдем величину интервала для группировки банков по величине капитала:
![]()
| Номер группы | Интервал |
| 1 | 0,78-1,402 |
| 2 | 1,402-2,024 |
| 3 | 2,024-2,646 |
| 4 | 2,646-3,268 |
| 5 | 3,268-3,89 |
Таблица 2.1.
Группировка коммерческих банков по возрасту величине капитала
| № |
Группы банков по возрасту, лет |
В том числе подгруппы по величине капитала, млн. руб. |
Число банков |
Капитал, млн. руб. |
Чистые активы, млн. руб. |
Уставный фонд, млн. руб. |
Прибыль/ убыток, млн. руб. |
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| 1 | 5,0-5,8 | 0,78-1,402 | 7 | 7,77 | 48,25 | 6,42 | 0,21 |
| 1,402-2,024 | 5 | 8,16 | 18,42 | 5,5 | 0,08 | ||
| 2,024-2,646 | - | - | - | - | - | ||
| 2,646-3,268 | - | - | - | - | - | ||
| 3,268-3,89 | - | - | - | - | - | ||
| ИТОГО ПО | ГРУППЕ | 12 | 15,93 | 66,67 | 11,92 | 0,29 | |
| 2 | 5,8-6,6 | 0,78-1,402 | 1 | 1,13 | 6,3 | 0,61 | 0,10 |
| 1,402-2,024 | 2 | 3,12 | 17,95 | 2,46 | 0,35 | ||
| 2,024-2,646 | - | - | - | - | - | ||
| 2,646-3,268 | 1 | 2,9 | 7,33 | 0,63 | 0,04 | ||
| 3,268-3,89 | - | - | - | - | - | ||
| ИТОГО ПО | ГРУППЕ | 4 | 7,15 | 31,58 | 3,7 | 0,49 | |
| 3 | 6,6-7,4 | 0,78-1,402 | 2 | 1,86 | 7,54 | 1,37 | 0,07 |
| 1,402-2,024 | 2 | 3,24 | 9,32 | 1,93 | 0,08 | ||
| 2,024-2,646 | - | - | - | - | - | ||
| 2,646-3,268 | - | - | - | - | - | ||
| 3,268-3,89 | - | - | - | - | - | ||
| ИТОГО ПО | ГРУППЕ | 4 | 5,1 | 16,86 | 3,3 | 0,15 | |
| 4 | 7,4-8,2 | 0,78-1,402 | - | - | - | - | - |
| 1,402-2,024 | 1 | 1,57 | 7,74 | 0,87 | 0,01 | ||
| 2,024-2,646 | 1 | 2,63 | 21,84 | 1,39 | 0,07 | ||
| 2,646-3,268 | - | - | - | - | - | ||
| 3,268-3,89 | - | - | - | - | - | ||
| ИТОГО ПО | ГРУППЕ | 2 | 4,2 | 29,58 | 2,26 | 0,08 | |
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| 5 | 8,2-9,0 | 0,78-1,402 | 1 | 1,08 | 5,27 | 0,63 | 0,04 |
| 1,402-2,024 | 3 | 4,4 | 16,75 | 3,33 | 0,11 | ||
| 2,024-2,646 | - | - | - | - | - | ||
| 2,646-3,268 | 1 | 2,74 | 12,61 | 0,69 | 0,25 | ||
| 3,268-3,89 | 2 | 7,54 | 42,58 | 1,65 | 0,25 | ||
| ИТОГО ПО | ГРУППЕ | 7 | 15,76 | 77,21 | 6,3 | 0,65 | |
| ВСЕГО | 29 | 48,14 | 221,9 | 27,45 | 1,66 |
Вывод: проанализировав данную группировку можно сделать вывод о том, что преобладают банки в возрасте от 5,0 до 5,8 лет (12 банков), с величиной капитала от 0,78 до 1,402 млн. руб.
Задача №3
Постройте ряды распределения по 29 коммерческим банкам РФ:
а) по величине капитала;
б) по возрасту.
По полученным рядам распределения определите среднее, модальное и медианное значение каждого показателя.
Для графического изображения изучаемых вариационных рядов постройте гистограмму распределения (для интервального ряда) и полигон распределения (для дискретного ряда), а также кумулятивные кривые для изображения ряда накопленных частот.
Решение:
1. Построим ряд распределения банков по величине капитала:
Величина интервала:
![]()
Таблица 3.1
| № | Группы банков по величине капитала, млн. руб. |
Число банков, Fi |
Середина интервала, Xi |
Xi*Fi |
Сумма накопленных частот, S |
Xi-X | (Xi-X)*Fi | (Xi-X)2 | (Xi-X)2*Fi |
| 1 | 0,78-1,402 | 12 | 1,091 | 13,092 | 12 | 0,987 | 11,844 | 0,974 | 11,688 |
| 2 | 1,402-2,024 | 4 | 1,713 | 6,852 | 16 | 0,365 | 1,46 | 0,133 | 0,532 |
| 3 | 2,024-2,646 | 4 | 2,335 | 9,34 | 20 | 0,257 | 1,028 | 0,066 | 0,264 |
| 4 | 2,646-3,268 | 2 | 2,957 | 5,914 | 22 | 0,879 | 1,758 | 0,773 | 1,546 |
| 5 | 3,268-3,89 | 7 | 3,579 | 25,053 | 29 | 1,501 | 10,507 | 2,253 | 15,771 |
| ВСЕГО | 29 | - | 60,251 | - | - | 26,597 | - | 29,801 |
Среднее значение показателя рассчитывается как средняя арифметическая интервального ряда по формуле:
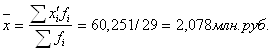
где ![]() середины интервалов;
середины интервалов; ![]() частота
частота ![]() го интервала.
го интервала.
Мода – значение признака, наиболее часто встречающееся в исследуемой совокупности, т.е. это одна из вариант признака, которая в ряду распределения имеет наибольшую частоту.
Модальным интервалом является 1-ый интервал с частотой Fmo=29
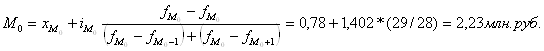
где ![]() нижняя граница
модального интервала;
нижняя граница
модального интервала;
![]() величина модального интервала,
величина модального интервала,
![]() частота модального интервала;
частота модального интервала;
![]() частота интервала, предшествующая
модальному;
частота интервала, предшествующая
модальному;
![]() частота интервала, следующего за
модальным.
частота интервала, следующего за
модальным.
Медиана – это варианта, которая находится в середине вариационного ряда.
Находим номер медианы: N=15,5
Медианный интервал находится в пределах 0,78-1,402 млн.руб.
Для нахождения медианы в интервальном вариационном ряду применяется формула:
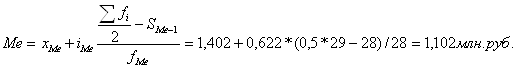
где ![]() нижняя граница
медианного интервала,
нижняя граница
медианного интервала,
![]() величина медианного интервала,
величина медианного интервала,
![]() сумма частот,
сумма частот,
![]() сумма накопленных частот,
предшествующих медианному интервалу,
сумма накопленных частот,
предшествующих медианному интервалу,
![]() частота медианного интервала.
частота медианного интервала.
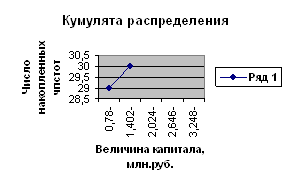
Рисунок 3.
2. Построим ряд распределения банков по возрасту.
Величина интервала: ![]()
Таблица 3.2
| № |
Группы банков по возрасту, лет |
Число банков, Fi |
Середина интервала, Xi |
Xi*Fi |
Сумма накопленных частот, S |
Xi-X | (Xi-X)*Fi | (Xi-X)2 | (Xi-X)2*Fi |
| 1 | 5,0-5,8 | 12 | 5,4 | 64,8 | 12 | 1,25 | 15 | 1,56 | 18,72 |
| 2 | 5,8-6,6 | 5 | 6,2 | 31,0 | 17 | 0,45 | 2,25 | 0,2 | 1,0 |
| 3 | 6,6-7,4 | 3 | 7,0 | 28,0 | 20 | 0,35 | 1,4 | 0,12 | 0,48 |
| 4 | 7,4-8,2 | 2 | 7,8 | 15,6 | 22 | 1,15 | 2,3 | 1,32 | 2,64 |
| 5 | 8,2-9,0 | 7 | 8,6 | 60,2 | 29 | 1,95 | 13,65 | 3,8 | 26,6 |
| ВСЕГО | 29 | - | 199,6 | - | - | 34,6 | - | 49,44 |
Среднее значение показателя рассчитывается как средняя арифметическая интервального ряда по формуле:
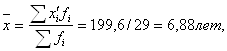
где ![]() середины интервалов;
середины интервалов;
![]() частота
частота ![]() го интервала.
го интервала.
Мода – значение признака, наиболее часто встречающееся в исследуемой совокупности, т.е. это одна из вариант признака, которая в ряду распределения имеет наибольшую частоту.
Модальным интервалом является 1-ый интервал с частотой Fmo=12
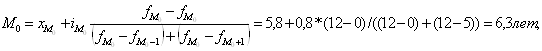
где ![]() нижняя граница
модального интервала;
нижняя граница
модального интервала;
![]() величина модального интервала,
величина модального интервала,
![]() частота модального интервала;
частота модального интервала;
![]() частота интервала, предшествующая
модальному;
частота интервала, предшествующая
модальному;
![]() частота интервала, следующего за
модальным.
частота интервала, следующего за
модальным.
Медиана – это варианта, которая находится в середине вариационного ряда.
Находим номер медианы: N=15,5
Медианный интервал находится в пределах 5,8-6,6 лет.
Для нахождения медианы в интервальном вариационном ряду применяется формула:
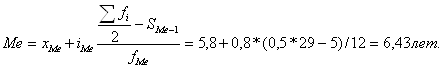
где ![]() нижняя граница
медианного интервала,
нижняя граница
медианного интервала,
![]() величина медианного интервала,
величина медианного интервала,
![]() сумма частот,
сумма частот,
![]() сумма накопленных частот,
предшествующих медианному интервалу,
сумма накопленных частот,
предшествующих медианному интервалу,
![]() частота медианного интервала.
частота медианного интервала.
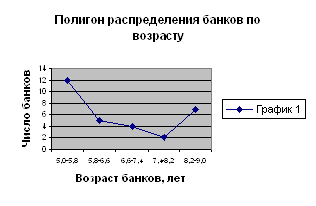
Рисунок 4.
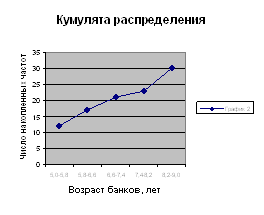
Рисунок 5.
Задача №4.
По построенным в задаче 3 рядам распределения рассчитайте:
а) размах вариации;
б) среднее линейное отклонение;
в) среднее квадратичное отклонение;
г) коэффициент вариации.
Расчеты показателей оформите в табличной форме.
Проанализируйте полученные результаты.
Решение:
Для расчета показателей вариации используем расчетные данные, представленные в таблицах 3.1 и 3.2.
1.Размах вариации представляет собой абсолютную разность между максимальным и минимальным значениями признака в изучаемой совокупности и вычисляется по формуле:
а) ![]()
б) ![]()
2.Среднее линейное отклонение вычисляется как взвешенное по частоте отклонение по модулю середин интервалов от средней арифметической величины:
а) 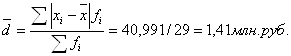
б) 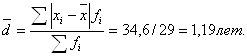
Наиболее широко используются в статистической практике и являются общепринятыми мерами вариации показатели дисперсии и среднего квадратического отклонения.
Дисперсия представляет собой средний квадрат отклонений индивидуальных значений признака (для данного примера – середин интервалов) от их средней величины. Расчет дисперсии производится по формуле:
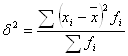 ;
;
3. Корень квадратный из дисперсии называется средним квадратическим отклонением:
а) 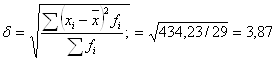
б) 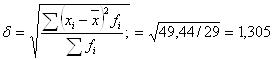
4. Коэффициент вариации – это относительный показатель вариации, равный процентному отношению среднего квадратического отклонения к средней арифметической:
а) ![]()
б) ![]()
Вывод: рассчитанная величина коэффициента вариации по двум рядам распределения свидетельствует: а) в первом случае – о высоком уровне колеблемости признака (т.к. рассчитанный коэффициент имеет высокое значение); б) во втором случае – о незначительном уровне колеблемости признака. Данные совокупности считаются неоднородными.
Задача №5
По данным задачи №1 проведите 20-процентную механическую выборку банков по величине капитала. Результаты представьте в таблице.
Установите:
а) средний размер капитала банков по выборке;
б) величину ошибки при определении величины капитала на основе выборки;
в) вероятные пределы колебания величины капитала для всех банков при вероятности 0,954.
Решение:
Таблица 5.1
Выборка коммерческих банков по величине уставного капитала, млн. руб.
| № |
Группы банков по велич. УК, млн. руб. |
Наименование банка |
Возраст, лет |
Капитал |
Чистые активы |
Уставный фонд |
Прибыль/ убыток |
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| Автогазбанк | 9 | 2,74 | 12,61 | 0,69 | 0,25 | ||
| Донкомбанк | 9 | 1,08 | 5,27 | 0,63 | 0,04 | ||
| Вербанк | 6 | 2,90 | 7,33 | 0,61 | 0,04 | ||
| Зернобанк | 6 | 1,13 | 6,30 | 0,61 | 0,10 | ||
| БМБ | 7 | 1,46 | 2,20 | 0,88 | 0,04 | ||
| Европейский | 8 | 1,57 | 7,74 | 0,87 | 0,01 | ||
| Инстройбанк | 5 | 0,94 | 1,59 | 0,77 | 0,02 | ||
| Курскпромбанк | 9 | 3,89 | 22,37 | 0,77 | 0,16 | ||
| Диам-банк | 7 | 0,78 | 1,42 | 0,72 | 0,06 | ||
| Москва. Центр | 6 | 1,61 | 15,14 | 1,06 | 0,34 | ||
| ВУЗ-банк | 7 | 1,78 | 7,12 | 1,05 | 0,04 | ||
| Новый Московский | 5 | 1,42 | 1,68 | 1,03 | 0,01 | ||
| Оптбанк | 5 | 1,36 | 4,61 | 1,22 | 0,07 | ||
| Курганпромбанк | 9 | 1,49 | 2,33 | 1,15 | 0,02 | ||
| Мико-банк | 5 | 1,35 | 3,08 | 1,14 | 0,05 | ||
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| Мосфильмбанк | 5 | 1,46 | 1,68 | 1,43 | 0,01 | ||
| Метрополь | 8 | 2,63 | 21,84 | 1,39 | 0,07 | ||
| Алмаззолото | 5 | 1,72 | 7,38 | 1,26 | 0,02 | ||
| Дзержинский | 9 | 1,50 | 9,82 | 1,26 | 0,02 | ||
| Капиталъ-экспресс | 5 | 1,64 | 4,26 | 1,26 | 0,01 | ||
| ВСЕГО | 20 | - | 34,54 | 145,77 | 19,8 | 1,38 |
1. Средний размер капитала банка по выборке:
![]()
2. Средняя ошибка выборки:
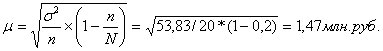 ,
,
где n и N - объем выборочной и генеральной совокупности соответственно.
δ² = ∑(хi-х)²/n = (34,54-1,727)²/20 = 53,83
3. Предельная ошибка (![]() ) определяется
умножением средней ошибки на коэффициент доверия t , определяемый в зависимости от уровня вероятности (он равен
2).
) определяется
умножением средней ошибки на коэффициент доверия t , определяемый в зависимости от уровня вероятности (он равен
2).
![]() = t* μ=2*1,47=2,94 млн.руб.
= t* μ=2*1,47=2,94 млн.руб.
4. Вероятные пределы колебания величины капитала:
![]()
1,727 - 2,94 ≤ χ ≤ 1,727 + 2,94
1,213 млн.руб.≤ χ ≤4,667млн.руб.