
Рефераты по авиации и космонавтике
Рефераты по административному праву
Рефераты по безопасности жизнедеятельности
Рефераты по арбитражному процессу
Рефераты по архитектуре
Рефераты по астрономии
Рефераты по банковскому делу
Рефераты по сексологии
Рефераты по информатике программированию
Рефераты по биологии
Рефераты по экономике
Рефераты по москвоведению
Рефераты по экологии
Краткое содержание произведений
Рефераты по физкультуре и спорту
Топики по английскому языку
Рефераты по математике
Рефераты по музыке
Остальные рефераты
Рефераты по биржевому делу
Рефераты по ботанике и сельскому хозяйству
Рефераты по бухгалтерскому учету и аудиту
Рефераты по валютным отношениям
Рефераты по ветеринарии
Рефераты для военной кафедры
Рефераты по географии
Рефераты по геодезии
Рефераты по геологии
Рефераты по геополитике
Рефераты по государству и праву
Рефераты по гражданскому праву и процессу
Рефераты по кредитованию
Рефераты по естествознанию
Рефераты по истории техники
Рефераты по журналистике
Рефераты по зоологии
Рефераты по инвестициям
Рефераты по информатике
Исторические личности
Рефераты по кибернетике
Рефераты по коммуникации и связи
Рефераты по косметологии
Рефераты по криминалистике
Рефераты по криминологии
Рефераты по науке и технике
Рефераты по кулинарии
Рефераты по культурологии
Рефераты по авиации и космонавтике
Рефераты по административному праву
Рефераты по безопасности жизнедеятельности
Рефераты по арбитражному процессу
Рефераты по архитектуре
Рефераты по астрономии
Рефераты по банковскому делу
Рефераты по сексологии
Рефераты по информатике программированию
Рефераты по биологии
Рефераты по экономике
Рефераты по москвоведению
Рефераты по экологии
Краткое содержание произведений
Рефераты по физкультуре и спорту
Топики по английскому языку
Рефераты по математике
Рефераты по музыке
Остальные рефераты
Рефераты по биржевому делу
Рефераты по ботанике и сельскому хозяйству
Рефераты по бухгалтерскому учету и аудиту
Рефераты по валютным отношениям
Рефераты по ветеринарии
Рефераты для военной кафедры
Рефераты по географии
Рефераты по геодезии
Рефераты по геологии
Рефераты по геополитике
Рефераты по государству и праву
Рефераты по гражданскому праву и процессу
Рефераты по кредитованию
Рефераты по естествознанию
Рефераты по истории техники
Рефераты по журналистике
Рефераты по зоологии
Рефераты по инвестициям
Рефераты по информатике
Исторические личности
Рефераты по кибернетике
Рефераты по коммуникации и связи
Рефераты по косметологии
Рефераты по криминалистике
Рефераты по криминологии
Рефераты по науке и технике
Рефераты по кулинарии
Рефераты по культурологии
Контрольная работа: Статистические задачи
Контрольная работа: Статистические задачи
ЗАДАЧА 1
По исходным данным вычислить основные аналитические показатели рядов динамики (по цепной и базисной схемам):
а) средний уровень ряда динамики;
б) абсолютный прирост;
в) темп роста;
г) темп прироста;
д) абсолютное значение 1% прироста;
е) средний темп роста и средний темп прироста.
Средний уровень интервального ряда определим по формуле:
![]()
где Yi – значение грузооборота;
n – число значений в динамическом ряду.
Абсолютный прирост относительно базисного уровня грузооборота определим по формуле:
ΔYi=Yi-Y0
Абсолютный прирост грузооборота относительно предшествующего года определим по формуле:
ΔYi=Yi-Yi-1
Темп роста относительно базисного уровня грузооборота определим по формуле:
![]()
Темп роста грузооборота относительно предшествующего года определим по формуле:
![]()
Темп прироста относительно базисного уровня грузооборота определим по формуле:
![]()
Темп прироста грузооборота относительно предшествующего года определим по формуле:
![]()
Средний темп роста грузооборота определим по формуле:
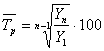
Средний темп прироста грузооборота определим по формуле:
![]()
Абсолютное значение одного процента прироста определим по формуле:
![]()
Результаты расчёта аналитических показателей ряда динамики представим в таблице 1.1
Таблица 1 – Основные аналитические показатели ряда динамики
| Показатель | Схема счета | Периоды | |||||||
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | ||
| Уровень ряда | 1199 | 1253 | 1573 | 1385 | 1276 | 1385 | 1266 | 1358 | |
| Средний уровень ряда | 1336,875 | ||||||||
| Абсолютный прирост | Базисная | 100 | 54,0 | 374,0 | 186,0 | 77,0 | 186 | 67 | 159 |
| Цепная | 100 | 54,0 | 320,0 | -188,0 | -109,0 | 109,0 | -119,0 | 92,0 | |
| Темп роста | Базисная | 100 | 104,5 | 131,2 | 115,5 | 106,4 | 115,5 | 105,6 | 113,3 |
| Цепная | 100 | 104,5 | 125,5 | 88,0 | 92,1 | 108,5 | 91,4 | 107,3 | |
| Темп прироста | Базисная | 100 | 4,5 | 31,2 | 15,5 | 6,4 | 15,5 | 5,6 | 13,3 |
| Цепная | 100 | 4,5 | 25,5 | -12,0 | -7,9 | 8,5 | -8,6 | 7,3 | |
| Абсолютное значение 1% прироста | 11,99 | 12,53 | 15,73 | 13,85 | 12,76 | 13,85 | 12,66 | ||
| Средний темп роста | 101,79 | ||||||||
| Средний темп прироста | 1,79 | ||||||||
Произведем сглаживание данных за три года при помощи двенадцатимесячной скользящей средней, централизованной на седьмой месяц. Рассчитаем коэффициент сезонности по данным трех лет, и построим график сезонной волны.
Сглаживание рядов динамики производится с помощью простых средних, скользящей средней, методами аналитического выравнивания. Скользящие средние рассчитываются по формулам:
![]() ;
;
![]() и т.д. - нецентрализованная
и т.д. - нецентрализованная
![]() - централизованная
- централизованная
Коэффициент сезонности определяется как отношение уровней ряда к их среднему уровню по формуле:
![]()
Средний коэффициент сезонности за рассматриваемый период находим по формуле:
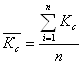
где n – количество рассчитанных коэффициентов сезонности по одноименным месяцам.
Расчет скользящей средней и коэффициента сезонности приведем в таблице 1.2.
Простроим график сезонной волны по средним коэффициентам сезонности. График приведен на рисунке 1.
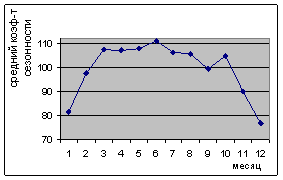
Рисунок 1 – График сезонной волны
Таблица 2 – Расчет коэффициента сезонности
| Год | Месяц | Уровень ряда | Скользящая средняя | Коэффициент сезонности | Средний коэффициент сезонности | |
| нецентрированная | центрированная | |||||
| 1994 | 1 | 21,1 | ||||
| 2 | 22,8 | |||||
| 3 | 23,9 | |||||
| 4 | 23,8 | |||||
| 5 | 24,5 | |||||
| 6 | 24,6 | 23,550 | ||||
| 7 | 25,9 | 23,492 | 23,521 | 104,016 | ||
| 8 | 25,7 | 23,617 | 23,554 | 103,213 | ||
| 9 | 24,2 | 23,783 | 23,700 | 97,189 | ||
| 10 | 25,5 | 23,942 | 23,863 | 102,410 | ||
| 11 | 22,3 | 24,067 | 24,004 | 89,558 | ||
| 12 | 18,3 | 24,217 | 24,142 | 73,494 | ||
| 1995 | 1 | 20,4 | 24,308 | 24,263 | 81,928 | 81,53 |
| 2 | 24,3 | 24,408 | 24,358 | 97,590 | 97,39 | |
| 3 | 25,9 | 24,500 | 24,454 | 104,016 | 107,23 | |
| 4 | 25,7 | 24,592 | 24,546 | 103,213 | 107,03 | |
| 5 | 26 | 24,608 | 24,600 | 104,418 | 107,83 | |
| 6 | 26,4 | 24,750 | 24,679 | 106,024 | 110,84 | |
| 7 | 27 | 24,733 | 24,742 | 108,434 | 106,22 | |
| 8 | 26,9 | 24,725 | 24,729 | 108,032 | 105,62 | |
| 9 | 25,3 | 24,858 | 24,792 | 101,606 | 99,40 | |
| 10 | 26,6 | 25,017 | 24,938 | 106,827 | 104,62 | |
| 11 | 22,5 | 25,158 | 25,088 | 90,361 | 89,96 | |
| 12 | 20 | 25,358 | 25,258 | 80,321 | 76,91 | |
| 1996 | 1 | 20,2 | 25,517 | 25,438 | 81,124 | |
| 2 | 24,2 | 25,942 | 25,729 | 97,189 | ||
| 3 | 27,5 | 26,325 | 26,133 | 110,442 | ||
| 4 | 27,6 | 26,367 | 26,346 | 110,843 | ||
| 5 | 27,7 | 26,467 | 26,417 | 111,245 | ||
| 6 | 28,8 | 26,400 | 26,433 | 115,663 | ||
| 7 | 28,9 | |||||
| 8 | 32 | |||||
| 9 | 29,9 | |||||
| 10 | 27,1 | |||||
| 11 | 23,7 | |||||
| 12 | 19,2 | |||||
| Итого: | 896,4 | |||||
| Средняя: | 24,90 | |||||
Из графика видно, что коэффициент сезонности в начале года увеличивается, а в конце - уменьшается. Наибольшее отклонение наблюдается в начале года 2-ой и 10 -ой месяц.
ЗАДАЧА 2
Произвести аналитическое выравнивание рядов динамики по данным задачи 1 о размерах грузооборота по родам грузов:
а) при равномерном развитии y = a0 + a1t ;
б) при развитии с переменным ускорением (замедлением) yt = a0 + a1t + a2t2 + a3t3 ;
в) при изучении сезонных колебаний по данным об отправлении грузов yt = a0 + (ak cosRt + bk sinRt) .
Результаты расчётов представить в виде таблиц и графиков.
1. Способ отсчета времени от условного начала, когда ∑t=0, дает возможность определить параметры математической функции по формулам:
![]()
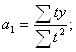
Результаты вычислений приведем в таблице 3:
Таблица 3 – Вычисление параметров функции y=a0+a1t и y=a0+a1t+a2t2+a3t3
| Год | t | y | t² | ty |
t4 |
t6 |
t²y | t³y | Yti* | Yt | (Yti*-y)² | (Yt-y)² |
| 1 | -4 | 1199 | 16 | 256 | 4096 | -4796 | 19184 | -76736 | 1324,2 | 1175,2 | 15677,13 | 566,75 |
| 2 | -3 | 1253 | 9 | 81 | 729 | -3759 | 11277 | -33831 | 1327,4 | 1354,3 | 5531,64 | 10254,93 |
| 3 | -2 | 1573 | 4 | 16 | 64 | -3146 | 6292 | -12584 | 1330,5 | 1432,5 | 58786,04 | 19730,33 |
| 4 | -1 | 1385 | 1 | 1 | 1 | -1385 | 1385 | -1385 | 1333,7 | 1438,1 | 2630,84 | 2817,52 |
| 5 | 1 | 1276 | 1 | 1 | 1 | 1276 | 1276 | 1276 | 1340,0 | 1343,3 | 4101,34 | 4532,35 |
| 6 | 2 | 1385 | 4 | 16 | 64 | 2770 | 5540 | 11080 | 1343,2 | 1299,2 | 1746,54 | 7364,77 |
| 7 | 3 | 1266 | 9 | 81 | 729 | 3798 | 11394 | 34182 | 1346,4 | 1294,6 | 6460,14 | 820,27 |
| 8 | 4 | 1358 | 16 | 256 | 4096 | 5432 | 21728 | 86912 | 1349,5 | 1357,8 | 71,54 | 0,05 |
| итого | 0 | 10695 | 60 | 708 | 9780 | 190 | 78076 | 8914 | 10695,0 | 10695,0 | 95005,21 | 46086,98 |
Тогда:
![]()
![]()
Уравнение при равномерном развитии:
y = 1336,88 - 3,17 ∙ t
2. Для вычисления параметров функции y=a0+a1t+a2t2+a3t3 :
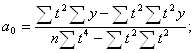
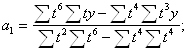
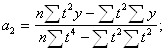
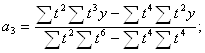
Тогда:
![]()
![]()
![]()
![]()
Уравнение при развитии с переменным ускорением (замедлением):
yt= 1398,98 - 52,06 t - 8,28 t2 + 4,68 t3;
3. По рассмотренным моделям определим теоретические уровни тренда. Фактические и теоретические уровни ряда нанесём на график, представленный на рисунке 2.
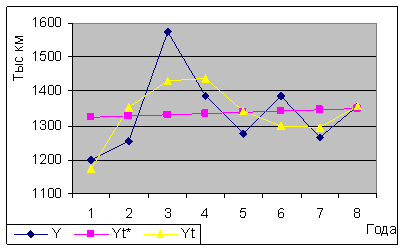
Рисунок 2 – График фактических и теоретических уровней ряда
Рассчитаем стандартизированную
ошибку аппроксимации – ![]()
![]()
![]()
![]()
4. При изучении сезонных
колебаний по данным об отправлении грузов ![]() необходимо
рассчитать параметры:
необходимо
рассчитать параметры:
![]()
![]()
![]()
Результаты расчётов сведём в таблицу 4
Таблица 4 – Выравнивание ряда динамики y=a0+(aкcosRt+ bкsinRt), 1998 год
| Месяц |
ti |
yi |
cos ti |
sin ti |
yi∙cos ti |
yi∙sin ti |
yti |
| 1 | 0 | 21,10 | 1 | 0 | 21,1 | 0 | 21,21 |
| 2 | (1:6)π | 22,80 | 0,86616 | 0,5 | 19,748 | 11,4 | 21,66 |
| 3 | (1:3) π | 23,90 | 0,5 | 0,866 | 11,95 | 20,6974 | 22,62 |
| 4 | (1:2) π | 23,80 | 0 | 1 | 0 | 23,8 | 23,82 |
| 5 | (2:3) π | 24,50 | -0,5 | 0,866 | -12,25 | 21,217 | 24,96 |
| 6 | (5:6) π | 24,60 | -0,866 | 0,5 | -21,3 | 12,3 | 25,71 |
| 7 | π | 25,90 | -1 | 0 | -25,9 | 0 | 25,89 |
| 8 | (7:6) π | 25,70 | -0,866 | -0,5 | -22,26 | -12,85 | 25,44 |
| 9 | (4:3) π | 24,20 | -0,5 | -0,866 | -12,1 | -20,9572 | 24,48 |
| 10 | (3:2) π | 25,50 | 0 | -1 | 0 | -25,5 | 23,28 |
| 11 | (5:3) π | 22,30 | 0,5 | -0,866 | 11,15 | -19,3118 | 22,14 |
| 12 | (11:6) π | 18,30 | 0,866 | -0,5 | 15,848 | -9,15 | 21,39 |
| - | 282,6 | -14,01 | 1,6454 | 282,60 |
![]()
![]()
![]()
![]()
Фактические и теоретические уровни ряда нанесём на график, представленный на рисунке 3.
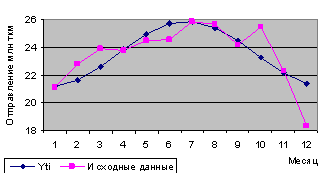
Рисунок 3 – График фактических и теоретических уровней ряда выравнивания
Фактические и теоретические уровни ряда близки по значению, а кривая ряда (рисунок 3) похожа на гармоническую функцию.
Поэтому функцию ![]() можно использовать для
выравнивания ряда динамики.
можно использовать для
выравнивания ряда динамики.
ЗАДАЧА 3
По данным таблицы определить:
1) выполнение норм удельного расхода топлива по отделениям и дороге в целом;
2) сводный индекс расхода топлива на дороге;
3) изменение среднего удельного расхода топлива на дороге за счет изменения удельного расхода топлива на 10000 т/км брутто на отделениях и за счет изменения структуры грузооборота по отделениям, а также за счет того и другого фактора одновременно;
4) абсолютный размер экономии (перерасхода) топлива за счет изменения грузооборота на отделениях, за счет изменения удельного расхода топлива на отделениях.
Таблица 10 – Грузооборот и удельный расход топлива по отделениям железной дороги
| Отделение | Удельный расход топлива, кг/10000 т·км брутто. | Грузооборот брутто, млн. т·км | Выполнение норм удельного расхода топлива, % | Расход топлива, тонн | |||||
| Норма | Факти-чески | Норма | Факти-чески | % выпол-нения | План | Факт | Отчетного по удельному расходу базисного | ||
| 1 | 50 | 47 | 200 | 113 | 56,5 | 94,0 | 10000 | 5311 | 5650 |
| 2 | 55 | 57 | 320 | 102 | 31,9 | 103,6 | 17600 | 5814 | 5610 |
| 3 | 48 | 45 | 400 | 101 | 25,3 | 93,8 | 19200 | 4545 | 4848 |
| 920 | 316 | 113,6 | 46800 | 15670 | 16108 | ||||
1) выполнение норм удельного расхода топлива по отделениям и дороги в целом
Iи=∑и1q1 / ∑и0q1 =15670 / 16108 = 0,973
2) Сводный индекс расхода топлива
Iиq=∑и1q1 / ∑и0q0 =15670 / 46800 = 0,335
3) Индекс удельного расхода топлива переменного состава
Iи = ∑и1q1/∑q1 : ∑и0q0/∑q0 = ∑и1q1/∑и0q1= 15670/316 : 46800/920 = 0,975
Индекс удельного расхода топлива постоянного состава
Iи=∑и1q1/∑q1 : ∑и0q1/∑q1= ∑и1q1/∑и0q1 = 15670 / 16108 = 0,973
Индекс структурных сдвигов
Iстр= ∑и0q1/∑q1 : ∑и0q0/∑q0 = 16108/316 : 46800/920 = 1,002
4) Экономия топлива за счет изменения удельного расхода
Δиq=∑и1q1-∑и0q1= 15670 - 16108 = -438 кг за счет изменения грузооборота
Δиqq=∑и0q1-∑и0q0= 16108 - 46800 = -30692 кг
ЗАДАЧА 4
№ 1. Для изучения производительности труда токарей на машиностроительном заводе было проведено 10%-ное выборочное обследование 100 рабочих методом случайного бесповторного отбора. В результате обследования получены данные о часовой выработке рабочих:
| Часовая выработка, шт. | 18-20 | 20-22 | 22-24 | 24-26 | 26-28 | 28-30 |
| Число рабочих | 2 | 8 | 24 | 50 | 12 | 4 |
С вероятностью 0,997 определите пределы, в которых находится среднее время обработки одной детали токарями завода.
Рассчитаем среднюю ошибку выборки по формуле:
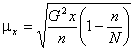
Дисперсия
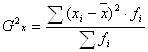
где хi - часовая выработка
![]() - средняя часовая выработка по
всем рабочим выборки;
- средняя часовая выработка по
всем рабочим выборки;
fi - сумма всех частот
| Часовая выработка, шт. | 18-20 | 20-22 | 22-24 | 24-26 | 26-28 | 28-30 | |
| Число рабочих | 2 | 8 | 24 | 50 | 12 | 4 | 100 |
|
|
40 | 176 | 576 | 1300 | 288 | 120 | 2500 |
|
(xi - |
-10 | -24 | -24 | 50 | 36 | 20 | 48 |
![]()
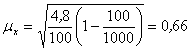
∆х = ± t · μx ∆х = ± 3 · 0,66 = 2 шт.
Ответ: с вероятностью 0,997 можно утверждать, что доля лиц, которая одобрит составит 54% - 66%.
1. Быченко О.Г. Общая теория статистики: Задание на контрольную работу № 1 с методическими указаниями. – Гомель: БелГУТ, 2000. – 30 с.
2. Быченко О.Г. Общая теория статистики: Задание на контрольную работу № 2 с методическими указаниями. – Гомель: БелГУТ, 2000. – 31 с.
3. Общая теория статистики: Учебник/Т.В. Рябушкин, М.Р. Ефимова, Н.И. Яковлева. – М.: Финансы и статистика, 1981. – 279 с., ил.