
Рефераты по авиации и космонавтике
Рефераты по административному праву
Рефераты по безопасности жизнедеятельности
Рефераты по арбитражному процессу
Рефераты по архитектуре
Рефераты по астрономии
Рефераты по банковскому делу
Рефераты по сексологии
Рефераты по информатике программированию
Рефераты по биологии
Рефераты по экономике
Рефераты по москвоведению
Рефераты по экологии
Краткое содержание произведений
Рефераты по физкультуре и спорту
Топики по английскому языку
Рефераты по математике
Рефераты по музыке
Остальные рефераты
Рефераты по биржевому делу
Рефераты по ботанике и сельскому хозяйству
Рефераты по бухгалтерскому учету и аудиту
Рефераты по валютным отношениям
Рефераты по ветеринарии
Рефераты для военной кафедры
Рефераты по географии
Рефераты по геодезии
Рефераты по геологии
Рефераты по геополитике
Рефераты по государству и праву
Рефераты по гражданскому праву и процессу
Рефераты по кредитованию
Рефераты по естествознанию
Рефераты по истории техники
Рефераты по журналистике
Рефераты по зоологии
Рефераты по инвестициям
Рефераты по информатике
Исторические личности
Рефераты по кибернетике
Рефераты по коммуникации и связи
Рефераты по косметологии
Рефераты по криминалистике
Рефераты по криминологии
Рефераты по науке и технике
Рефераты по кулинарии
Рефераты по культурологии
Курсовая работа: Уравновешивание геодезических сетей сгущения и систем ходов плановой съемочной сети
Курсовая работа: Уравновешивание геодезических сетей сгущения и систем ходов плановой съемочной сети
КАБИНЕТ МИНИСТРОВ УКРАИНЫ
ЮФ «Крымский агротехнологический университет» НАУ
Кафедра геодезии и землеустройства
Курсовой проект по геодезии
на тему: «Уравновешивание геодезических сетей сгущения и систем ходов плановой съемочной сети»
Выполнила: Гуськова А.Е.
Группа: К-21.1
Проверил: Нечаев В.А.
Симферополь 2006
1. Уравновешивание триангуляции 2 разряда
1.1 Предварительная математическая обработка измерений
1.1.1 Исходные данные
На рисунке 1 приведена схема триангуляции 2-го разряда. Пункт полигонометрии «Марьино» является пунктом геодезической сети высшего разряда Сторона между пунктами «Марьино» и «Луговое» является исходной.
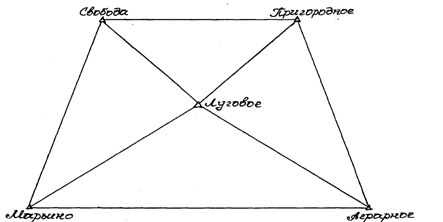
Рис 1. Схема триангуляции 2-го разряда
В таблице 1 представлены координаты опорного пункта «Марьино» и результаты полевых измерений длины исходной стороны и ее направления (α).
Таблица 1
| №№ | Название пункта | Координаты | Длина исходной стороны, м | Дирекционный угол, α | |
| Х | У | ||||
| 8 | Марьино | 5008,50 | 1000,0 | 1753,45 | 72028'50'' |
1.1.2 Порядок вычислений
Составить первую рабочую схему исполненной сети (рис. 2) на которую выписать из таблицы 2 измеренные направления.
На схеме намечаем исходную (твердую) сторону, пронумеровываем треугольники, обозначаем промежуточные стороны и углы.
Измеренные элементы приведения и направления Таблица 2
| Название пунктов | Элементы приведения | Название направлений | Измеренные направления |
| Аграрное | е=0,015м е1=0,060м | Луговое | 0000'00'' |
| Q=2130 на Луговое | Пригородное | 49020'53'' | |
| Q1=2930 на Луговое | Марьино | 325008'58'' | |
| Марьино | е = ─ е1=0,030м | Свобода | 0000'00'' |
| Q= ─ | Луговое | 81010'17'' | |
| Q1=2380 на Свободу | Аграрное | 109053'48'' | |
| Свобода | е= ─ е1=0,035м | Пригородное | 0000'00'' |
| Q= ─ | Луговое | 30033'34'' | |
| Q1=2410 на Пригородное | Марьино | 69059'13'' | |
| Луговое | е=0,030м е1=0,035м | Пригородное | 0000'00'' |
| Q1=1810 на Пригородное | Аграрное | 89027'38'' | |
| Q1=360 на Пригородное | Марьино | 205053'02'' | |
| Свобода | 265016'56'' | ||
| Пригородное | е=0,025м е1= ─ | Аграрное | 0000'00'' |
| Q1=1270 на Аграрное | Луговое | 41011'30'' | |
| Q1= ─ | Свобода | 95054'38'' |
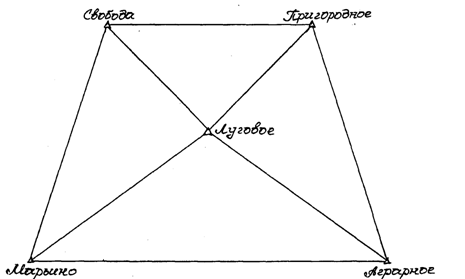
Рис 2. Рабочая схема 1 (углы измеренные)
По данным таблицы 2 вычисляем измеренные углы и выписываем их значения на рабочую схему (рис 2.)
Вычисленные значения углов выписываем с округлением до 1' в бланк предварительного решения треугольников в порядке нумерации, указанной в таблице 3. Длину исходной стороны выписываем с округлением до 10 м в одной строке с противоположным углом.
Подсчитываем сумму углов по каждому треугольнику. Если она отличается (за счет ошибок округления) от 180° не более чем 1', то находим синусы углов (с тремя десятичными знаками).
По теореме синусов вычисляем стороны треугольников, начиная с первого, по формулам:
ai=Di sin A bi=Di sin A ci=Di sin A
в которых Di - постоянный коэффициент для i треугольника, определяемый соотношением:
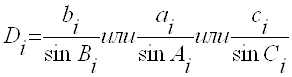 (2)
(2)
Контролем решения треугольников является сходимость длины исходной стороны bi с вычисленным значением a1. Расхождение не должно быть (для данной сети) более 10 метров, т.е. ∆ в= b1 - a4 ≤ 10 м (таблица 3).
В бланк вычисления поправок за центрировку и редукцию (таблица 4) выписать в соответствии со своим вариантом из таблицы 2 линейные и угловые элементы приведения. Цифрами в скобках указан порядок записи и решения.
В каждой графе таблицы 4 записываем название пункта по измеренному направлению, начиная с начального и в строку 5, в том же порядке выписываем из ведомости измеренных величин (таблица 2) значения измеренных направлений М.
Таблица 3
Предварительное решение треугольников
| № тр | Название пунктов | № углов | Углы | Синусы углов | Длины сторон |
| 1 | ДI =2760 | ||||
| Свобода | 2 | 39º26' | 0,635 | вI=1750вссссс | |
| Луговое | 3 | 59º24' | 0,861 | сI=2380 | |
| Марьино | 1 | 81º10' | 0,988 | аI=2730 | |
| 2 | ДII=3350 | ||||
| Пригородное | 5 | 54º43' | 0,816 | вII=2730 | |
| Луговое | 6 | 94º43' | 0,997 | сII=3340 | |
| Свобода | 4 | 30º34' | 0,509 | аII=1710 | |
| 3 | ДIII=2250 | ||||
| Аграрное | 8 | 49º21' | 0,759 | вIII=1710 | |
| Луговое | 9 | 89º28' | 1,000 | сIII=2250 | |
| Пригородное | 7 | 41º12' | 0,659 | аIII=1480 | |
| 4 | ДIV=3080 | ||||
| Марьино | 11 | 28º44' | 0,481 | вIV=1480 | |
| Луговое | 12 | 116º25' | 0,896 | сIV=2760 | |
| Аграрное | 10 | 34º51' | 0,571 | аIV=1760 | |
| Δв=10м | |||||
Из бланка предварительного решения треугольников (таблица 3) выписываем расстояния S (строка 8), находим суммы Q+M и M+Q1, вычисляем значения
k=e p˝ (3) k=e1 p˝ (4) а затем k:s и k1:s.
По формулам:
![]()
![]()
вычислить поправки за центрировку с˝ и редукцию.
Величины М, M+Q,, M+Q1, C" и r" вычислить с точностью: М, М + Q, -до целых минут, с˝ и r˝ до десятых долей угловой секунды.
По результатам полевых измерений (таблица 2), а также на основании рабочей схемы сети (рис. 2) и вычисленных значений поправок за центрировку и редукцию (таблица 4) привести измеренные направления М. На каждом пункте к центру к центрам пунктов (таблица5). Поправки за центровку вводим в измеренные направления на том пункте, на котором были определены элементы центрировок с", Q; поправку за редукцию вводят на пункте наблюдения в измеренные направления на те пункты, на которых были определены элементы редукции.
Таблица 4
Вычисление поправок за центрировку и редукцию
| №№ п.п | п. Пригородное | |||||||||||
|
e=0,025м е1= ─ на пункт Аграрное Q=127º Q1= ─ к=еρ''=5160 к1=е1ρ''= ─ |
||||||||||||
| На пункт обозначения | Аграрное | Луговое | Свобода | |||||||||
|
(10) (6) (5) (7) (9) |
М+QI QI М Q М+Q |
─ ─ 0000' 127 º00' 127 º00' |
─ ─ 41 º12' 127 º00' 168 º12' |
─ ─ 95 º55' 127 º00' 222 º55' |
||||||||
|
(17) (15) (13) (8) (14) (16) |
r'' sin(M+Q') K1:S S K:S Sin(M+Q) |
─ ─ ─ 2250 2,29 0,799 |
─ ─ ─ 1710 3,02 0,204 |
─ ─ ─ 3340 1,54 -0,681 |
||||||||
| (18) | c'' | 1,8 '' | 0,6 '' | -1,0 '' | ||||||||
| №№ п.п | п. Луговое | |||||||||||
|
е=0,030м е1=0,035м на пункт Пригородное Q=181º Q1=36 º к=еρ''=6190 к1=е1ρ''= 7220 |
||||||||||||
|
(10) (6) (5) (7) (9) |
М+QI QI М Q М+Q |
36 º00' 36 º00' 0 º00' 181 º00' 181 º00' |
125 º28' 36 º00' 89 º28' 181 º00' 270 º28' |
241 º53' 36 º00' 205 º53' 181 º00' 386 º53' |
301 º17' 36 º00' 265 º17' 181 º00' 86 º17' |
|
||||||
|
(17) (15) (13) (8) (14) (16) |
r'' sin(M+Q') K1:S S K:S Sin(M+Q) |
2,5'' 0,588 4,22 1710 3,62 -0,017 |
4,0'' 0,814 4,88 1480 4,18 -1,000 |
-3,6'' -0,882 4,13 1750 3,54 0,452 |
-2,3'' -0,855 2,64 2730 2,27 0,999 |
|
||||||
| (18) | c'' | -0,1'' | -4,2'' | 1,6'' | 2,3'' |
|
||||||
| №№ п.п | п. Аграрное | |||||||||||
|
e=0,015м е1= 0,060м на пункт Луговое Q=213º Q1= 293º к=еρ''=3090 к1=е1ρ''= 12380 |
||||||||||||
| На пункт обозначения | Луговое | Пригородное | Марьино | |||||||||
|
(10) (6) (5) (7) (9) |
М+QI QI М Q М+Q |
293 º00' 293 º00' 0 º00' 213 º00' 213 º00' |
342 º21' 293 º00' 49 º21' 213 º00' 262 º21' |
258 º09' 293 º00' 325 º09' 213 º00' 178 º09' |
||||||||
|
(17) (15) (13) (8) (14) (16) |
r'' sin(M+Q') K1:S S K:S Sin(M+Q) |
-7,7'' -0,921 8,36 1480 2,09 -0,545 |
-1,7'' -0,303 5,50 2250 1,37 -0,991 |
-4,4'' -0,979 4,49 2760 1,12 0,032 |
||||||||
| (18) | c'' | -1,1'' | -1,4'' | 0,0'' | ||||||||
| №№ п.п | п. Марьино |
|
||||||||||
|
e= ─ е1= 0,030м на пункт Свобода Q= ─ Q1=238º к=еρ''= ─ к1=е1ρ''= 6190 |
|
|||||||||||
| На пункт обозначения | Пригородное | Аграрное | Свобода |
|
||||||||
|
(10) (6) (5) (7) (9) |
М+QI QI М Q М+Q |
238 º00' 238 º00' 0 º00' ─ ─ |
319 º10' 238 º00' 81 º10' ─ ─ |
347 º53' 238 º00' 109 º53' ─ ─ |
|
|||||||
|
(17) (15) (13) (8) (14) (16) |
r'' sin(M+Q') K1:S S K:S Sin(M+Q) |
-2,2'' -0,848 2,60 2380 ─ ─ |
-2,3'' -0,654 3,54 1750 ─ ─ |
-0,5'' -0,210 2,24 2760 ─ ─ |
|
|||||||
| (18) | c'' | ─ | ─ | ─ |
|
|||||||
| №№ п.п | п. Свобода |
|
||||||||||
|
e= ─ е1= 0,035м на пункт Пригородное Q= ─ Q1=241º к=еρ''= ─ к1=е1ρ''= 7220 |
|
|||||||||||
| На пункт обозначения | Пригородное | Луговое | Марьино |
|
||||||||
|
(10) (6) (5) (7) (9) |
М+QI QI М Q М+Q |
241 º00' 241 º00' 0 º00' ─ ─ |
271 º34' 241 º00' 30 º34' ─ ─ |
310 º59' 241 º00' 69 º59' ─ ─ |
|
|||||||
|
(17) (15) (13) (8) (14) (16) |
r'' sin(M+Q') K1:S S K:S Sin(M+Q) |
-1,9'' -0,875 2,16 3340 ─ ─ |
-2,6'' -1,000 2,64 2730 ─ ─ |
-2,3'' -0,755 3,03 2380 ─ ─ |
|
|||||||
| (18) | c'' | ─ | ─ | ─ |
|
|||||||
Из таблицы 2 выписываем в ведомость вычисления приведенных направлений (таблица 5) названия пунктов и измеренные направления. Сначала записываем и подчеркиваем название пункта, на котором произведены измерения, а под ним названия наблюдаемых с него пунктов
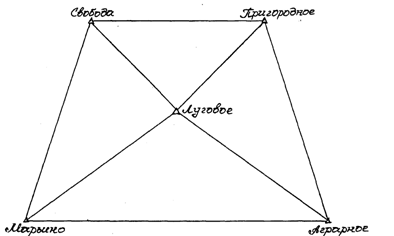
Рис.3. Рабочая схема (углы приведенные)
Таблица 5
Приведение направлений к центрам пунктов
| № №п.п. | Название направлений | Измеренные направления (М) | Поправки за приведения | Приведенныенаправления | ||||
| с | r | (с+r) | (с+r)-(с+r)0 | |||||
| 1 | Аграрное | 0º00'00''49º20'53''325º08'58'' | -1,1''-1,4''0,0'' | 4,0''─-0,5'' | 2,9''-1,4''-0,5'' | 0''-4,3''-3,4'' | 0º00'00''49º20'49''325º08'55'' | |
| Луговое Пригородное Марьино | ||||||||
| 2 | Марьино | 0º00'00''81º10'17''109º53'48'' | ─── | -2,3''-3,6''-4,4'' | -2,3''-3,6''-4,4'' | 0''-1,3''-2,1'' | 0º00'00''81º10'16''109º53'46'' | |
| Свобода Луговое Аграрное | ||||||||
| 3 | Свобода | 0º00'00''30º33'34''69º59'12'' | ─── | ─-2,3''-2,2'' | ─-2,3''-2,2'' | 0''-2,3''-2,2'' | 0º00'00''30º33'32''69º59'10'' | |
| Пригородное Луговое Марьино | ||||||||
| 4 | Луговое | 0º00'00''89º27'38''205º53'02''265º16'56'' | -0,1''-4,2''1,6''2,3'' | ─-7,7''-2,3''-2,6'' | -0,1''-11,9''-0,7''-0,3'' | 0''-11,8''-0,6''-0,2'' | 0º00'00''89º27'26''205º53'01''265º16'56'' | |
| Пригородное Аграрное Марьино Свобода | ||||||||
| 5 | Пригородное | 0º00'00''41º11'30''95º54'38'' | 1,8''0,6''-1,0'' | -1,7''2,5''-1,9'' | 0,1''3,1''-2,9'' | 0''3,0''-3,0'' | 0º00'00''41º11'33''95º54'35'' | |
| Аграрное Луговое Свобода | ||||||||
Вычислить приведенные направления по формуле
M = M +(с + r) + (с + r)0
По данным табл.5 на вторую рабочую схему триангуляции вписать приведенные направления и по ним вычислить приведенные углы.
Вычислить по приведенным углам и выписать в каждом треугольнике сумму углов, невязку W1 и сравнить её с допустимой
![]()
По формуле Ферерро вычислить СКО измеренного угла по невязкам Wi в треугольниках:
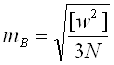 ,
,
где N- число треугольников.
1.2 Уравнивание триангуляции 2-го разряда
1.2.1 Исходные данные
По результатам предварительных вычислений (см. таблицу 5) и исходным данным (см. таблицу 1) выполнить уравнение сети (см. таблицу 3).
Уравнение триангуляции 2-го разряда обычно производят упрощенным коррелатным способом, как более простым для вычислений, но дающим достаточно надежные результаты.
1.2.2 Порядок вычислений
1.2.2.1. В ведомость уравновешивания (таблица 6) со второй рабочей схемы (см. рисунок 3) выписываем углы (графа 3) в том же порядке, как и в предварительном решении треугольников.
1.2.2.2. Составляем условные уравнения и вычисляем первичные поправки: их первые части (i)I' - (за условие фигур) и вторые - (i)I1' (за условие горизонта). Первые части первичных поправок (i)I вычисляем по формуле:
![]() ,
,
где WR- невязка R - го треугольника.
AR , BR , CR - внутренние углы R-треугольника.
Т.е. в каждом треугольнике получают поправку на угол как одну треть невязки за условие фигуры с противоположным знаком.
Таблица 6
Уравновешивание углов и окончательное решение треугольников
| № треуг. | №№ углов | Приведенные углыi | Поправки первичные | Предварительно исправленные углы | Поправкивторичные (i)`` | Уравненныеокончательно углыi`` | Синусы углов I`` | Стороны s(M) | ||
| (i)1| | (i)1| | (i)1 | ||||||||
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 |
| | | 231 | 39º25'38''59 º23'55''81 º10'16'' | +4+3+4 | +2-3+1 | +60+5 | 39 º25'44''59 º23'55''81 º10'21'' | +3─-3 | 39 º25'47''59 º23'55''180 º00'00'' | 0,6351310,8607300,988153 | 2760,771753,452376,282728,06 |
| 179 º59'49''W1=─11 '' | +11 | 0 | +11 | 180 º00'00'' | 0 | 3341,77 | ||||
| || | 564 | 54 º43'02''94 º43'04''30 º33'32'' | +7+8+7 | +2-3+1 | +9+5+8 | 54 º43'11''94 º43'09''30 º33'40'' | +6─-6 | 54 º43'17''94 º43'09''30 º33'34'' | 0,8163530,9966100,508432 | 2728,063330,441699,06 |
| 179 º59'38''W2=─22 '' | +22 | 0 | +22 | 180 º00'00'' | 0 | 2239,43 | ||||
| ||| | 897 | 49 º20'49''89 º27'26''41 º11'33'' | +5+4+3 | +2-3+1 | +7+1+4 | 49 º20'56''89 º27'27''41 º11'37'' | +4─-4 | 49 º21'00''89 º27'27''41 º11'33'' | 0,7587030,9999550,658591 | 1699,062239,331474,87 |
| 179 º59'48''W3=─12 '' | +12 | 0 | +12 | 180 º00'00'' | 0 | 3068,64 | ||||
| IV | 111210 | 28 º43'30''116 º25'35''34 º51'05'' | -3-4-3 | +1-2+1 | -2-6-2 | 28 º43'28''116 º25'29''34 º51'03'' | +7─-7 | 28 º43'35''116 º25'29''34 º50'56'' | 0,4806270,8955200,571414 | 1474,872748,031753,46 |
| 180 º00'10''W4=+10 '' | -10 | 0 | -10 | 180 º00'00'' | 0 | |||||
1.2.2.3. Вычисляем предварительно исправленные углы при центральном пункте «Луговое».
1.2.2.4. Полученные углы выписываем в отдельную таблицу (таблица 7); подсчитываем их сумму и вычисляем невязку W за условие горизонта по формуле:
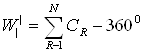 (12)
(12)
где CR - углы при центральном пункте «Луговое».
Для предложенной схемы триангуляции WR|=3|+6|+9|+12|-360˚
Значение WR| не должно превышать величины:
![]() (13)
(13)
где n- число центральных углов CR( число треугольников)
Если WR ≤ WДОП, то вычислить вторые части первичных поправок промежуточных (при центральном пункте) углов по формуле:
(С)'II=─Wr/N (14)
которые с округлением до 1'' записать в таблицу 7 и графу 5 таблицы 6.
1.2.2.5. Чтобы не нарушить ранее выполненных условий фигур, в каждый из связывающих углов треугольника также вводим поправки в размере половины поправки за условие «горизонта» в промежуточный угол при центральной точке, но с противоположным знаком.
Аналогично определяются вторые поправки для остальных треугольников.
Таблица 7
| №№ углов | Центральные углы, исправленные по поправкам (C) | | Поправки (С) ˝ |
|
3 6 9 12 |
59 º23'58'' 94 º43'12'' 89 º27'30'' 116 º25'31'' |
-3'' -3'' -3'' -2'' |
|
360 º00'11'' Wr=11'' |
-11'' |
1.2.2.6. Находим первичные поправки (I)΄ (графа 6. таблица 6), как сумму первых и вторых поправок: (i)΄= (i)΄||+ (i)΄||
1.2.2.7. Вычисляем предварительно исправленные углы, введя в них первичные поправки (i)΄ и записываем их в графу 7.
1.2.2.8. Для определения вторичных поправок (за условие полюса) выписать в таблицу 8 lg первично исправленных углов, при этом в левую часть (графы 1,2) выписывают углы А (1,4,7,10), в правую часть (графы 4,5) - углы В (2,5,8,11).
1.2.2.9. По шестизначным таблицам (или на калькуляторе) выбираем логарифмы синусов углов (бв+ба) при увеличении угла на I".
1.2.2.10. Подсчитываем сумму логарифмов синусов углов в каждой графе ∑1 , ∑2, вычисляем невязку за условие полюса W n =∑1+∑2 и сравниваем ее с допустимой.
Wn =∑1 -∑2 (6-го знака логарифма) ,
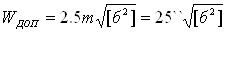 (15)
(15)
где m - средняя квадратическая погрешность измерения угла в сети, [б2] - сумма квадратов приращений синуса угла при увеличении угла на 1˝.
1.2.2.11. Находим для каждого треугольника бА+ бB , (бА+ бB)2 и для всех треугольников ∑(бА+бВ)
1.2.2.12. Определим коррелату k по формуле:
![]() (16)
(16)
1.2.2.13. Вычисляем вторичные поправки в связующие углы каждого треугольника за условие полюса по формуле: (A)˝1=-(B)˝1= k(бА1+бВ2) (17)
Правильность вычисления вторичных поправок контролируем по формуле:
∑ (бА+бВ)A˝ =-Wn (18)
Таблица 8
Вычисление свободного члена полюсного условия и вторичных поправок
| № углов | Lg sin первично направленных углов A| | бА | № углов | Lg sin первично направленных Углов B| | бB | бА+ бB | (бА+ бB)2 | Вторичные поправки | Контроль ∑(бА+бВ)· (A)˝ | |||
| (A)˝ | (B)˝ | |||||||||||
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | ||
|
1 2 3 4 |
0,9948250 0,7062543 0,8186254 0,7569721 3,2766768 |
0,3 3,6 2,4 3,0 |
2 5 8 11 |
0,8028558 0,9118692 0,8800646 0,6817817 3,2765713 |
2,6 1,5 1,8 3,8 |
2,9 5,1 4,2 6,8 |
8,4 26,0 17,6 46,2 98,2 |
3,1 5,5 4,5 7,2 |
3,1 5,5 4,5 7,2 |
-9,0 -28,1 -18,9 -49,0 -105 |
||
Wп=105,5 k=─105,5/92,8=─1,07
1.2.2.14. Выписываем в графу 8 таблицы 6 значения вторичных поправок и вычисляем окончательные (уравновешенные) значения углов (графа 9 таблица 6).
Выполняем контроль вычислений: сумма уравновешенных углов в треугольнике должна быть равна 180°.
1.2.2.15. Выбираем из таблицы (получаем на калькуляторе), значения синусов уравновешенных углов, выписываем их в графу 10 таблица 6 и на основании исходной стороны по теореме синусов (см. предварительное решение треугольников) вычисляем все стороны треугольников системы.
Контролем является то, что вычисленное значение исходной стороны должно отличатся от ее заданного не более, чем на 3 см.
1.2.2.16. На схеме (рисунок 1) наметить: «ходовую» линию через определяемые пункты «Луговое», «Свобода», «Пригородное», «Аграрное». Выписать в таблицу 9: а) графы 3, 4, 5, б, 7, 8 - названия определяемых пунктов, б) графу 3 - исходные данные αисх , x1 , y1 ; в) в графы 4, 5, 6, 7 - углы поворота β или λ, и длины сторон S (по данным таблицы 6).
1.2.2.18. По известным формулам:
ai =ai-1+180˚-βi (19), ai =ai-1-180˚+λi (20)
определяем дирекционные углы «ходовой» линии по дирекционному углу исходной линия αисх и углом поворота βi или λi Контролем вычислений ai будет являться aисх (графа 8, таблица 9). Переходим от дирекционных углов к румбам.
1.2.2.19. Вычисляем для каждой ходовой линии приращения координат по известным формулам: Δxi=dicosri (19), Δyi=disinri (20).
При вычислениях функции синусов и косинусов брать до 6-го знака после запятой. Приращения координат округлить до 2-го знака.
1.2.2.20. Определяем последовательно координаты определяемых пунктов по формулам:
x2=x1+∆x1-2
и
y2=y1+∆y1-2 (22)
где x 1 ,y1 и x2,y2 координаты соответственно исходного и определяемого пунктов.
Контролем вычислений координат будет: координаты исходного пункта «Марьино», полученные в результате вычислений (графа б, таблица 9), не должны отличатся от них заданного значения (графа 3) более 3 см.
Таблица 9
Вычисление координат пунктов сети.
| Порядок действий | Обозначения | Названия пунктов: 1 исходных ; 2 определяемых | |||||
| Марьино Луговое | Луговое Свобода | СвободаПригородное | ПригородноеАграрное | Аграрное Марьино | Марьино Луговое | ||
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| I | αисх | 72 º28'50'' | 72 º28'50'' | 311 º52'45'' | 101 º19'11'' | 185 º24'21'' | 281 º12'25'' |
| 5 | β | ─ | 59 º23'55'' | 30 º33'34'' | 95 º54'50''59 º23'58''59 º23'58'' | 84 º11'56'' | 28 º43'35'' |
| 6 | Α1-2 | 72 º28'50'' | 311 º52'45'' | 101 º19'11'' | 185 º24'21'' | 281 º12'25'' | 72 º28'50'' |
| 7 | R1-2xx | 72 º28'50'' | 48 º07'15'' | 78 º40'49'' | 5 º24'21'' | 78 º47'35'' | |
| 12 | X2 | 5536,34 | 7357,49 | 6703,78 | 4474,41 | 5008,50 | 5008,50 |
| 2 | X1 | 5008,50 | 5536,34 | 7357,49 | 6703,78 | 4474,41 | |
| 11 | ∆x1-2 | 527,84 | 1821,15 | -653,71 | -2229,37 | 534,09 | |
| 8 | Cos r1-2S | 0,301029 | 0,667562 | 0,196284 | 0,995552 | 0,194353 | |
| 4 | S1-2sin | 1753,45 | 2728,06 | 3330,44 | 2239,33 | 2748,030,980932 | 1753,45 |
| 19 | Sin r1-2 | 0,953615 | 0,744554 | 0,980547 | 0,094210 | 0,980932 | |
| 10 | ∆y1-2yY1 | 1672,12 | -2031,19 | 3265,65 | -210,97 | -2695,63 | |
| 3 | Y1 | 1000,00 | 2672,12 | 640,93 | 3906,58 | 3695,61 | 999,98 |
| 13 | Y2 | 2672,12 | 640,93 | 3906,58 | 3695,61 | 999,98 | |
1.2.2.21. Выписываем координаты исходных пунктов из таблицы 9 в каталог координат (таблица 10), а также дирекционные углы направлений на один или два смежных пункта и расстояния до них. В камлоте координат дается также характеристика типа знака, центра и указывается класс исполненной ости.
Как ответственный документ каталог заполняется, считается и подписывается двумя исполнителями.
Таблица 10
Каталог координат пунктов триангуляции 2 разряда (местная система координат).
| № № п. п. | Название пункта тип и высота знака тип центра | Разряд | Координаты Х , м У, м | Длина сторон | Дирекционные углы | На пункт |
| 1 |
Свобода пир.6,2м центр 2 типа |
2 |
7357,49 640,93 |
3330,44 2728,06 2376,28 |
101 º19'11'' 131 º52'45'' 171 º18'32'' |
Пригородное Луговое Марьино |
| 2 |
Пригородное пир.6,8м центр 2 типа |
2 |
6703,78 3906,32 |
2239,33 1699,06 3330,44 |
185 º24'21'' 226 º35'54'' 281 º12'25'' |
Аграрное Луговое Свобода |
| 3 |
Аграрное пвр,6,5м центр 2 типа |
2 |
4474,41 3695,61 |
2239,33 2748,03 |
5 º24'21'' 281 º12'25'' |
Пригородное Марьино |
| 4 |
Луговое пир.6,3м центр 2 типа |
2 |
5536,34 2672,12 |
1753,45 2728,06 |
252 º28'50'' 311 º52'45'' |
Марьино Свобода |
| 5 |
Марьино пир 6,6м центр 2 типа |
1 |
5008,50 1000,00 |
1753,45 2748,03 2376,28 |
72 º28'50'' 101 º12'25'' 351 º18'32'' |
Луговое Аграрное Свобода |
2. Уравновешивание систем ходов плановой съемочной сети
2.1 Уравновешивание систем теодолитных ходов с одной узловой точкой
2.1.1 Задание
Произвести уравновешивание систем теодолитных ходов, сходящихся в узловой точке 3 и опирающихся на линии геодезической сети АВ, СD, ЕF с известными дирекционными углами на пункты В, D и F с известными координатами.
Схема ходов и значения измеренных углов и длин линий приведены на рисунке 5.
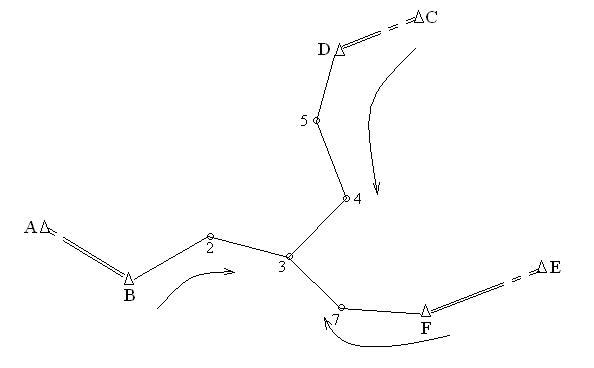
Рис.5 Схема ходов
Таблица 11
Исходные данные.
| № №варианта | Координаты пунктов | Дирекционные углы | |||||||
| В | D | F | αAB | αCD | αEF | ||||
| Х | У | Х | У | X | Y | ||||
| 8 | 2434,45 | 4508,48 | 2148,82 | 3282,66 | 3436,02 | 4074,02 | 304° 15,4' | 52° 38,7' | 108° 44,1' |
Вычисления всех дирекционных углов выполнить с округлением до 0,1'. Приращение координат и координаты вычислить с округлением до 0,01м.
В результате уравнивания сети ходов должны быть представлены:
1. Схематический чертеж (рис. 5)
2. Ведомость вычисления координат (таблица 12).
3. Таблица вычислений окончательных значений дирекционного угла узловой линии (таблица 13).
4. Таблица вычислений окончательных значений координат узловой точки (таблица 14).
2.1.2 Порядок решения
2.1.2.1. По схеме намечаем узловую линию, например линию 2-3. Выписываем в ведомость координат (таблица 12) измеренные углы (графа 2) и дирекционные углы твердых линий (графа 4). Подсчитываем суммы измеренных углов по каждому из ходов.
2.1.2.2. По всем трем ходам вычисляем дирекционный угол узловой линии и результаты записываем в графу 2 таблицы 13, а в графу 4 записываем число углов по каждому ходу.
2.1.2.3. Оцениваем качество угловых измерений, составив для этого разности вычисленных для узловой линии дирекционных углов. Первую разность составляем из дирекционных углов, найденных по двум ходам с наименьшим числом углов. Полученная разность равна угловой невязке этих двух ходов. Сравнить эту разность с допустимой невязкой определяемой по формуле:
![]() (23)
(23)
где ![]() - число углов в обоих ходах.
- число углов в обоих ходах.
Другую разность составляем из дирекционных углов, вычисленных по третьему ходу и одному из двух первых. Эту невязку также сравнивают с предельной, определяемой по формуле (23). Результаты вычислений записываем в графу 9 таблицы 13.
Таблица 12
Ведомость вычисления координат.
| № точек | Углы | Горизонтальное проложение | Приращения координат | Координаты | ||||||
| измер. | исправл. | дирекц. | вычисленные | исправленные | ||||||
| ∆x | ∆y | ∆х | ∆y | х | y | |||||
| 1 | 2 | 3 , | 4 | 5 | б | 7 | 8 | 9 | 10 | 11 |
| A | (левые) | 304° 15,4' | 1-й ход | |||||||
| B | 155°17.5' | 155° 17.5' | 279°32.9' | 200,42 | -233,25 | -4-197,64 | +33,23 | -197,68 | 2434,45 | 4508,48 |
| 2 | -0.1'223°43.0' | 223° 42.9' | 323°15,8' | 322,34 | -2258,32 | -5+192,80 | 258,30 | -192,85 | 2467,68 | 4310,80 |
| 3 | 2725,98 | 4117,95 | ||||||||
![]() 379°00,5’ P= 522,76
379°00,5’ P= 522,76 ![]() 291,57
291,57 ![]() -390,44
-390,44
![]() 379°00,4’
379°00,4’ ![]() 291,53
291,53 ![]() 390,53
390,53
![]() +0,1’ fх=0,04 fу=0,09
+0,1’ fх=0,04 fу=0,09
![]() 1.4’ fабс=0,01 fотн=0,01/523=1/52300
1.4’ fабс=0,01 fотн=0,01/523=1/52300
| 1 | 2 | 3 | 4 | 5 | б | 7 | 8 | 9 | 10 | 11 |
| C | (правые) | 52°38,7' | ||||||||
| D | -0.2'187°20,5' | 187° 20.3' | 45°18.4' | 439.44 | +4309.06 | -3312,39 | +309,10 | 312,36 | 2148,82 | 3282,66 |
| 5 | -0.1'187° 35,5' | 187° 35,4' | 37°43,0' | 292.83 | +5231,64 | -3179,14 | +231,69 | 179,11 | 2457,92 | 3595,02 |
| 4 | -02'133° 45,0' | 133° 44.8' | 83°58.2' | 345.76 | +536.32 | -3343,85 | 36,37 | 343,82 | 2689,61 | 3774,13 |
| 3 | -0.1'120° 42,5' | 120° 42.4' | 143°15.8' | 2725,98 | 4117,95 |
![]() 629°23.5' P=1078.03
629°23.5' P=1078.03 ![]() 577,02
577,02 ![]() 835,38
835,38
![]() 629°22.9'
629°22.9' ![]() 577,16
577,16 ![]() 835,29
835,29
![]()
![]() +0.6' fх= -0,14 fу=0,09
+0.6' fх= -0,14 fу=0,09
![]() 2,0' fабс=0,17 fотн=0,17/1078= 1/6000
2,0' fабс=0,17 fотн=0,17/1078= 1/6000
| 1 | 2 | 3 | 4 | 5 | б | 7 | 8 | 9 | 10 | 11 |
| E | (правые) | 108°44.1' | ||||||||
| F | +0,1'153°20.5' | 153°20.6 | 135°23,5' | 335.45 | -2-238,81 | +12235,57 | -238,83 | 235,69 | 3436,02 | 4074,02 |
| 7 | +0,1'113°14.0 | 113°14.1 | 202°09.4' | 508.76 | -2-471,19 | +11-191,87 | -471,21 | -191,76 | 3197,19 | 4309,71 |
| 3 | +0,1'238°53.5 | 238°53.6 | 143°15.8' | 2725,98 | 4117,95 |
![]() 505°28,0' P=844,21
505°28,0' P=844,21 ![]() -710,00
-710,00 ![]() 43,70
43,70
![]() 505°28,3'
505°28,3' ![]() -710,04
-710,04 ![]() 43,93
43,93
![]()
![]() - 0,3' fх= +0,4 fу= -0,23
- 0,3' fх= +0,4 fу= -0,23
![]() 1,6' fабс=0,23 fотн=0,23/844= 1/3700
1,6' fабс=0,23 fотн=0,23/844= 1/3700
2.1.2.4. Определяем веса вычисленных значений дирекционного угла узловой линии по формуле:
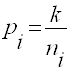
где ni - число углов в i - м ходе,
k - произвольный коэффициент, выбираемый так, чтобы веса выражались числами близкими к единице. Найденные веса записываем в графу 5 таблицу 13 с округлением до 0,01.
Таблица 13
Вычисление окончательного значения α2-3
| № ходов | Дирекционные углы | εi | Числоуглов |
|
PE | Невязкиfβ | pfβ | проверкадопустимостиугловых.невязок |
| 1 | 2 | 3 | 4 | 5 | б | 7 | 8 | 9 |
| 1 | 143°15.9' | +0.7 | 2 | 6 | 4.2 | -0.1 | +0.6 | fβ1-3=α3-α1=+0,2'fβдоп=1'√(n1+n3)=1'√5≈2.2'fβ2-3=α3-α2=+0,9'fβдоп=1'√(n2+n3)=1'√5≈2.6' |
| 2 | 143°15.2' | 0 | 4 | 3 | 0 | +0.6 | -1.8 | |
| 3 | 143°16.1' | +0.9 | 3 | 4 | 3.6 | -0.3 | +1.2 |
a0= 143°15.2’ [PE]=+7.8 [P]=13 [Pfβ]=0
а=143°15,8'
Контроль: ω[P]= 0
2.1.2.5. По формулам общей арифметической средины:
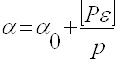
где α0- приближенное значение искомого дирекционного
угла, ε1 - остаток, определяемый по формуле: ![]() (i=1,2,3) (26), вычислить
окончательное значение дирекционного угла α.
(i=1,2,3) (26), вычислить
окончательное значение дирекционного угла α.
2.1.2.6. Вычисляем угловые невязки ходом для правых углов по формуле:
![]() (27),
(27),
для левых углов по формуле:
![]() (28)
(28)
Полученные значения невязок записать в графу 7 таблицы 13. Выполнить контроль вычисления невязок по формуле: [pfβ] =0
Вследствие ошибок округлений это равенство может не выполняться.
В этом случае [pfβ]=ω[P] (30), ![]() где ω- ошибка
округления при делении [ Pε ] на [ p ].
где ω- ошибка
округления при делении [ Pε ] на [ p ].
2.1.2.7. Полученное окончательное значение дирекционного угла α узловой линии в дальнейшем принимают за твердое и записывают в графу 4 таблицы 12. Затем вычисляют теоретические суммы углов по каждому ходу по формулам:
• для правых углов
![]()
• для левых углов
![]()
где αн и αк - начальный и конечный углы хода, найти угловые невязки и сличить их с полученными в графе 7 таблица 12, учитывая, что невязки для правых и левых углов одного и того же хода противоположны по знаку (ход 1).
Если полученные невязки меньше предельных, то распределим их с противоположным знаком поровну на углы соответствующих ходов (с округлением до 0,1').
2.1.2.8.Вычисляем дирекционные углы по формулам:
• для правых углов: α1=αi-1+180˚-βi (33)
• для левых углов: α1=αi-1+180˚-λi
Таблица 14
Вычисление окончательных значений координат узловой точки 3.
| №№хода | X,м | εx`см | Pεx`см | fx`см | Pfx`см | Sкм |
k=4 |
Pfy`см | fy`см | Pεy`см | εx`см | Y,м |
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 |
| 1 | 2726,02 | 0,18 | 1,44 | +0.04 | +0.32 | 0.5 | 8 | +0.72 | +0.07 | +2,56 | +0,32 | 4118,04 |
| 2 | 2725,84 | 0,18 | 0 | -0.14 | -0.56 | 1.0 | 4 | 0 | 0,36 | +1,28 | +0,32 | 4118,04 |
| 3 | 2726,02 | +0.2 | +0,9 | +0.04 | +0.20 | 0.8 | 5 | -0.6 | -0,23 | 0 | 0 | 4117,72 |
X0 = 2725,84 [pεx]= 2.34 [pfx]= -0,04 [p]= 17
y0=4402.09 [pfy]= +0,07 [pεy]= -3,84
X= 2725,98 y=4117,95
Контроль: ωx[p]=0,06 ωy[p]= 0,05
2.1.2.9. Вычисляем приращения координат и их суммы (см. таблицу 12), а затем - координаты узловой точки по всем трем хода. Результаты вычислений записать в графы 2 и 13 таблицы 14.
Проверка допустимости линейных невязок
| №№ ходов | Si+j м | Fx=xi-xj | Fy=yi-yj | fабс | Fотн м |
| 1 | 2 | 3 | 4 | 5 | 6 |
| 1+2 | 1600 | +0.18 | 0 | +0.18 | 1:8900 |
| 2+3 | 1923 | -0.18 | +0.32 | +0.37 | 1:5200 |
2.1.2.10. Оцениваем качество измерений, вычислив для этого невязки по ходам: по первому - вместе со вторым и по второму - вместе с третьим.
Для этого составляем разности координат по соответствующим парам ходов:
Fx=xi-xj
Fy=yi-yj (34)
Одна пара ходов берется с наименьшими периметрами. Подсчеты невязок выписываем внизу таблицы 14.
Относительные невязки не должны превышать 1:1000.
2.1.2.11. Вычисляем веса значений координат узловой точки
по формуле:![]()
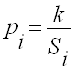
в которой
Si - длина соответствующего хода, выражаем в километрах;
k — произвольный коэффициент, выбираем с таким же расчетом, как и при вычислении дирекционных углов. Результаты вычислений записываем в графу 8 таблица 14.
2.1.2.12. По формуле общей арифметической средины:

где x0 , y0 - приближенные значения координат Х и У,
εxi ,εyi - величины определенные по формулам:
εxi=xi-x0
εyi=yi- y0 (37)
Вычисляем окончательные значения координат узловой точки Х и У. Полученные значение записываем в таблицу 12.
2.1.2.13. Вычисляем невязки приращений координат для каждого хода по формулам:
fx=xi-x0
fy=yi-y0 (33)
и записываем их в графы 5 и 10 таблицу 14.
Выполняем контроль вычисления Х и У и невязок по формулам:
[pfx]=-ωx[p] (39) , [pfy]=-ωy[p] (40)
где ωx и ωy - ошибка округлений при делении [pεx] и [pεy] на [p].
2.1.2.14. Вычисляем для каждого хода в ведомости координат (таблица 12) вторично невязки по формулам:
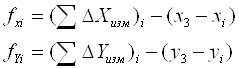
где ![]() и
и ![]() - измеренные суммы приращений
координат по каждому ходу;
- измеренные суммы приращений
координат по каждому ходу;
Xi и Yi - координаты начальной точки соответствующего хода;
X3 и Y3 - координаты узловой точки (точка 3).
Эти невязки сличают с полученными ранее.
Данные подсчитываем по каждому ходу fабс и fотн. Если последнее не превышают 1:1000, то невязки в приращениях координат распределяем на соответствующие приращения с противоположными знаками, пропорционально длине линий.
Затем в графах 8 и 9 таблица 12 вычисляем исправленные приращения координат.
2.1.2.15. По исправленным приращениям координат вычисляем координаты всех точек (графы 10 и 11 таблица 12).
2.2 Уравновешивание углов сети теодолитных ходов по способу полигонов профессора В.В.Попова
2.2.1 Задание
Уравновесить углы и вычислить дирекционные углы сторон сети, изображенной на рисунке 6.
Исходные данные.
| №№ варианта | Дирекционные углы | |
| αАВ | αСD | |
| 24 | 353°08,2' | 35°20,1' |
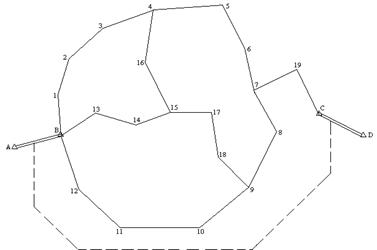
Рис.6 Схема полигонов
2.2.2 Порядок решения
2.2.2.1. Подсчитываем число полигонов, включая и несомкнутый полигон между твердыми (исходными) сторонами АВ и CD.
2.2.2.2. Исправить непосредственно на схеме полигонов (рисунок 6) сумму углов при каждой внутренней узловой точке (15 и 9) для соблюдения условий горизонта (360°), внеся поправки поровну на каждый угол до десяти долей минуты. Поправки записываем на схеме у соответствующих углов в десятых долях минуты. Например, поправку +0,1' записываем в виде +1.
2.2.2.3. Подсчитываем сумму измеренных углов в каждом полигоне с учетом поправок за условие горизонта и записываем ее на схеме внутри соответствующего полигона (см. рисунок 6). Несомкнутый полигон IV, включающий твердые линии АВ и CD условно считаем сомкнутыми при помощи пунктирной линии. Число углов, сторон или направлений по этой пунктирной линии в процессе вычислений считается равным нулю.
Под практической суммой углов в каждом полигоне записываем сумму углов теоретическую, причем по полигону IV теоретическую сумму углов следует вычислять по формуле:
![]()
Вычисляем для каждого полигона полученную невязку в сумме углов
![]()
и сравниваем ее с предельной,
![]()
где n- число углов полигона.
Полученные предельные невязки записываем на схеме (см. рис. 6) под соответствующими суммами углов в каждом полигоне.
2.2.2.4. Составляем схему сети теодолитных ходов для уравновешивания углов (рисунок 7). На этой схеме выписываем номера узловых точек и полигонов. Внутри каждого полигона под его номером заготовить табличку невязок и около каждого звена, кроме пунктирного, таблички поправок. В таблички записываем полученные невязки.
2.2.2.5. Вычисляем красные числа для каждого звена всех полигонов по правилу: красное число звена равно числу направлений в звене, деленному на число направлений в полигоне.
При этом каждую линию в замкнутых полигонах |,||, и ||| а в полигоне IV твердые линии АВ и СD считаем каждую за одно направление. Поэтому на чертеже пунктирная линия, условно замыкающая полигон, вычерчивается у середины твердых линий, включая в полигоне не целые линии, а одно направление.
Контроль: сумма красных чисел по каждого полигону должна быть точно равна единице. Красные числа выписать красным цветом под соответствующими табличками.
2.2.2.6.Распределяем невязки пропорционально красным числам соответствующих полигонов. Начинаем с полигона, имеющего наибольшую по абсолютной величине невязку, умножая, ее последовательно на красные числа звеньев данного полигона и вносим произведения в соответствующие таблички поправок со знаком невязки, с округлением до 0.1΄
2.2.2.7. Подсчитываем алгебраические суммы чисел, а таблицу поправок и записываем их над двойной чертой.
Подсчитываем поправки во внутренние углы каждого полигона по всем звеньям. Для внутренних звеньев сети поправки получаем так: изменяем знак суммы чисел внешней по отношению к полигону таблички и складываем с суммой чисел внутренней таблички того же знака. Для каждого внешнего звена сети поправка равна итогу внешней таблички с противоположным знаком. Все поправки на звенья записываем в скобках внутри полигона у соответствующих звеньев (см. рис. 7).
Контроль вычислений поправок: их сумма по каждому полигону должна быть равна невязке полигона с обратным знаком.
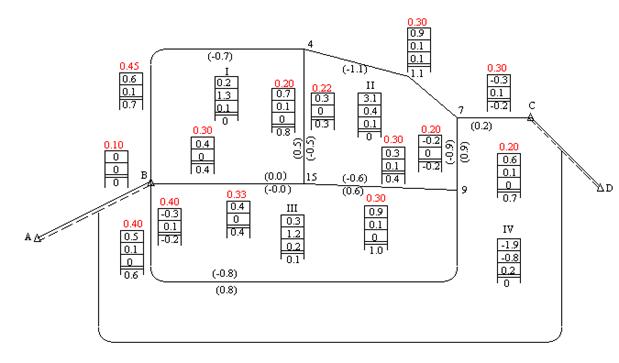
Рис.7 Схема уравновешивания
![]() 1757°49,8'
1757°49,8' ![]() 1032°35,1'
1032°35,1'
![]() 1757°48,1'
1757°48,1' ![]() 1032°33,1'
1032°33,1'
![]() +1,7'
+1,7' ![]() +2,0'
+2,0'
![]() 3,3'
3,3' ![]() 2,6'
2,6'
![]() 1030°24,5'
1030°24,5' ![]() 407°25,6'
407°25,6'
![]() 1030°25,1'
1030°25,1' ![]() 407°26,0'
407°26,0'
![]() -0,6'
-0,6' ![]() -0,4'
-0,4'
![]() 2,6'
2,6' ![]() 1,7'
1,7'
2.2.2.8. Распределение поправки звеньев на каждый угол.
Для этого поправку, приходящуюся на звено, делим на число направлений и полученную поправку направления вводим в углы при узловых точках, а в остальные углы – удвоенную поправку. Следовательно, каждый угол при узловой точке должен получить по две поправки, приходящиеся на этот угол от каждого направления обоих звеньев.
Поправки углов записываем под (или над) соответствующими углами непосредственно на схеме (рис.6). При узловых точках поправки от каждого звена записываем отдельно.
2.2.2.9. Выписываем в ведомость вычисления дирекционных углов со схематического чертежа измеренные углы и на нем соответствующие поправки. Подсчитываем допустимую невязку и сравниваем с ней полученную. Контроль: сумма поправок должна быть равна полученной невязке с противоположным знаком. Выписываем исправленные углы, подсчитываем для контроля их суммы и вычисляем дирекционные углы сторон всех ходов.
2.3 Уравновешивание системы полигонометрических ходов способом последовательных приближений
2.3.1 Задание
По данным, указанным на схеме полигонометрических ходов (рис. 8, 9), способом последовательных приближений произвести уравновешивание:
• дирекционных углов узловой линий;
• координат узловых точек.
В таблице 17 приведены по вариантам углы при точках № 1,12,16. Остальные углы принять такими же, как и на схеме (см. рис. 8).
Таблица 17
Значения углов № 1,12,16.
| №№ варианта | Углы | |||
| 1 | 12 | 16 | ||
| 24 | 140°00’48’’ | 125°34’36’’ | 150°06’51’’ | |
Таблица 18
Суммы приращений координат по звеньям.
| №№ варианта | Суммы приращений координат | |||||
| Звено 1 | Звено 2 | Звено 3 | Звено 4 | Звено 5 | Звено 6 | |
| 24 |
+670,50 +954,10 |
+472,45 +2972,97 |
+595,90 +872,40 |
-1475,65 +253,55 |
-2568,70 -4242,67 |
+1002,95 -3225,53 |
2.3.2.2 Порядок уравновешивания.
2.3.2.1.Вычисление дирекционных углов.
2.3.2.1.1. На схематическом чертеже (см. рис. 8) у каждого звена выписываем в виде дроби: в числителе номер звена и сумму измеренных углов, в знаменателе - число углов (звеном называют часть хода, заключенного между угловыми линиями или между «твердой» и узловой линией).
![]() 2.3.2.1.2.
По данным, представленным на чертеже, подсчитываем угловые невязки по ходам и
замкнутому полигону и выписываем их на чертеж (см. рис. 8). Если угловые невязки
не превышают допустимой, то продолжаем вычисление.
2.3.2.1.2.
По данным, представленным на чертеже, подсчитываем угловые невязки по ходам и
замкнутому полигону и выписываем их на чертеж (см. рис. 8). Если угловые невязки
не превышают допустимой, то продолжаем вычисление.
2.3.2.1.2. Заполняем ведомость вычисления дирекционных углов (таблица 19) в следующем порядке:
• выписываем исходные данные дирекционные углы «твердых» линий с чертежа сети;
• в графу 1 выписываем название узловых линий, для которых вычисляются дирекционные углы;
• в графу 2 выписываем наименование начальных (исходных) линий (твердых и узловых) звена, от которых можно вычислить искомые дирекционные углы, при этом в первую очередь выписываем наименование «твердых», исходных сторон;
• в графу 3 выписываем номера звеньев примыкающих к соответствующей узловой (искомой) линии, графы 4, 5 и 6 заполняем со схемы ходов в соответствии с их названием;
• вычисляем веса дирекционных углов по каждому звену (до 0,01) по формуле:
где i = 1,2,3,... „- номер звена; k - произвольный постоянный коэффициент обычно выбираем так, чтобы веса выражались числами близкими к единице;
ni - число углов звена.
Для дирекционного угла каждой узловой линии вычисляем сумму весов примыкающих к ней звеньев и определяем веса по формуле:
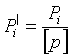
Контроль:[P΄]=1
• вычисляем методом последовательных приближений значения дирекционных углов узловых линий.
Нулевое приближение для дирекционных углов каждой узловой линии вычисляем непосредственно от « твердой» стороны:
![]() (48)
(48)
![]() (49)
(49)
Нулевое приближение записываем в первых строках каждого блока графы 9 и подчеркиваем;
![]() • для
вычисления первого приближения дирекционного угла каждой узловой линии находим
значения дирекционного угла этой линии путем передачи от исходных данных по
воем примыкающим к ней звеньям. Из полученных значений найти среднее весовое
значение (графы 9,10)
• для
вычисления первого приближения дирекционного угла каждой узловой линии находим
значения дирекционного угла этой линии путем передачи от исходных данных по
воем примыкающим к ней звеньям. Из полученных значений найти среднее весовое
значение (графы 9,10)
где α0 - приближенное (наименьшее) значение дирекционного угла узловой линии (взятое до целых минут) из полученных значений по каждому примыкающему звену:
![]()
Это и будет первым приближением.
Аналогично вычисляем второе, а затем и следующие приближения (графы 11,...). При вычислении каждого последующего приближения за исходные данные принимаем самые последние значения приближений.
Приближения заканчиваем тогда, когда последнее вычисленное приближение дает одинаковый результат с предыдущим. Это последнее приближение и является окончательным значением о. Величины εi и α вычисляем до целых секунд;
• для контроля вычислений определяем поправки в углы по звеньям.
![]() (углы
левые), (52)
(углы
левые), (52)
где α и αi - значения дирекционных углов соответственно узловой линии, записанные в графы последнего приближения, и окончательное.
![]() Выполнение
равенства: (53)
Выполнение
равенства: (53)
служит контролем правильности вычисления окончательного значения дирекционного угла.
![]() Из-за
погрешностей округления Σ P`iνi может быть не равно нулю, но должна
быть
Из-за
погрешностей округления Σ P`iνi может быть не равно нулю, но должна
быть
![]() Значения
поправок νi выписать на схему ходов (см. рис. 8) красным цветом над суммой
измеренных углов соответствующего звена и произвести подсчет поправок по ходам,
имея в виду, что т.е. в случае правых углов знак полученной поправки должен
быть изменен на противоположный.
Значения
поправок νi выписать на схему ходов (см. рис. 8) красным цветом над суммой
измеренных углов соответствующего звена и произвести подсчет поправок по ходам,
имея в виду, что т.е. в случае правых углов знак полученной поправки должен
быть изменен на противоположный.
Контроль: сумма поправок по ходу должна быть равна невязке с обратным знаком.
Таблица 19
Вычисление дирекционных углов узловых точек.
| № линии | № звена | Суммауглов взвене | Число углов | Углы β и λ | Веса | Приближенияиближалн | |||||||||||||||||
| Искомой | Исходной | P | P` |
|
P`ε | || | P`ε | ||| | P`ε | IV | P`ε | V | P`ε | VI | P`ε | VII | P`ε | νλ | P`νλ | ||||
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 | 21 | 22 | 23 | 24 |
| 2-15 |
АВ 11-14 16-7 |
1 6 2 |
500°07'30'' 280°12'52'' 854°49'04'' |
3 2 6 |
П П Л |
2 3 1 |
0,33 0,50 0,17 |
190°02'54'' 1'18'' 1'46'' |
0 12 9 |
54 0 25 |
0 3 5 |
54 6 36 |
0 6 7 |
54 2 34 |
0 4 7 |
54 4 35 |
0 5 7 |
54 3 35 |
0 5 7 |
12 3 -29 |
3,96 1,5 -4,93 |
||
| 6,0 | 1,00 | 1'15'' | 21 | 2 | 8 | 7 | 13 | 5 | 11 | 6 | 12 | 6 | 12 | 0,53 | |||||||||
| 11-14 |
EF 2-15 16-7 |
5 6 4 |
328°51'38'' 280°12'52'' 664°58'32'' |
3 2 5 |
Л Л П |
2 3 1,2 |
0,32 0,48 0,20 |
290°15'50'' 46'' 1'10'' |
1 0 5 |
50 7 49 |
0 9 0 |
50 54 00 |
0 2 2 |
50 59 58 |
0 4 2 |
50 57 59 |
0 3 2 |
50 58 59 |
0 4 2 |
50 58 59 |
0 4 2 |
6 -2 -3 |
1,92 -0,96 -0,6 |
| 6,2 | 1,00 | 52'' | 6 | 58 | 9 | 54 | 4 | 56 | 6 | 55 | 5 | 56 | 6 | 56 | 6 | 0,36 | |||||||
| 16-7 |
DС 15-2 14-11 |
3 2 4 |
475°06'18'' 854°49'04'' 664°58'32'' |
2 6 5 |
Л П Л |
3 1 1,2 |
0,58 0,19 0,23 |
55°14'42'' 13'50'' 13'54'' |
30 0 1 |
42 11 24 |
18 0 3 |
42 58 26 |
26 0 6 |
42 3 26 |
23 0 5 |
42 1 28 |
24 0 6 |
-11 30 3 |
-6,38 5,7 0,69 |
||||
| 5,2 | 1,00 | 14''21'' | 31 | 21 | 21 | 30 | 32 | 31 | 28 | 31 | 30 | 0,01 | |||||||||||
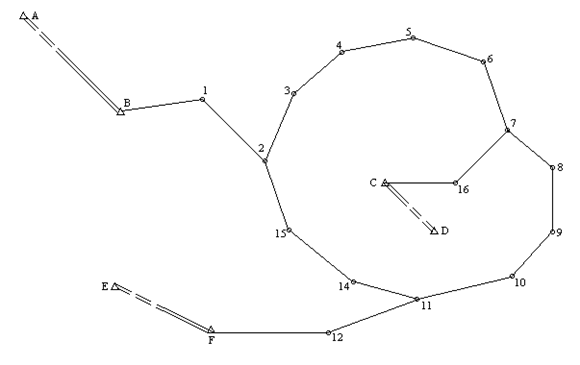
Рис.8 Схема для вычисления дирекционных углов опорных линий
2.3.2.2. Вычисление координат.
2.3.2.2.1. По данным, указанным на чертеже (рис. 9), подсчитываем линейные невязки по ходам и по замкнутому полигону и выписываем их на чертеже.
Если fотн ≤1/5000 (56), то производим дальнейшие вычисления.
2.3.2.2.2. По имеющимся на чертеже данным заполнить ведомость вычисления координат (табл.20).
а) выписываем исходные координаты «твердых» пунктов;
б) выписываем названия искомых узловых и исходных точек в том же порядке, как и при вычислении дирекционных углов;
в) выписываем номера звеньев, примыкающих к исходной узловой точке;
г) выписываем суммы приращений ∑Δхпр и ∑Δупр и периметры ∑di для каждого звена;
д) вычисляем веса сумм приращений координат по каждому звену по формулам:
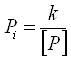

![]()
Контроль:е) вычисляем нулевые приближения координат узловых точек путем передачи координат по одному звену от твердых точек:
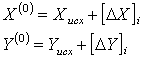
и записываем в первых строках каждого блока графы 8 таблицы 20.
ж) аналогично вычисляем, дирекционных углов получаем первые, вторые и т.д. приближения координат узловых точек по формулам:
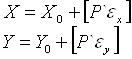
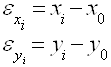
где X0 и Y0 - приближенные значения координат узловой точки, взятые до целого центра;
X , Y- значения координат узловой точки полученные по каждому звену. Значения pi , εx и εy, вычислить в сантиметрах с округлением до 1 см;
з) для контроля вычислений определяем поправки νx1 и νy1 в суммах приращений по ходам. Эти поправки равны разностям между окончательными значениями координат и значениями, записанными в той же графе, которые получены по отдельным звеньям.
![]() Контролем
правильности вычислении среднего весового приращения координат для каждой
узловой точки служит равенство: (62)
Контролем
правильности вычислении среднего весового приращения координат для каждой
узловой точки служит равенство: (62)
![]() Вследствие
погрешностей округлений равенство (62) точно не выполняется, но должно быть
(63)
Вследствие
погрешностей округлений равенство (62) точно не выполняется, но должно быть
(63)
Поправки в приращениях записываем в графу 14 таблицы 20, а так же выписываем красным цветом на схеме (см. рисунок 9) над соответствующими суммами приращений. Следует иметь ввиду, что знак поправок соответствует приращению хода, указанному стрелкой.
Контроль: сумма поправок по отдельным ходам равна невязке с обратным знаком.
Вычисление ординат узловых точек
Ув=25763,05м Ус=28817,35м УF=25700,48м
Таблица 20
Вычисление абцисс узловых точек
Хв=31361,65м Хс=31908,90м ХF=28461,05м
| пункты | № звена | Суммаприращенийвзвене | Длина звена, км | Веса | Приближенияиближалн | |||||||||||||||
| Искомый | Исходный | P | P` |
|
P`ε | || | P`ε | ||| | P`ε | IV | P`ε | V | P`ε | VI | P`ε | νλ | P`νλ | |||
| 1 | 2 | 3 | 4 | 56 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 | 21 |
| 2 |
В 7 11 |
1 2 6 |
670,50 -472,45 1002,95 |
1,1 4,0 5,3 |
3,64 1,00 0,75 |
0,68 0,18 0,14 |
32032, 15 35 90 |
0 4 11 |
15 45 1,34 |
0 5 17 |
15 36 49 |
0 4 5 |
15 42 48 |
0 5 5 |
15 39 46 |
0 4 4 |
15 39 45 |
0 4 4 |
8 -16 -22 |
5,44 -2,88 -3,08 |
| 5,39 | 1,00 | 30 | 15 | 37 | 22 | 24 | 9 | 25 | 10 | 23 | 8 | 23 | 8 | -0,52 | ||||||
| 7 |
С 2 11 |
3 2 4 |
595,90 472,45 1475,65 |
1,3 4,0 4,8 |
3,08 1,00 0,83 |
0,63 0,20 0,17 |
32504, 80 60 1,60 |
13 0 17 |
80 75 95 |
3 0 3 |
80 82 1,19 |
0 0 7 |
80 69 1,18 |
7 0 8 |
80 70 1,16 |
6 0 8 |
95 28 19 |
4 14 -32 |
2,52 2,8 -5,44 |
|
| 4,91 | 1,00 | 90 | 30 | 81 | 6 | 87 | 7 | 84 | 15 | 84 | 14 | 50 | -0,12 | |||||||
| 11 |
F 2 7 |
5 6 4 |
2568,90 -1002,95 -1475,65 |
4,4 5,3 4,8 |
0,91 0,75 0,83 |
0,37 0,30 0,33 |
31029, 95 28,95 15 |
37 0 7 |
95 35 25 |
26 3 0 |
95 42 16 |
29 8 0 |
95 29 22 |
27 2 0 |
95 30 19 |
28 3 0 |
95 28 19 |
28 3 0 |
-45 22 31 |
-16,65 6,6 10,23 |
| 2,49 | 1,00 | 39 | 44 | 54 | 29 | 53 | 37 | 51 | 29 | 50 | 31 | 50 | 31 | 0,18 | ||||||
| 2 |
В 7 11 |
1 2 6 |
954,10 -2972,97 -3225,53 |
1,1 4,0 5,3 |
3,64 1,00 0,75 |
0,68 0,18 0,14 |
26716, 1,15 78 1,57 |
25 0 11 |
11,5 82 1,51 |
22 0 10 |
-1 32 -37 |
-0,68 5,76 -5,18 |
||||||||
| 5,39 | 1,00 | 1,14 | 36 | 1,14 | 32 | -0,1 | ||||||||||||||
| 7 |
С 2 11 |
3 2 4 |
872,40 2972,97 -253,55 |
1,3 4,0 4,8 |
3,08 1,00 0,83 |
0,63 0,20 0,17 |
29689, 75 1,12 55 |
13 11 0 |
75 1,11 49 |
16 12 0 |
75 1,11 50 |
16 12 0 |
75 1,11 49 |
16 12 0 |
75 1,11 50 |
16 12 0 |
2 -34 28 |
1,26 -6,8 4,76 |
||
| 4,91 | 1,00 | 79 | 24 | 77 | 28 | 78 | 28 | 77 | 28 | 78 | 28 | -0,78 | ||||||||
| 11 |
F 2 7 |
5 6 4 |
4242,62 3225,53 253,55 |
4,4 5,3 4,8 |
0,91 0,75 0,83 |
0,37 0,30 0,33 |
29942, 1,10 0,67 1,30 |
16 0 21 |
1,10 67 1,34 |
16 0 22 |
1,10 67 1,32 |
16 0 21 |
1,10 67 1,33 |
16 0 22 |
1,10 67 1,32 |
16 0 21 |
-5 38 -28 |
-1,85 11,4 -9,24 |
||
| 2,49 | 1,00 | 1,04 | 37 | 1,05 | 38 | 1,04 | 37 | 1,05 | 38 | 1,04 | 37 | 0,31 | ||||||||