Курсовая работа: Программирование действий над матрицами на языке С++

Государственное образовательное учреждение

высшего профессионального образования

Ульяновский Государственный Университет

Факультет Математики и Информационных технологий

Кафедра информационных технологий

КУРСОВАЯ РАБОТА

Программирование действий над матрицами на языке С++.

Прикладная информатика 08.08.01

Проект выполнил студент

Русин Виктор Александрович

Ульяновск

2010 г.

Содержание

Введение

1. Теоретическая часть

1.1 Описание программы, матрицы

1.2 C++

1.3 Microsoft Visual Studio Express

1.4 Стандартная библиотека шаблонов (STL)

1.5 Vector

1.6 Перегрузка операторов

2. Проектирование и этапы разработки

2.1 Постановка задачи

2.2 Средства разработки

2.3 Описание процесса компиляции и запуска программы

3. Реализация

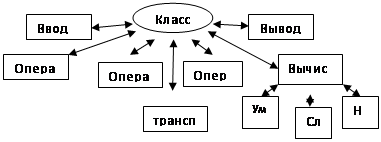
3.1 Структура программы

3.2 Структура класса

Заключение

Литература

Приложение. Исходный код программы. Заголовочные файлы

Введение

На сегодняшний день математическое программирование – важная составляющая всего программирования. Большие и сложные вычисления благодаря простым программам становятся простыми.

В данной курсовой работе создавалась программа для вычислений над матрицами.

В качестве среды программирования выбрана MS Visual Studio 2008 и язык программирования C++.

1 . Теоретическая часть

1.1 Описание программы, матрицы

Ма́трица — математический объект, записываемый в виде прямоугольной таблицы чисел (или элементов кольца) и допускающий алгебраические операции (сложение, вычитание, умножение) между ним и другими подобными объектами. Обычно матрицы представляются двумерными (прямоугольными) таблицами. Иногда рассматривают многомерные матрицы или матрицы непрямоугольной формы.

Операции над матрицами

Пусть aij — элементы матрицы A, а bij — элементы матрицы B.

Линейные операции:

Умножение матрицы A на число λ (обозначение: λA) заключается в построении матрицы B, элементы которой получены путём умножения каждого элемента матрицы A на это число, то есть каждый элемент матрицы B равен

bij = λaij

Сложение матриц A + B есть операция нахождения матрицы C, все элементы которой равны попарной сумме всех соответствующих элементов матриц A и B, то есть каждый элемент матрицы C равен

cij = aij + bij

$A+B=\begin{pmatrix} 2 & 0 & -1\\ 1 & 3 & 0\end{pmatrix}+\begin{pmatrix} 3 & 1 & 0\\ 8 & 2 & 3\end{pmatrix}=\begin{pmatrix}2+3 & 0+1 & -1+0\\1+8 & 3+2 & 0+3\end{pmatrix}=\begin{pmatrix}5 & 1 & -1\\9 & 5 & 3\end{pmatrix}$

Вычитание матриц A − B определяется аналогично сложению, это операция нахождения матрицы C, элементы которой

cij = aij - bij

$A-B=\begin{pmatrix} 2 & 0 & -1\\ 1 & 3 & 0\end{pmatrix}-\begin{pmatrix} 3 & 1 & 0\\ 8 & 2 & 3\end{pmatrix}=\begin{pmatrix}2-3 & 0-1 & -1-0\\1-8 & 3-2 & 0-3\end{pmatrix}=\begin{pmatrix}-1 & -1 & -1\\-7 & 1 & -3\end{pmatrix}$

Сложение и вычитание допускается только для матриц одинакового размера.

Существует нулевая матрица Θ такая, что её прибавление к другой матрице A не изменяет A, то есть

A + Θ = A

Все элементы нулевой матрицы равны нулю.

Умножение матриц (обозначение: AB, реже со знаком умножения $A\times B$ ) — есть операция вычисления матрицы C, элементы которой равны сумме произведений элементов в соответствующей строке первого множителя и столбце второго.

$\! c_{ij} = \sum^n_{k=1} a_{ik} b_{kj}$

В первом множителе должно быть столько же столбцов, сколько строк во втором. Если матрица A имеет размерность $m \times n$ , B — $n \times k$ , то размерность их произведения AB = C есть $m \times k$ .

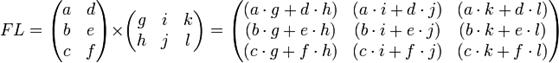
$F L= \begin{pmatrix} a & d \\ b & e \\ c & f \\ \end{pmatrix}\times \begin{pmatrix} g & i & k \\ h & j & l \\ \end{pmatrix}= \begin{pmatrix} (a \cdot g + d \cdot h) & (a \cdot i + d \cdot j) & (a \cdot k + d \cdot l)\\ (b \cdot g + e \cdot h) & (b \cdot i + e \cdot j) & (b \cdot k + e \cdot l)\\ (c \cdot g + f \cdot h) & (c \cdot i + f \cdot j) & (c \cdot k + f \cdot l)\\ \end{pmatrix}$

$A B=\begin{pmatrix} 2 & 3\\ 5 & 7\end{pmatrix}\times\begin{pmatrix} -1 & 2\\ -2 & 3\end{pmatrix}=\begin{pmatrix}2 \cdot (-1) + 3 \cdot (-2) & 2 \cdot 2 + 3 \cdot 3\\5 \cdot (-1) + 7 \cdot (-2) & 5 \cdot 2 + 7 \cdot 3\end{pmatrix}=\begin{pmatrix}-8 & 13\\-19 & 31\end{pmatrix}$

$B A=\begin{pmatrix} -1 & 2\\ -2 & 3\end{pmatrix}\times\begin{pmatrix} 2 & 3\\ 5 & 7\end{pmatrix}=\begin{pmatrix}-1 \cdot 2 + 2 \cdot 5 & -1 \cdot 3 + 2 \cdot 7\\-2 \cdot 2 + 3 \cdot 5 & -2 \cdot 3 + 3 \cdot 7\end{pmatrix}=\begin{pmatrix}8 & 11\\11 & 15\end{pmatrix}$

Возводить в степень можно только квадратные матрицы.

Транспонирование матрицы (обозначение: AT) — операция, при которой матрица отражается относительно главной диагонали, то есть

$a^T_{ij} = a_{ji}$

Если A — матрица размера $m \times n$ , то AT — матрица размера $n \times m$ .

1.2 C++

C++ (Си++) — компилируемый статически типизированный язык программирования общего назначения. Поддерживает разные парадигмы программирования, но, в сравнении с его предшественником — языком Си, — наибольшее внимание уделено поддержке объектно-ориентированного и обобщённого программирования.

Название «C++» происходит от Си (C), в котором унарный оператор ++ обозначает инкремент переменной.

В 1990-х годах язык стал одним из наиболее широко применяемых языков программирования общего назначения.

При создании C++ стремились сохранить совместимость с языком Си. Большинство программ на Си будут исправно работать и с компилятором C++. C++ имеет синтаксис, основанный на синтаксисе Си.

1.3 Microsoft Visual Studio Express

Microsoft Visual Studio Express — линейка бесплатных интегрированных сред разработки, облегчённая версия Microsoft Visual Studio, разработанной компанией Microsoft. Согласно утверждению Microsoft, «Express»-редакции предлагают отлаженную, простую в обучении и использовании среду разработки пользователям, не являющимся профессиональными разработчиками ПО, — любителям и студентам. Последняя версия была выпущена 19 ноября 2007, пакет обновления SP1 — 11 августа 2008. С апреля 2009 года Microsoft прекратила поддержку всех предыдущих версий Visual Studio Express. В апреле 2010 выпущена Visual Studio 2010 Express

1.4 Стандартная библиотека шаблонов (STL)

STL (англ. Standard Template Library) — набор согласованных обобщённых алгоритмов, контейнеров, средств доступа к их содержимому и различных вспомогательных функций.

Стандартная библиотека шаблонов до включения в стандарт C++ была сторонней разработкой, в начале — фирмы HP, а затем SGI. Стандарт языка не называет её «STL», так как эта библиотека стала неотъемлемой частью языка, однако многие люди до сих пор используют это название, чтобы отличать её от остальной части стандартной библиотеки (потоки ввода/вывода (iostream), подраздел Си и др.).

Проект под названием STLPort, основанный на SGI STL, осуществляет постоянное обновление STL, iostream и строковых классов. Некоторые другие проекты также занимаются разработкой частных применений стандартной библиотеки для различных конструкторских задач. Каждый производитель компиляторов C++ обязательно поставляет какую-либо реализацию этой библиотеки, так как она является очень важной частью стандарта и широко используется.

Архитектура STL была разработана Александром Степановым и Менг Ли.

1.5 Vector

Вектор (vector) напоминает нам массив, только он способен расти до произвольного размера, поддерживает информацию о размере. Как и массив к вектору можно обратить воспользовавшись операцией индексирования []. Вот характеристики:

· Доступ к данных с одинаковой скоростью

· Вставка приводит к перемещению элементов

· При расширении данные копируются в другой блок

Как видите вектор оптимален для получения информации, но при большом количестве вставок лучше воспользоваться другими контейнерами, например, списками. Проблема в том, что физически вектор располагается в непрерывной памяти. На C это реализовывали функциями malloc.

Возможно вы уже сталкивались с такой проблемой, что массивы в с++ имеют ограниченный размер, а мы точно не знаем количество элементов, необходимое в массиве. В таких случаях необходимо использовать динамическое программирование. Т.е. выделять память под элементы массива при необходимости добавить какой-либо элемент. В принципе, в с++ это можно реализовать вручную, но зачем? если есть специальный класс - vector. Он позволяет создавать нам массивы переменной длины в зависимости от ситуации.

Для работы с вектором необходимо подключить заголовочный файл:

#include "vector"

Объявить рабочую область:

После этого вектор необходимо объявить, это можно сделать двумя способами.

vector< int > vArray1; vector< int > vArray2(30);

В первом случае указывается пустой вектор, а во втором начальный размер.

Можно получать информацию о параметрах вектора:

· size() - сколько данных храниться

· capacity() - сколько может храниться до изменения размера

· max_size() - максимальный размер обычно равен наиболее большому доступному блоку памяти

1.6 Перегрузка операторов

Перегрузка операторов — в программировании — один из способов реализации полиморфизма, заключающийся в возможности одновременного существования в одной области видимости нескольких различных вариантов применения оператора, имеющих одно и то же имя, но различающихся типами параметров, к которым они применяются.

Реализация

Перегрузка операций предполагает введение в язык двух взаимосвязанных особенностей: возможности объявлять в одной области видимости несколько процедур или функций с одинаковыми именами и возможности описывать собственные реализации операций (то есть знаков операций, обычно записываемых в инфиксной нотации, между операндами). Принципиально реализация их достаточно проста:

Иногда возникает потребность описывать и применять к созданным программистом типам данных операции, по смыслу эквивалентные уже имеющимся в языке. Классический пример — библиотека для работы с комплексными числами. Они, как и обычные числовые типы, поддерживают арифметические операции, и естественным было бы создать для данного типа операции «плюс», «минус», «умножить», «разделить», обозначив их теми же самыми знаками операций, что и для других числовых типов. Запрет на использование определённых в языке элементов вынуждает создавать множество функций с именами вида ComplexPlusComplex, IntegerPlusComplex, ComplexMinusFloat и так далее.

Когда одинаковые по смыслу операции применяются к операндам различных типов, их вынужденно приходится называть по-разному. Невозможность применять для разных типов функции с одним именем приводит к необходимости выдумывать различные имена для одного и того же, что создаёт путаницу, а может и приводить к ошибкам. Например, в классическом языке Си существует два варианта стандартной библиотечной функции нахождения модуля числа: abs() и fabs() — первый предназначен для целого аргумента, второй — для вещественного. Такое положение, в сочетании со слабым контролем типов Си, может привести к труднообнаруживаемой ошибке: если программист напишет в вычислении abs(x), где x — вещественная переменная, то некоторые компиляторы без предупреждений сгенерируют код, который будет преобразовывать x к целому путём отбрасывания дробной части и вычислять модуль от полученного целого числа!

Отчасти проблема решается средствами объектного программирования — когда новые типы данных объявляются как классы, операции над ними могут быть оформлены как методы классов, в том числе и одноимённые (поскольку методы разных классов не обязаны иметь различные имена), но, во-первых, оформление подобным образом операций над значениями разных типов неудобно, а во-вторых, это не решает проблему создания новых операторов.

Средства, позволяющие расширять язык, дополнять его новыми операциями и синтаксическими конструкциями (а перегрузка операций является одним из таких средств, наряду с объектами, макрокомандами, функционалами, замыканиями) превращают его уже в метаязык — средство описания языков, ориентированных на конкретные задачи. С его помощью можно для каждой конкретной задачи построить языковое расширение, наиболее ей соответствующее, которое позволит описывать её решение в наиболее естественной, понятной и простой форме. Например, в приложении к перегрузке операций: создание библиотеки сложных математических типов (векторы, матрицы) и описание операций с ними в естественной, «математической» форме, создаёт «язык для векторных операций», в котором сложность вычислений скрыта, и возможно описывать решение задач в терминах векторных и матричных операций, концентрируясь на сути задачи, а не на технике. Именно из этих соображений подобные средства были в своё время включены в язык Алгол-68.

Чтобы разрешить существование нескольких одноимённых операций, достаточно ввести в язык правило, согласно которому операция (процедура, функция или оператор) опознаются компилятором не только по имени (обозначению), но и по типам их параметров. Таким образом, abs(i), где i объявлено как целое, и abs(x), где x объявлено как вещественное — это две разные операции. Принципиально в обеспечении именно такой трактовки нет никаких сложностей.

Чтобы дать возможность определять и переопределять операции, необходимо ввести в язык соответствующие синтаксические конструкции. Вариантов их может быть достаточно много, но по сути они ничем друг от друга не отличаются, достаточно помнить, что запись вида «<операнд1> <знакОперации> <операнд2>» принципиально аналогична вызову функции «<знакОперации>(<операнд1>,<операнд2>)». Достаточно разрешить программисту описывать поведение операторов в виде функций — и проблема описания решена.

2. Проектирование и этапы разработки

2.1 Постановка задачи

Задача заключается в создании динамического класса для работы с матрицами.

Чтение матриц происходит из файлов в котором они находятся, и после решений все полученные результаты выводятся в другой файл.

Интерфейс.

Интерфейс представлен примитивным меню в котором пользователь выбирает действие. При не открытии одного из файлов выводится ошибка, при успешное выполнение выводится сообщение об успехе.

2.2 Средства разработки

В качестве средства разработки выбран MS Visual Studio 2008 Express.

2.3 Описание процесса компиляции и запуска программы

Для компиляции программы используется IDE MS Visual Studio. В папке с проектом должны присутствовать файлы: file1.txt, file2.txt, file3.txt

Скомпиллированная программа состоит из следующих файлов:

1) папка cnf (конфигурационные файлы);

2) matrix.exe (исполняемый файл);

3. Реализация

3.1 Структура программы

Программа содержит компоненты, отвечающие за:

1) интерфейс,

2) математическую логику,

3) взаимодействие объектов класса,

4) перегрузку операторов.

3.2 Структура класса

Заключение

В ходе выполнения курсовой работы была получена работоспособная программа, удовлетворяющая начальному заданию.

В ходе разработке были проанализированы и использованы следующие технологии:

1) Stl;

2) потоков данных;

3) перегрузка операторов;

В качестве дальнейшего совершенствования программы представляется возможным увеличение функциональности класса и интерфейса (с целью увеличения информативности).

Литература

1. Свободная энциклопедия http://ru.wikipedia.org/

2. Книга У. Форд, У. Топп «Структура данных в С++» ООО «Бином-Пресс»2006г.

3. Беллман Р. Введение в теорию матриц. - М.: Мир, 1969.

4. Курош А.Г.Курс высшей алгебры: Учебник для вузов 15-е изд., стереотип. - М.: Лань, 2006. - 432 с.

5. Дж. Голуб, Ч. Ван Лоун Матричные вычисления. - М.: Мир, 1999.

6. Сайт «Знакомимся с вектором». http://www.cyberguru.ru/

7. Б. Страуструп. «Язык программирования C++. Специальное издание.», 2004 г.

Приложение. Исходный код программы. Заголовочные файлы.

1. matrix.h

#pragma once

#include <list>

#include <vector>

#include <iostream>

using std::vector;

using std::cout;

using std::istream;

using std::ostream;

class _matrix

{

private:

vector< vector<float> > vvf;

int stroka;

int stolbec;

public:

_matrix() {};

_matrix(int str, int stolb)

{

stroka = str;

stolbec = stolb;

vvf.resize(stroka, vector<float>(stolbec));

}

_matrix (const _matrix &obj)

{

stroka = obj.stroka;

stolbec = obj.stolbec;

vvf = obj.vvf;

}

~_matrix()

{

vvf.clear();

}

_matrix& operator+(_matrix &obj2)

{

_matrix* obj = new _matrix(*this);

for(int y = 0; y < obj2.stroka; y++)

for(int x = 0; x < obj2.stolbec; x++)

(*obj)(y, x) = (*this)(y, x) + obj2(y, x);

return *obj;

}

_matrix& operator-(_matrix &obj2)

{

_matrix* obj = new _matrix(*this);

for(int y = 0; y < obj2.stroka; y++)

for(int x = 0; x < obj2.stolbec; x++)

(*obj)(y, x) = (*this)(y, x) - obj2(y, x);

return *obj;

}

_matrix &operator*(_matrix &obj2)

{

_matrix* obj = new _matrix(*this);

for(int y = 0; y < obj->stroka; y++)

for(int x = 0; x < obj->stolbec; x++)

{

(*obj)(y, x) = 0;

for(int k = 0; k < obj->stroka; k++)

(*obj)(y, x) += obj2(k,x) * (*this)(y, k);

}

return *obj;

}

_matrix &operator=(const _matrix &obj)

{

stroka = obj.stroka;

stolbec = obj.stolbec;

vvf = obj.vvf;

return *this;

}

float &operator()(int& i, int& j)

{

return vvf[i][j];

}

_matrix &transpon()

{

_matrix transobj(*this);

for(int y = 0; y < stroka; y++)

for(int x = 0; x < stolbec; x++)

(*this)(y, x) = transobj(x, y);

return *this;

}

vector <float> multvec(int str, float value)

{

vector<float> temp(stroka);

for(int x = 0; x < stroka; x++)

{

temp[x] = value * vvf[str][x];

}

return temp;

}

void norm(int str, float value)

{

for(int x = 0; x < stroka; x++)

{

vvf[str][x] = vvf[str][x]/value;

}

void subvec(int str,vector<float> temp)

{

for(int x = 0; x < stroka; x++)

{

vvf[str][x] = vvf[str][x] - temp[x];

}

_matrix Inversion()

{

_matrix obj(*this);

_matrix invobj(stroka, stolbec);

float f;

for(int y = 0; y < stroka; y++)

invobj(y,y) = 1;

for(int x = 0; x < stolbec; x++)

{

for(int y = 1; y < stroka; y++)

{

if(x < y)

{

f =obj(y, x)/obj(x,x);

obj.subvec(y, obj.multvec(x, f));

invobj.subvec(y, invobj.multvec(x, f));

}

for(int x = stolbec-1; x > -1; x--)

{

for(int y = stroka-1; y > -1; y--)

{

f = obj(x,x);

obj.norm(x, f);//cout << obj;

invobj.norm(x, f);

if(x > y)

{

f =obj(y, x)/obj(x,x);

obj.subvec(y, obj.multvec(x, f));

invobj.subvec(y, invobj.multvec(x, f));

}

cout << obj;

cout << invobj;

return invobj;

}

friend ostream &operator<<(ostream &stream, _matrix &obj);

friend istream &operator>>(istream &stream, _matrix &obj);

};

ostream &operator<<(ostream &stream, _matrix &obj)

{

for(int y = 0; y < obj.stroka; y++)

{

for(int x = 0; x < obj.stolbec; x++)

{

stream << obj(y, x) << " ";

}

stream << "\n";

}

return stream;

}

istream &operator>>(istream &stream, _matrix &obj)

{

for(int y = 0; y < obj.stroka; y++)

for(int x = 0; x < obj.stolbec; x++)

stream >> obj(y, x);

return stream;

}

Приложение 2. Исходный код программы. Файлы cpp.

1. main.cpp

#include <iostream>

#include <conio.h>

#include <fstream>

#include "matrix.h"

using std::cout;

using std::ofstream;

using std::ifstream;

using std::cin;

using std::endl;

int primer1(_matrix &, _matrix &);

int primer2(_matrix &);

int primer1(_matrix &_objA, _matrix &_objB)

{

ofstream fout1;

_matrix _objC;

fout1.open("file3.txt");

if(!fout1)

{

cout << "Error with open output file" << endl;

exit(1);

}

_objC = _objA + _objB;

fout1 << "Сумма: \n";

fout1 << _objC;

_objC = _objA - _objB;

fout1 << "Разность: \n";

fout1 << _objC;

_objC = _objA * _objB;

fout1 << "Произведение: \n";

fout1 << _objC;

return 0;

}

int primer2(_matrix &_objA)

{

ofstream fout1;

fout1.open("file3.txt");

_matrix _objC;

if(!fout1)

{

cout << "nevozmojno open file3" << endl;

exit(1);

}

_objC = _objA.Inversion();

fout1 << "matrix Inversion \n";

fout1 << _objC;

_objC = _objA * _objC;

fout1 << "matrix * matrix.Inversion = \n";

fout1.precision(3);

fout1 << "%f" <<_objC;

return 0;

}

bool freadMatrix(_matrix& mtr, char* fileName)

{

ifstream fin;

fin.open(fileName);

if(!fin) return false;

fin>>mtr;

fin.close();

return true;

}

int menu()

{

int primer;

_matrix objA(5, 5);

_matrix objB(5, 5);

//чтение файлов

if(!freadMatrix(objA, "file1.txt") || !freadMatrix(objB, "file2.txt"))

{

cout << "Error with open input file" << endl;

return 1;

}

cout << "select action \n 1. + - * matrix \n 2. seatch Inversion matrix" << endl;

cin >> primer;

switch(primer)

{

case(1):

primer1(objA, objB);

break;

case(2):

primer2(objA);

break;

}

cout << "ok";

return 0;

}

int main(int argc, char** argv)

{

menu();

_getch();

return 0;

}