Курсовая работа: Разработка программы определительных испытаний

Министерство образования и науки Российской Федерации

Тольяттинский филиал Московского государственного университета пищевых производств

Кафедра Менеджмента пищевых производств

Курсовая работа

по дисциплине «Методы и средства измерений, испытаний и контроля»

на тему «Разработка программы определительных испытаний»

Студентка группы:

Преподаватель:

Тольятти 2008

Содержание

Введение

1 Разработка программы испытаний

1.1Общие положения

1.2 Объект испытаний

1.3 Цель испытаний

1.4 Место проведения и обеспечения испытаний

1.5 Объем и методика испытаний

1.6 Обработка результатов испытаний

1.6.1 Постановка задачи

1.6.2 Вычисление основных характеристик выборки

1.6.3 Формирование статистического ряда и графическое представление данных

1.6.4 Подбор подходящего закона распределения вероятностей

1.6.5 Определение показателей надежности объекта испытаний

1.6.6 Протокол испытаний

2 Пример обработки результатов испытаний для восстанавливаемого объекта испытаний

2.1 Постановка задачи

2.2 Вычисление основных характеристик выборки

2.3 Формирование статистического ряда и графическое представление данных

2.4 Подбор подходящего закона распределения вероятностей

2.5 Определение показателей надежности объекта испытаний

Заключение

Список использованных источников

Введение

Испытанием – это экспериментальное определение количественных и качественных характеристик свойств объекта как результата воздействия на него при его функционировании или моделировании.

Испытания опытных образцов, установочных и первых промышленных партий, контрольные периодические испытания серийной продукции – это основа построения всей системы разработки и постановки продукции на производство.

Постоянное повышение требований к качеству выпускаемой продукции, рост сложности современной техники, создание новых видов продукции с использованием последних достижений науки и техники определили значительное расширение видов испытаний, увеличение их сложности и трудоемкости.

Испытания являются неотъемлемой частью взаимоотношений заказчика и изготовителя продукции, предприятия-изготовителя конечной продукции и предприятий-смежников, поставщика и потребителя при внутреннем и международном товарообмене.

Все испытания по своему назначению разделяют на четыре группы: исследовательские, контрольные, сравнительные и определительные.

Целью данной курсовой работы является определение реального уровня надежности выбранного объекта испытаний – электродвигатель однофазный коллекторный переменного тока типа ДК 60 – 40, предназначенный для привода различных бытовых приборов.

1. Разработка программы испытаний

Программа испытаний – это обязательный для выполнения организационно-методический эксперимент.

Программа устанавливает цели испытаний, объект испытаний, объем и методику проводимых экспериментов, порядок, условия, место и сроки проведения испытаний, ответственность за обеспечение и проведение испытаний, ответственность за оформление протоколов и отчетов по испытаниям.

Немаловажную роль в программе испытаний играет план проведения испытаний. В плане указываются работы необходимые для проведения испытаний, изготовления образцов, приемка образцов, измерение и определение параметров образцов объекта испытаний, подготовка испытательного оборудования, оформление результатов испытаний, согласование утверждения протокола испытаний и др.

Основной задачей определительных испытаний является определение характеристик изделия или материала. Существенным является правильно сформулировать цели испытания.

Цель испытания раскрывает его назначение, которое должно отображаться в наименовании испытаний.

1.1 Общие положения

Настоящая программа испытаний составлена на основании следующих нормативно-технических документов:

- ГОСТ 27.410-87 «Методы контроля показателей надежности и планы контрольных испытаний на надежность»;

- ГОСТ 11828-86 «Машины электрические вращающиеся. Общие методы испытаний»;

- ГОСТ 10159—79 «Машины электрические вращающиеся коллекторные. Методы испытаний»

1.2 Объект испытаний

Главным признаком объекта испытаний является то, что по результатам его испытаний принимается то или иное решение, а именно его годность или выбраковывание, предъявление на следующие испытания, возможность серийного выпуска и т.д.

Объектом испытаний является электродвигатель однофазный коллекторный переменного тока типа ДК 60 – 40.

Таблица 1 – Габаритные установочные и присоединительные размеры электродвигателей

№	Наименование параметра	Тип двигателя
№	Наименование параметра	ДК 60 - 40 - 15 УХЛ4
1	Напряжение питания, В	220±22
2	Частота питания, Гц	50±1
3	Вращаюший момент, Нхм	0,026±0,003
4	Частота вращения, об./мин.	+3000 15000 -1500
5	Ток, А не более	0,48
6	Коэффициент полезного действия, %	45 -6,8
7	Масса двигателя, кг не более	0,35
8	Lmax, мм	90
9	L1, мм	19,5
10	L2, мм	4,5+0,5
11	d, мм	4-0,012
12	Средняя наработка до отказа, не менее, ч	100
13	Средний срок службы двигателя, не менее, лет	10

Электродвигатель однофазный коллекторный переменного тока типа ДК 60 – 40 применяется для привода кофемолок и других бытовых приборов.

1.3 Цель испытаний

Целью испытаний является определение фактических показателей надежности объекта исследования, таких как: среднее время безотказной работы T (средняя наработка до отказа), вероятность безотказной работы объекта в течение времени P(t), вероятность отказа Q(t), плотность распределения времени до отказа f(t), интенсивность отказа λ(t) в момент времени t.

1.4 Место проведения и обеспечение испытаний

Испытательный центр ОАО «ПЭМЗ», аккредитованный Федеральным агентством по техническому регулированию и метрологии для проведения испытаний с целью сертификации.

1.5 Объем и методика испытаний

Испытания проводятся по плану [NUN], согласно которому испытывают одновременно N=100 объектов, отказавшие во время испытаний объекты не восстанавливают и не заменяют, испытания прекращают, когда число отказавших объектов достигло N=100.

1.6 Обработка результатов испытаний

1.6.1 Постановка задачи

Требуется определить показатели надежности объекта испытаний по опытным данным определительных испытаний.

На испытания поставлено N = 100 объектов. Моменты отказов объекта испытаний представлены в таблице 2. Все объекты работают до своего отказа и после отказа не ремонтируются. Требуется определить статистические и теоретические показатели надежности объекта: T, P(t), Q(t), f(t), λ(t).

Таблица 2 – Моменты отказов объектов, в часах

350	244	69	234	145	196	389	23	251	127
226	118	219	204	120	180	406	182	74	240
206	257	181	104	130	341	245	9	226	161
147	71	219	361	162	112	67	182	34	76
143	60	119	190	281	437	226	307	41	148
228	37	296	51	254	44	190	143	795	117
191	14	392	157	16	203	89	346	303	40
377	319	258	37	68	235	385	128	111	640
136	224	174	601	35	71	345	132	197	35
331	83	97	178	328	194	110	120	106	109

1.6.2 Вычисление основных характеристик выборки

Основными числовыми характеристиками выборочной совокупности является: выборочное среднее, выборочная дисперсия, выборочное среднее квадратическое (или стандартное) отклонение, наименьшие и наибольшие значения, размах выборки, асимметрия, эксцесс.

Для расчета указанных характеристик в Excel необходимо поставить курсор в ячейку, в которую будет записано значение характеристики, вызвать соответствующую функцию и в качестве ее аргумента указать блок ячеек со статистическими данными.

Для удобства следующих операций значения случайной величины Z (статистические данные) перепишем на другой лист в прямоугольный блок ячеек, например А1:J10.

Значения вычисляемых характеристик будет располагаться в ячейках F12 по F19.

Таблица 3 – Расчет выборочных характеристик

	A	B	C	D	E		F	G	H	I	J
1	99	91	104	114	97		91	99	101	99	95
2	109	98	119	84	102		120	107	97	110	102
3	88	99	99	104	103		110	96	85	109	89
4	79	100	111	103	89		92	109	99	91	86
5	100	90	102	91	89		95	98	87	117	100
6	95	98	97	107	90		112	85	101	94	87
7	99	93	104	90	90		109	89	95	102	88
8	100	98	93	104	107		98	104	112	100	105
9	115	113	94	110	93		94	82	100	94	102
10	90	94	102	110	90		99	93	87	115	97
11
12	Выборочное среднее					98,68
13	Выборочная дисперсия					76,86626
14	Выборочное ср. квадр. отклонение					8,767341
15	Наименьшее значение					79
16	Наибольшее значение					120
17	Размах выборки					41
18	Асимметрия					0,282254
19	Эксцесс					-0,38419

Вычисление выборочных характеристик осуществляется по формулам:

- выборочное среднее F12 = СРЗНАЧ (A1:J10);

- выборочная дисперсия F13 = ДИСП (A1:J10);

- выборочное среднее квадратическое отклонение

F14 = СТАНДОТКЛОН (A1:J10) или F14 = КОРЕНЬ (F13);

- Наименьшее значение: F15 = МИН(A1:J10);

- Наибольшее значение: F16 = МАКС(A1:J10);

- Размах выборки: F17 = F16-F15;

- Асимметрия: F18 = СКОС(A1:J10);

- Эксцесс: F19 = ЭКСЦЕСС(A1:J10).

1.6.3 Формирование статистического ряда и графическое представление данных

Для наглядного представления статистических данных воспользуемся группировкой. Числовая ось при этом разбивается на интервалы, и для каждого интервала подсчитывается число элементов выборки, которые в него попали. Группировка данных производится в следующей последовательности:

наименьшее значение округляется в меньшую сторону, а наибольшее – в большую сторону до «хороших» чисел хmin и хmax;

выбирается количество групп k, удовлетворяющее неравенству; иногда оно определяется по формуле k=[5lg n]. Если объем выборки n=100, то k=10;

находится шаг по формуле:

где R = хmax - хmin – длина промежутка, в котором содержатся статистические данные;

определяются границы частичных интервалов:

а0 = хmin, а1 = а0 + h, a2 = a1 + h, … , ak = ak-1 + h = хmax;

в каждом интервале вычисляются средние значения

;

для каждого интервала [ai-1,ai], i = 1,2, …,k находятся:

– частоты ni, т.е. число выборочных значений, попавших в интервал;

– относительные частоты ;

– накопленные частоты wi = n1 + n2 + … + ni;

– накопленные относительные частоты .

Для выборочной совокупности (таблица 2) результаты группировки представим в таблице 4. Сначала укажем объем выборки, максимальное и минимальное значение, размах выборки, количество групп и шаг:

А22 = 100, В22 = 120, С22 = 70, D22 = B22 – C22, E22 = 10, F22 = D22/E22.

В ячейках А24:H24 укажем заголовки будущей таблицы. В этой таблице колонки В и С можно заполнить соответствующими формулами, представленными выше, для определения границ интервалов. Колонку D заполним по формуле: D30 = (B25+C25)/2, с последующим копированием в ячейки D26:D34.

Таблица 4 – Группировка статистических данных

	A	B	C	D	E	F	G	H
	n	Xmax	Xmin	R	k	h
22	100	120	70	50	10	5
23
24	Группа	Левая граница	Правая граница	Середина	Частота	Относ. частота	Накоп. частота	Накоп. относ. частота
25	1	70	75	72,5	0	0	0	0
26	2	75	80	77,5	1	0,01	1	0,01
27	3	80	85	82,5	4	0,04	5	0,05
28	4	85	90	87,5	16	0,16	21	0,21
29	5	90	95	92,5	18	0,18	39	0,39
30	6	95	100	97,5	24	0,24	63	0,63
31	7	100	105	102,5	16	0,16	79	0,79
32	8	105	110	107,5	11	0,11	90	0,9
33	9	110	115	112,5	7	0,07	97	0,97
34	10	115	120	117,5	3	0,03	100	1

Для заполнения колонки Е выделим ячейки Е25:Е34 и воспользуемся функцией ЧАСТОТА, указав массив статистических данных и массив правых границ интервалов: { = ЧАСТОТА (А1:J10; C25:C34)}

Одновременным нажатием клавиш заполним остальные выделенные ячейки.

Колонку F заполним с помощью формулы:

F25 = E25/$A$22, с последующим копированием в ячейки F26:F34

Колонку G заполним с помощью формулы:

G25 = E25, G26 = G25 + E26, с последующим копированием в ячейки G32:G39

Колонку H заполним с помощью формулы:

H25 = G25/$A$22, с последующим копированием в ячейки H26:H34

Данные, собранные в таблице 4 наглядно представим с помощью:

полигон частот – графическая зависимость частот (относительных частот) от середины интервалов (рисунок 1).

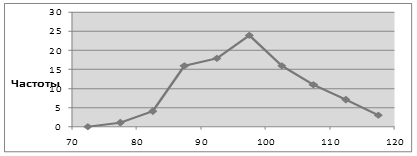
Рисунок 1 – Полигон частот

кумуляты частот – графическая зависимость накопленных частот (накопленных относительных частот) от середины интервалов (рисунок 2).

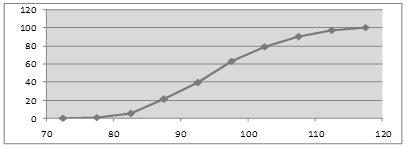
Рисунок 2 – Кумулята частот

1.6.4 Подбор подходящего закона распределения вероятностей

Далее рассмотрим некоторые известные распределения, такие как экспоненциальное, нормальное и гамма-распределение, с целью проверки подчиняется ли наше распределение вероятностей заданному.

Проверка на соответствие данных испытаний распределению производится перебором трех распределений, указанных выше, включая заданное, а именно гамма-распределение.

Чтобы иметь полную информацию о распределении случайной величины, надо знать параметры этого распределения. Таким образом, математическое ожидание случайной величины t равно выборочной средней, а среднее квадратическое отклонение случайной величины t – выборочному среднему квадратическому отклонению. Указанные характеристики находятся в ячейках F12 и F14 соответственно. Поместим эти значения в ячейки А2 и В2 соответственно (таблица 5).

Определим параметры экспоненциального (λ), нормального (m – математическое отклонение и σ – среднее квадратическое отклонение) и гамма-распределения (α и β) в соответствии с формулами:

, ,

B5 = 1/A2;

B8 = A2;

B9 = B2;

B12 = (A2/B2)^2;

B13 = B2^2/A2.

Таблица 5 – Значения плотностей распределения

	A	B	C	D	E
1	Матем. ожидание	Ср. кв. отклон.
2	98,68	8,767340682
3
4	Параметры экспоненциального распределения
5	λ	0,0101
6
7	Параметры нормального распределения
8	m	98,6800
9	σ	8,767340682
10
11	Параметры гамма-распределения
12	α	126,6842
13	β	0,7789
14
15	Середина	Плотность относит. частот	Плотность экспоненц. распред.	Плотность нормал. распред.	Плотность гамма- распред.
16	72,5000	0	0,0049	0,0005	0,0003
17	77,5000	0,002	0,0046	0,0025	0,0019
18	82,5000	0,008	0,0044	0,0083	0,0080
19	87,5000	0,032	0,0042	0,0202	0,0213
20	92,5000	0,036	0,0040	0,0355	0,0374
21	97,5000	0,048	0,0038	0,0451	0,0456
22	102,5000	0,032	0,0036	0,0414	0,0399
23	107,5000	0,022	0,0034	0,0274	0,0259
24	112,5000	0,014	0,0032	0,0131	0,0128
25	117,5000	0,006	0,0031	0,0045	0,0049

В ячейках В16:В25 вычислим плотности относительных частот как частное от деления относительных частот (ячейки F25:F34) на шаг (ячейка $F$22) из таблицы 4.

Плотности экспоненциального, нормального и гамма-распределений рассчитываются в соответствии с формулами:

С16 = ЭКСПРАСП (А16;$B$5;ЛОЖЬ);

D16 = НОРМРАСП (А16;$B$8;$B$9;ЛОЖЬ);

E16 = ГАММАРАСП (А16;$B$12;$B$13;ЛОЖЬ).

Затем копируем их в блок ячеек С17:Е25.

После чего строим гистограмму частот, совмещенную с плотностью каждого из указанных ранее распределений. Графическое изображение гистограммы кривых различных распределений приведены на рисунках 3- 5.

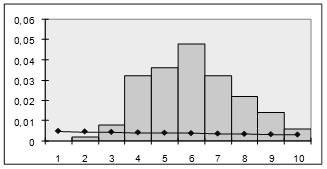
Рисунок 3 – Сглаживание гистограммы плотностью экспоненциального распределения

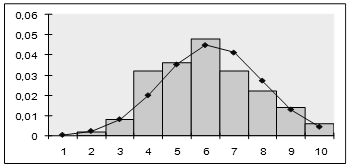
Рисунок 4 – Сглаживание гистограммы плотностью нормального распределения

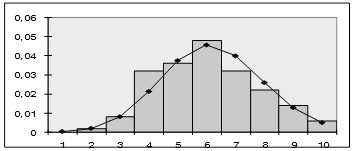
Рисунок 5 – Сглаживание гистограммы плотностью гамма-распределения

Используя критерий χ2, установим, верна ли принятая гипотеза о том, что статистические данные подчиняются нормальному распределению.

Для применения критерия χ2 необходимо, чтобы частоты ni, соответствующие каждому интервалу, были не меньше 5. Для этого при необходимости объединим рядом стоящие интервалы, а их частоты суммируем. Далее вычислим следующую сумму:

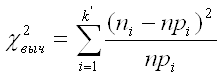где pi – теоретическая вероятность того, что случайная величина Х примет значение из интервала [ai-1,ai].

Предположим, что случайная величина t имеет функцию распределения F(t), поэтому pi = F(ai) – F(ai-1).

Образец расчетов по предыдущей формуле для трех распределений представлен в таблице 6.

В колонке А содержатся левые, а в колонке В – праве границы интервалов. В колонке С находятся соответствующие частоты. В колонке D рассчитываются теоретические вероятности в зависимости от вида распределения.

Для экспоненциального распределения:

D31 = ЭКСПРАСП (B31; $B$5; ИСТИНА) – ЭКСПРАСП (А31; $B$5; ИСТИНА);

Для нормального распределения:

D40 = НОРМРАСП (В40; $B$8; $B$9; ИСТИНА) – НОРМРАСП (А40; $B$8; $B$9; ИСТИНА);

Для гамма-распределения:

D49 = ГАММАРАСП (В49; $B$12; $B$13; ИСТИНА) – ГАММАРАСП (А49; $B$12; $B$13$ ИСТИНА).

В колонке Е рассчитываются слагаемые соотношения по формуле:

Е31 = (С31-100*В31)^2/(100*D31), которая копируется в другие ячейки колонки Е.

После чего для каждого рассмотренного распределения определим итоговые суммы:

Е38 = СУММ(E34:E39);

Е47 = СУММ(E42:E47);

Е56 = СУММ(Е50:Е55).

Которые равны соответственно 659,6862; 5,2199 и 3,8740.

Гипотеза о виде закона распределения должна быть принята, если вычисленное значение χ2выч достаточно мало, а именно не превосходит критического значения χ2кр, которое определяется по распределению χ2 в зависимости от заданного уровня значимости α и числа степеней свободы r=k’ – s – 1. где k’ – количество интервалов после объединения; s – число неизвестных параметров распределения, которые были определены по выборке.

В данном примере r = 7 – 2 – 1 = 2

Критическое значение рассчитывается по формуле:

Е57 = ХИ2ОБР(0,05;4), из таблицы 6 видно, оно равно 9,4877.

Поскольку 5,2199<9,4877, то принимается гипотеза о том, что статистические данные имеют нормальное распределение с параметрами α = = 98,68 и σ = 8,7673 соответственно.

Таблица 6 – Подбор распределения на основе критерия χ2

	А	B	С	D	E
29	Левая граница	Правая граница	Частота	Вероятности	χ²
30				Экспоненциальное распределение
31	70	85	5	0,069374468	0,5411
32	85	90	16	0,020878363	92,7028
33	90	95	18	0,019846835	129,2349
34	95	100	24	0,018866271	259,1934
35	100	105	16	0,017934153	112,5378
36	105	110	11	0,017048088	50,6805
37	110	120	10	0,031610928	14,7957
38	Сумма				659,6862
39				Нормальное распределение
40	70	85	5	0,058804812	0,1318
41	85	90	16	0,101737571	3,3365
42	90	95	18	0,176260064	0,0079
43	95	100	24	0,222500256	0,1376
44	100	105	16	0,204663183	0,9747
45	105	110	11	0,137173828	0,5383
46	110	120	10	0,090811892	0,0930
47	Сумма				5,2199
48				Гамма-распределение
49	70	85	5	0,053672643	0,0251
50	85	90	16	0,107072418	2,6163
51	90	95	18	0,185399233	0,0157
52	95	100	24	0,224931406	0,1009
53	100	105	16	0,197757868	0,7209
54	105	110	11	0,129724735	0,2999
55	110	120	10	0,090713209	0,0951
56	Сумма				3,8740
57	Критическое значение критерия				9,4877

1.6.5 Определение характеристик надежности системы

После подтверждения гипотезы о виде закона распределения, определим характеристики надежности системы. Ббыло установлено, что случайная величина имеет плотность распределения вероятностей:

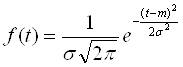
Основными характеристиками надежности невосстанавливаемой системы являются вероятность безотказной работы, и вероятность отказа в течение времени t.

Данные характеристики вычисляются по формулам:

В64 = 1 - НОРМРАСП (А64; $B$8; $B$9; ИСТИНА);

С64 = 1 - В64;

Плотность распределения и интенсивность отказа рассчитаем по следующим формулам:

D64 = НОРМРАСП (А64; $B$8; $B$9; ЛОЖЬ);

E64 = D64/B64.

Далее скопируем формулы в ячейки В64:В74, С64:С74, D64:D74, E64:E74 соответственно.

В результате будет получена таблица вычисленных ранее значений (таблица 7) и построены их графики (рисунки 6,7,8).

Таблица 7 – Значения показателей надежности объекта испытаний

	А	B	C	D	E
63	t	P(t)	Q (t)	f (t)	λ (t)
64	63,611	1,000	0,000	0,000	0,000
65	74,000	0,998	0,002	0,001	0,001
66	84,000	0,953	0,047	0,011	0,012
67	94,000	0,703	0,297	0,039	0,056
68	104,000	0,272	0,728	0,038	0,139
69	114,000	0,040	0,960	0,010	0,245
70	124,000	0,002	0,998	0,001	0,363
71	134,000	0,000	1,000	0,000	0,485

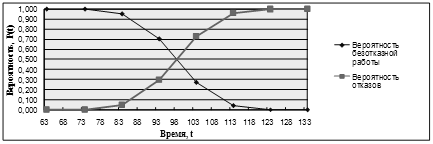
Рисунок 6 – График вероятности безотказной работы и вероятности отказа

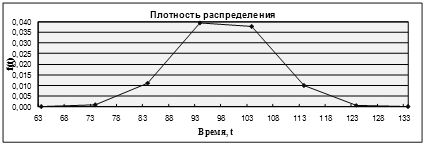
Рисунок 7 – График плотности распределения вероятности

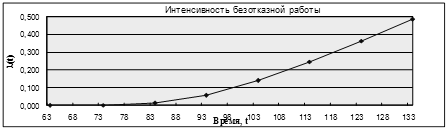
Рисунок 8 – График интенсивности отказа

1.6.6 Протокол испытаний

ИСПЫТАТЕЛЬНЫЙ ЦЕНТР «ПЭМЗ-электро»

аттестат № РОСС RU.0004.13ЛРН02

445030. Тольятти, ул. Свердлова 19

телефон (8482) 33-77-88

e-mail: pemz-elektro@tlt.ru

ПРОТОКОЛ ИСПЫТАНИЙ № 13

ЗАКАЗЧИК:

ОАО «Старт», 445028, г. Тольятти, ул. Революционная 72а.

ПРОИЗВОДИТЕЛЬ ПРОДУКЦИИ:

ООО «Электротех», г. Самара, ул. Новосадовая 3.

ВИД ИСПЫТАНИЯ:

Определение фактических показателей надежности электродвигателя однофазного коллекторного переменного тока типа ДК 60 – 40.

ПРОДОЛЖИТЕЛЬНОСТЬ ИСПЫТАНИЙ:

10.09.2008 г. – 25. 12. 2008 г.

ДОГОВОР №:

По заявке от 01.09.2008 г.

ТЕКСТ: 2 стр.

ЦЕЛЬ ИСПЫТАНИЯ:

Определение реального уровня надежности у предъявляемых объектов по опытным данным определительных испытаний.

ОТБОР ОБРАЗЦОВ:

Дата отбора: 15.09.2008 г.

Место отбора: склад

Другие сведения: отбор образцов и их подготовка к испытаниям по ГОСТ Р 11828-86.

ХАРАКТЕРИСТИКА ОБРАЗЦОВ:

Вид продукции: электродвигатель однофазный коллекторный переменного тока типа ДК 60 – 40.

Другие сведения: средняя наработка до отказа не менее 90 ч.

МЕТОДИКА ИСПЫТАНИЙ:

Испытания проводились по плану [NUN], согласно которому испытывались одновременно 100 объектов, отказавшие во время испытаний объекты не подлежали восстановлению и не заменялись, испытания прекращались, когда число отказавших объектов достигло также 100.

РЕЗУЛЬТАТЫ ИСПЫТАНИЙ:

Значения показателей надежности объекта испытаний приведены в таблице.

t	P(t)	Q (t)	f (t)	λ (t)
63,611	1,000	0,000	0,000	0,000
74,000	0,998	0,002	0,001	0,001
84,000	0,953	0,047	0,011	0,012
94,000	0,703	0,297	0,039	0,056
104,000	0,272	0,728	0,038	0,139
114,000	0,040	0,960	0,010	0,245
124,000	0,002	0,998	0,001	0,363
134,000	0,000	1,000	0,000	0,485

Заключение: Результаты испытаний: электродвигатели соответствуют требованиям по средней продолжительности горения.

Руководитель ИЦ «ПЭМЗ-электро» Д.В. Айдаров

Руководитель группы испытаний ИЦ «ПЭМЗ-электро» А. А. Телепова

2. Пример обработки результатов испытаний для невосстанавливаемого объекта испытаний

Постановка задачи

На испытаниях находится N = 56 объектов с восстановлением. В течение периода Т = 600 часов регистрируются моменты времени отказов элементов (таблица 8). Предполагается, что отказавшие элементы заменяют идентичными по надежности элементами. Требуется определить показатели надежности элемента, характеризующие время его работы между соседними отказами: Т, P(t), Q(t), f(t), λ(t).

Испытания проводятся по плану [NRT], согласно которому одновременно начинают испытания N=56 объектов, отказавшие во время испытаний объекты заменяют новыми, испытания прекращают при истечении времени испытаний или наработки T.

Обработка статистических данных предусматривает их группировку в 10 частичных интервалах (классах). Уровень значимости принять равным 0,05.

Таблица 8 – Время между отказами элементов

Номер элемента	Моменты отказа на периоде времени 600 часов
1	104; 93; 107; 118; 89; 86
2	86; 98; 116; 82; 110; 103
3	106; 112; 94; 83; 98; 91
4	94; 106; 102; 107; 89; 91
5	117; 96; 103; 117; 83
6	94; 92; 107; 108; 106
7	90; 96; 84; 107; 99; 99
8	104; 106; 99; 103; 94; 82
9	99;95; 106; 119; 111
10	109; 118; 104; 95; 98

2.2 Вычисление основных характеристик выборки

Основными числовыми характеристиками выборочной совокупности являются: выборочное среднее, выборочная дисперсия, выборочное среднее квадратическое (или стандартное) отклонение, наименьшее и наибольшее значения, размах выборки, асимметрия, эксцесс.

Значения вычисляемых характеристик расположим в ячейках с F12 по F19, как показано в таблице 9.

Таблица 9 – Расчет выборочных характеристик

	A	B	C	D	E	F
1	104	93	107	118	89	86
2	86	98	116	82	110	103
3	106	112	94	83	98	91
4	94	106	102	107	89	91
5	117	96	103	117	83
6	94	92	107	108	106
7	90	96	84	107	99	99
8	104	106	99	103	94	82
9	99	95	106	119	111
10	109	118	104	95	98
11
12	Выборочное среднее					100,0892857
13	Выборочная дисперсия					100,7373377
14	Выборочное ср. квадр. отклонение					10,03679917
15	Наименьшее значение					82
16	Наибольшее значение					119
17	Размах выборки					37
18	Асимметрия					0,012585618
19	Эксцесс					-0,711512555

Вычислим числовые характеристики выборочной совокупности по формулам:

Выборочное среднее: F12 = CРЗНАЧ(A1:F10);

Выборочная дисперсия: F13 = ДИСП(A1:F10);

Выборочное среднее квадратическое отклонение:

F14 = СТАНДОТКЛОН(A1:F10);

Наименьшее значение: F15 = МИН(A1:F10);

Наибольшее значение: F16 = МАКС(A1:F10);

Размах выборки: F17 = F16-F15;

Асимметрия: F18 = СКОС(A1:F10);

Эксцесс: F19 = ЭКСЦЕСС(A1:F10).

2.3 Формирование статистического ряда и графическое представление данных

Для наглядного представления статистических данных воспользуемся группировкой. Группировка данных производится в той же последовательности, что и в пункте 1.6.2 данной работы.

Для выборочной совокупности (таблица 8) результаты группировки представим в таблице 10. Сначала укажем объем выборки, максимальное и минимальное значение, размах выборки, количество групп и шаг:

А22 = 56, В22 =120, С22 = 80, D22 = B22 – C22, E22 =10, F22 = D22/E22

В этой таблице колонки В и С заполним левыми и правыми границами соответственно. Колонку D заполним по формуле:

D25 = (B25+C25)/2, с последующим копированием в ячейки D26:D34.

Таблица 10 – Группировка статистических данных

	A	B	C	D	E	F	G	H
21	n	Xmax	Xmin	R	k	h
22	56	120	80	40	10	4
23
24	Группа	Левая граница	Правая граница	Середина	Частота	Относ. частота	Накоп. частота	Накоп. относ. частота
25	1	80	84	82	5	0,0892	5	0,0892
26	2	84	88	86	2	0,0357	7	0,125
27	3	88	92	90	6	0,1071	13	0,2321
28	4	92	96	94	9	0,1607	22	0,3928
29	5	96	100	98	7	0,125	29	0,5178
30	6	100	104	102	7	0,125	36	0,6428
31	7	104	108	106	10	0,1785	46	0,8214
32	8	108	112	110	4	0,0714	50	0,8928
33	9	112	116	114	1	0,0178	51	0,9107
34	10	116	120	118	5	0,0892	56	1

Для заполнения колонки Е выделим ячейки Е25:Е34 и воспользуемся функцией ЧАСТОТА, указав массив статистических данных и массив правых границ интервалов: { = ЧАСТОТА (А1:F10; C25:C34)}

Одновременным нажатием клавиш заполним остальные выделенные ячейки.

Колонку F заполним с помощью формулы:

F25 = E25/$A$22, с последующим копированием в ячейки F26:F34

Колонку G заполним с помощью формулы:

G25 = E25, G26 = G25 + E26 с последующим копированием в ячейки G27:G34

Колонку H заполним с помощью формулы:

H25 = G25/$A$22, с последующим копированием в ячейки H26:H34

Данные, собранные в таблице 10 наглядно представим с помощью:

полигон частот – графическая зависимость частот (относительных частот) от середины интервалов (рисунок 9).

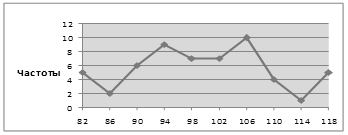
Рисунок 9 – Полигон частот

кумуляты частот – графическая зависимость накопленных частот (накопленных относительных частот) от середины интервалов (рисунок 10).

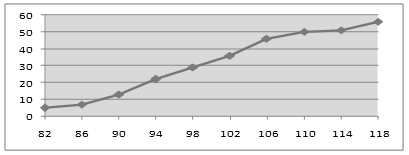
Рисунок 10 – Кумуляты частот

2.4 Подбор подходящего закона распределения вероятностей

Далее рассмотрим некоторые известные распределения, такие как равномерное, нормальное и гамма-распределение, с целью проверки подчиняется ли наше распределение вероятностей заданному.

Проверка на соответствие данных испытаний распределению производится перебором трех распределений, указанных выше, включая заданное, а именно равномерное.

Определим параметры равномерного (a и b), нормального (m – математическое отклонение и σ – среднее квадратическое отклонение), экспоненциального и гамма-распределения (α и β) в соответствии с формулами:

, , , ,

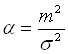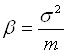B5 = 1/A2;

B8 = A2-В2*КОРЕНЬ(3);

B9 = А2+В2*КОРЕНЬ(3);

B12 = (A2/B2)^2;

B13 = B2^2/A2;

B16 = (A2/B2)^2;

B17 = B2^2/A2.

Таблица 11 – Значения плотностей распределения

	A	B	C	D	E	F
1	Матем. ожидание	Ср. кв. отклон.
2	100,0892	10,0367
3
4	Параметры экспоненциального распределения
5	λ	0,0100
6
7	Параметры равномерного распределения
8	а	82,7050
9	b	117,4735
10
11	Параметры нормального распределения
12	m	100,0893
13	σ	10,0367
14
15	Параметры гамма-распределения
16	α	99,4454
17	β	1,0065
18
19	Середина	Плотность относит. частот	Плотность экспоненц. распред.	Плотность нормал. распред.	Плотность гамма- распред.	Плотность равномер. распред.
20	82	0,0223	0,0044	0,0078	0,0076	0
21	86	0,0089	0,0042	0,0148	0,0156	0,0287
22	90	0,0267	0,0041	0,0240	0,0257	0,0287
23	94	0,0401	0,0039	0,0331	0,0349	0,0287
24	98	0,0312	0,0038	0,0389	0,0397	0,0287
25	102	0,0312	0,0036	0,0390	0,0383	0,0287
26	106	0,0446	0,0035	0,0334	0,0317	0,0287
27	110	0,0178	0,0033	0,0244	0,0229	0,0287
28	114	0,0044	0,0032	0,0152	0,0145	0,0287
29	118	0,0223	0,0031	0,0081	0,0081	0

В ячейках В20:В29 вычислим плотности относительных частот как частное от деления относительных частот (ячейки F25:F34) на шаг (ячейка $F$22) из таблицы 10.

Плотности равномерного, нормального, экспоненциального и гамма-распределений рассчитываются в соответствии с формулами:

С20 = ЭКСПРАСП (А20;$B$5;ЛОЖЬ);

D20 = НОРМРАСП (А20; $B$12; $B$13; ЛОЖЬ);

E20 = ГАММАРАСП (А20; $B$16; $B$17; ЛОЖЬ).

F20 = ЕСЛИ(А20<$B$8; 0; ЕСЛИ(A20>=$B$9; 1/($B$9-$B$8); 0));

Затем копируем их в блок ячеек С21:F21.

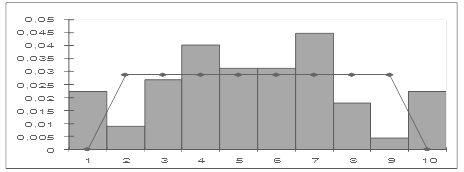
Рисунок 11 – Сглаживание гистограммы плотностью равномерного распределения

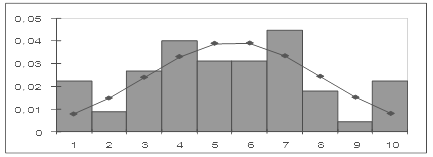
Рисунок 12 – Сглаживание гистограммы плотностью нормального распределения

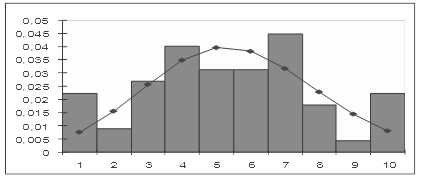
Рисунок 13 – Сглаживание гистограммы плотностью гамма-распределения

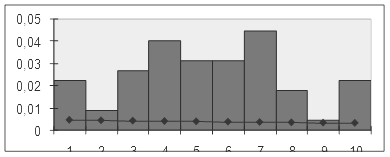
Рисунок 14 – Сглаживание гистограммы плотностью экспоненциального распределения

Используя критерий χ2, установим, верна ли принятая гипотеза о том, что статистические данные подчиняются равномерному распределению, так, чтобы ошибка не превышала заданного уровня значимости α (вероятность того, что будет отвергнута правильная гипотеза).

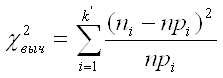где pi – теоретическая вероятность того, что случайная величина Х примет значение из интервала [ai-1,ai].

Предположим, что случайная величина t имеет функцию распределения F(t), поэтому pi = F(ai) – F(ai-1).

Образец расчетов по предыдущей формуле для трех распределений представлен в таблице 6.

Для экспоненциального распределения:

D35 = ЭКСПРАСП (B35; $B$5; ИСТИНА) – ЭКСПРАСП (А35; $B$5; ИСТИНА);

Для равномерного распределения:

D65 = ЕСЛИ (B65<$B$8; 0; ЕСЛИ (B65<=$B$9; (B24-$B$8) / ($B$6-$B$9); 1)) – ЕСЛИ (A24<$B$8; 0; ЕСЛИ (A24<=$B$9; (A24-$B$8) / ($B$6-$B$9); 1));

Для нормального распределения:

D45 = НОРМРАСП (В45; $B$12; $B$13; ИСТИНА) – НОРМРАСП (А45; $B$12; $B$13; ИСТИНА);

Для гамма-распределения:

D55 = ГАММАРАСП (В55; $B$16; $B$17; ИСТИНА) – ГАММАРАСП (А55; $B$16; $B$17; ИСТИНА).

В колонке Е рассчитываются слагаемые соотношения по формуле:

Е35 = (С35-56*D35)^2/(56*D35), которая копируется в другие ячейки колонки Е.

После чего для каждого рассмотренного распределения определим итоговые суммы:

Е43 = СУММ(E35:E42);

Е53 = СУММ(E45:E52);

Е63 = СУММ(Е55:Е62);

Е73 = СУММ(Е65:Е72).

Которые равны соответственно 349,8344; 14,8995; 15,1459; 16,7324.

где k’ – количество интервалов после объединения;

s – число неизвестных параметров распределения, которые были определены по выборке.

В данном примере r = 7 – 2 – 1 = 5

Критическое значение рассчитывается по формуле:

Е74 = ХИ2ОБР(0,05;5), из таблицы 12 видно, оно равно 16,7496.

Поскольку 16,7324<16,7496, то принимается гипотеза о том, что статистические данные имеют равномерное распределение с параметрами a = 82,7050 и b = 117,4735 соответственно.

Таблица 12 – Подбор распределения на основе критерия χ2

	А	B	С	D	E
33	Левая граница	Правая граница	Частота	Вероятности	χ²
34				Экспоненциальное распределение
35	80	84	5	0,0176	16,3293
36	84	92	8	0,0331	20,2945
37	92	96	9	0,01562	75,4446
38	96	100	7	0,01501	45,1229
39	100	104	7	0,01442	47,4663
40	104	108	10	0,01385	109,6166
41	108	116	5	0,02611	8,5589
42	116	120	5	0,01229	27,0014
43	Сумма				349,8344
45				Нормальное распределение
46	80	84	5	0,0317	5,8201
47	84	92	8	0,1556	0,0590
48	92	96	9	0,1317	0,3576
49	96	100	7	0,1546	0,3175
50	100	104	7	0,1551	0,3280
51	104	108	10	0,1331	0,8698
52	108	116	5	0,1588	1,7057
53	116	120	5	0,03281	5,4419
54	Сумма				14,8995
55				Гамма-распределение
56	80	84	5	0,0310	6,1243
57	84	92	8	0,1652	0,1697
58	92	96	9	0,1388	0,1927
59	96	100	7	0,1576	0,3788
60	100	104	7	0,1522	0,2729
61	104	108	10	0,1265	1,1969
62	108	116	5	0,1497	1,3685
63	116	120	5	0,03281	5,4421
64	Сумма				15,1459
65				Равномерное распределение
66	80	84	5	0,03727	4,0719
67	84	92	8	0,2300	1,8522
68	92	96	9	0,1150	1,0151
69	96	100	7	0,1150	0,0482
70	100	104	7	0,1150	0,0482
71	104	108	10	0,1150	1,9643
72	108	116	5	0,2300	4,8254
73	116	120	5	0,0423	2,9070
74	Сумма				16,7324
75	Критическое значение критерия				16,74960237

2.5 Определение показателей надежности объекта испытаний

После подтверждения гипотезы о виде закона распределения, определим показатели надежности объекта.

Таким образом, было установлено, что случайная величина принадлежит множеству с плотностью распределения вероятностей:

Найдем основными показатели надежности. Они вычисляются по формулам:

В78 = ($B$6-А50)/($B$6-$B$5);

С78 = 1 – В78;

Плотность распределения и интенсивность отказа рассчитаем по следующим формулам:

D78 = 1/($B$9-$B$8);

E78 = D78/B78.

Далее скопируем формулы в ячейки В79:В84, С79:С84, D79:D84, E79:E84 соответственно.

В результате будет получена таблица вычисленных ранее значений (таблица 13) и построены их графики (рисунки 14,15,16).

Таблица 13 – Значения показателей надежности объекта испытаний

	А	B	C	D	E
78	82,7050	1	0	0,028761673	0,028761673
79	88	0,847708081	0,152291919	0,028761673	0,033928747
80	93	0,703899717	0,296100283	0,028761673	0,040860469
81	98	0,560091352	0,439908648	0,028761673	0,051351753
82	103	0,416282988	0,583717012	0,028761673	0,069091636
83	108	0,272474623	0,727525377	0,028761673	0,105557253
84	113	0,128666259	0,871333741	0,028761673	0,223537026
85

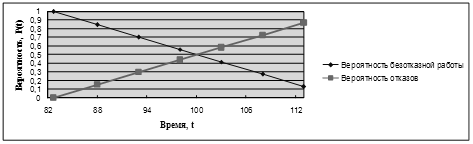
Рисунок 14 – График вероятности безотказной работы и вероятности отказа

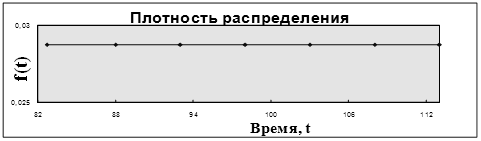
Рисунок 15 – График плотности распределения вероятности

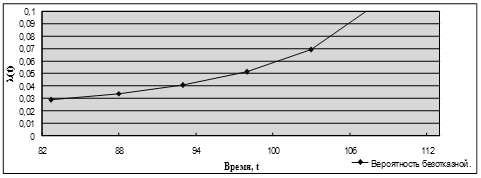
Рисунок 16 – График интенсивности отказа

Заключение

Поставленные перед нами цели курсовой работы по определению фактических показателей надежности невосстанавливаемого объекта испытания – электродвигателя однофазного коллекторного переменного тока типа ДК 60 – 40 – выполнены.