
Рефераты по авиации и космонавтике
Рефераты по административному праву
Рефераты по безопасности жизнедеятельности
Рефераты по арбитражному процессу
Рефераты по архитектуре
Рефераты по астрономии
Рефераты по банковскому делу
Рефераты по сексологии
Рефераты по информатике программированию
Рефераты по биологии
Рефераты по экономике
Рефераты по москвоведению
Рефераты по экологии
Краткое содержание произведений
Рефераты по физкультуре и спорту
Топики по английскому языку
Рефераты по математике
Рефераты по музыке
Остальные рефераты
Рефераты по биржевому делу
Рефераты по ботанике и сельскому хозяйству
Рефераты по бухгалтерскому учету и аудиту
Рефераты по валютным отношениям
Рефераты по ветеринарии
Рефераты для военной кафедры
Рефераты по географии
Рефераты по геодезии
Рефераты по геологии
Рефераты по геополитике
Рефераты по государству и праву
Рефераты по гражданскому праву и процессу
Рефераты по кредитованию
Рефераты по естествознанию
Рефераты по истории техники
Рефераты по журналистике
Рефераты по зоологии
Рефераты по инвестициям
Рефераты по информатике
Исторические личности
Рефераты по кибернетике
Рефераты по коммуникации и связи
Рефераты по косметологии
Рефераты по криминалистике
Рефераты по криминологии
Рефераты по науке и технике
Рефераты по кулинарии
Рефераты по культурологии
Курсовая работа: Решение задач с нормальными законами в системе "Статистика"
Курсовая работа: Решение задач с нормальными законами в системе "Статистика"
СОДЕРЖАНИЕ
Введение
1. Дискриминантный анализ как раздел многомерного статистического анализа
1.1 Методы классификации с обучением
1.2 Линейный дискриминантный анализ
2. Дискриминантный анализ при нормальном законе распределения показателей
3. Примеры решения задач дискриминантным анализом
3.1 Применение дискриминантного анализа при наличии двух обучающих выборок
3.2 Пример решения задачи дискриминантным анализом в системе STATISTICA
Заключение
Список использованных источников
ВВЕДЕНИЕ
Метод дискриминантного анализа впервые был применен в сфере банковской деятельности, а именно - в кредитном анализе. Здесь наиболее четко прослеживается основной подход метода, подразумевающий привлечение прошлого опыта: необходимо определить, чем отличаются заемщики, вернувшие в срок кредит, от тех, кто этого не сделал. Полученная информация должна быть использована при решении судьбы новых заемщиков. Иначе говоря, применение метода имеет цель: построение модели, предсказывающей, к какой из групп относятся данные потребители, исходя из набора предсказывающих переменных (предикторов), измеренных в интервальной шкале. Дискриминатный анализ связан со строгими предположениями относительно предикторов: для каждой группы они должны иметь многомерное нормальное распределение с идентичными ковариационными матрицами.
Основные положения дискриминантного анализа легко понять из представления исследуемой области, как состоящей из отдельных совокупностей, каждая из которых характеризуется переменными с многомерным нормальным распределением. Дискриминантный анализ пытается найти линейные комбинации таких показателей, которые наилучшим образом разделяют представленные совокупности.
При использовании метода дискриминантного анализа главным показателем является точность классификации, и этот показатель можно легко определить, оценив долю правильно классифицированных при помощи прогностического уравнения наблюдений. Если исследователь работает с достаточно большой выборкой, применяется следующий подход: выполняется анализ по части данных (например, по половине), а затем прогностическое уравнение применяется для классификации наблюдений во второй половине данных. Точность прогноза оценивается, т.е. происходит перекрестная верификация. В дискриминантном анализе существуют методы пошагового отбора переменных, помогающие осуществить выбор предсказывающих переменных.
Итак, целью дискриминантного анализа является получение прогностического уравнения, которое можно будет использовать для предсказания будущего поведения потребителей. Например, в отношении клиентов банка существует необходимость на основе некоторого набора переменных (возраст, годовой доход, семейное положение и т.п.) уметь относить их к одной из нескольких взаимоисключающих групп с большими или меньшими рисками не возврата кредита. Исследователь располагает некоторыми статистическими данными (значениями переменных) в отношении лиц, принадлежность которых к определенной группе уже известна. В примере с банком эти данные будут содержать статистику по уже предоставленным кредитам с информацией о том, вернул ли заемщик кредит или нет. Необходимо определить переменные, которые имеют существенное значение для разделения наблюдений на группы, и разработать алгоритм для отнесения новых клиентов к той или иной группе.
1. ДИСКРИМИНАНТНЫЙ АНАЛИЗ
1.1 Методы классификации с обучением
Дискриминантный анализ является разделом многомерного статистического анализа, который включает в себя методы классификации многомерных наблюдений по принципу максимального сходства при наличии обучающих признаков.
В дискриминантном анализе формулируется правило, по которому объекты подмножества подлежащего классификации относятся к одному из уже существующих (обучающих) подмножеств (классов). На основе сравнения величины дискриминантной функции классифицируемого объекта, рассчитанной по дискриминантным переменным, с некоторой константой дискриминации.
В общем случае задача
различения (дискриминации) формулируется следующим образом. Пусть результатом
наблюдения над объектом является реализация k - мерного случайного вектора ![]() . Требуется установить
правило, согласно которому по наблюденному значению вектора х объект относят к
одной из возможных совокупностей
. Требуется установить
правило, согласно которому по наблюденному значению вектора х объект относят к
одной из возможных совокупностей ![]() . Для построения правила
дискриминации все выборочное пространство R значений вектора х разбивается на области
. Для построения правила
дискриминации все выборочное пространство R значений вектора х разбивается на области
![]() так, что
при попадании х в
так, что
при попадании х в ![]() объект относят к совокупности
объект относят к совокупности ![]() .
.
Правило дискриминации
выбирается в соответствии с определенным принципом оптимальности на основе априорной
информации о совокупностях ![]() извлечения объекта из
извлечения объекта из ![]() . При этом
следует учитывать размер убытка от неправильной дискриминации. Априорная
информация может быть представлена как в Виде некоторых сведений о функции мерного
распределения признаков в каждой совокупности, так и в виде выборок из этих
совокупностей. Априорные вероятности
. При этом
следует учитывать размер убытка от неправильной дискриминации. Априорная
информация может быть представлена как в Виде некоторых сведений о функции мерного
распределения признаков в каждой совокупности, так и в виде выборок из этих
совокупностей. Априорные вероятности ![]() могут быть либо заданы, либо нет.
Очевидно, что рекомендации будут тем точнее, чем полнее исходная информация.
могут быть либо заданы, либо нет.
Очевидно, что рекомендации будут тем точнее, чем полнее исходная информация.
С точки зрения применения дискриминантного анализа наиболее важной является ситуация, когда исходная информация о распределении представлена выборками из них. В этом случае задача дискриминации ставится следующим образом.
Пусть ![]() выборка из совокупности
выборка из совокупности
![]() , причем
каждый
, причем
каждый ![]() - й
объект выборки представлен k – мерным вектором параметров
- й
объект выборки представлен k – мерным вектором параметров ![]() . Произведено
дополнительное наблюдение
. Произведено
дополнительное наблюдение ![]() над объектом, принадлежащим одной
из совокупностей
над объектом, принадлежащим одной
из совокупностей ![]() . Требуется построить правило
отнесения наблюдения х к одной из этих совокупностей.
. Требуется построить правило
отнесения наблюдения х к одной из этих совокупностей.
Обычно в задаче различения переходят от вектора признаков, хapaктeризующих объект, к линейной функции от них, дискриминантной функции гиперплоскости, наилучшим образом разделяющей совокупность выборочных точек.
Наиболее изучен случай, когда известно, что распределение векторов признаков в каждой совокупности нормально, но нет информации о параметрах этих распределений. Здесь естественно заменить неизвестные параметры распределения в дискриминантной функции их наилучшими оценками. Правило дискриминации можно основывать на отношении правдоподобия.
Непараметрические методы дискриминации не требуют знаний о точном функциональном виде распределений и позволяют решать задачи дискриминации на основе незначительной априорной информации о совокупностях, что особенно ценно для практических применений.
В параметрических методах эти точки используются для оценки параметров статистических функций распределения. В параметрических методах построения функции, как правило, используется нормальное распределение.
1.2 Линейный дискриминантный анализ
Выдвигаются предположения:
1) имеются разные классы объектов;
2) каждый класс имеет нормальную функцию плотности от k переменных
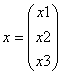 ;
;
![]() , (1.1)
, (1.1)
rде µ (i) - вектор математических ожиданий переменных размерности k;
![]() - ковариационная матрица при n=n;
- ковариационная матрица при n=n;
![]() - обратная матрица.
- обратная матрица.
Матрица ![]() - положительно
определена.
- положительно
определена.
В случае если параметры известны дискриминацию можно провести следующим образом.
Имеются функции плотности
![]() нормально
pacпределенных классов. Задана точка х в пространстве k измерений. Предполагая,
что имеет наибольшую плотность, необходимо отнести точку х к i-му классу. Существует
доказательство, что если априорные вероятности для определяемых точек каждого
класса одинаковы и потери при неправильной классификации i-й группы в качестве
j-й не зависят от i и j, то решающая процедура минимизирует ожидаемые потери
при неправильной классификации.
нормально
pacпределенных классов. Задана точка х в пространстве k измерений. Предполагая,
что имеет наибольшую плотность, необходимо отнести точку х к i-му классу. Существует
доказательство, что если априорные вероятности для определяемых точек каждого
класса одинаковы и потери при неправильной классификации i-й группы в качестве
j-й не зависят от i и j, то решающая процедура минимизирует ожидаемые потери
при неправильной классификации.
Ниже приведен пример оценки параметра многомерногo нормального pacпределения µ и Σ.
µ и Σ мoгyт быть
оценены по выборочным данным: ![]() и
и ![]() для классов. Задано l выборок
для классов. Задано l выборок ![]() из некоторых классов. Математические
ожидания
из некоторых классов. Математические
ожидания ![]() мoгyт
быть оценены средними значениями
мoгyт
быть оценены средними значениями
![]() (1.2)
(1.2)
Несмещенные оценки элементов ковариационной матрицы Σ есть
 (1.3)
(1.3)
Cледовательно, можно определить![]() и
и ![]() по l выборкам в каждом классе при помощи
(1.2), (1.3), получив оценки, точку х необходимо отнести к классу, для которой
функция f(х) максимальна.
по l выборкам в каждом классе при помощи
(1.2), (1.3), получив оценки, точку х необходимо отнести к классу, для которой
функция f(х) максимальна.
Необходимо ввести предположение, что все классы, среди которых должна проводиться дискриминация, имеют нормальное распределение с одной и той же ковариационной матрицей Σ.
В результате существенно упрощается выражение для дискриминантной функции.
Класс, к которому должна принадлежать точка х, можно определить на
основе неравенства
![]()
![]() (1.4)
(1.4)
Необходимо
воспользоваться формулой (1.1) для случая, когда их ковариационные матрицы
равны:![]() , а
, а ![]() ( есть вектор
математических ожиданий класса i. Тогда (1.4) можно представить неравенством их
квадратичных форм
( есть вектор
математических ожиданий класса i. Тогда (1.4) можно представить неравенством их
квадратичных форм
![]() (1.5)
(1.5)
Если имеется два вектора
Z и W, то скалярное произведение можно записать ![]() . В выражении (1.5) необходимо
исключить
. В выражении (1.5) необходимо
исключить ![]() справа
и слева, поменять у всех членов суммы знаки. Теперь преобразовать
справа
и слева, поменять у всех членов суммы знаки. Теперь преобразовать
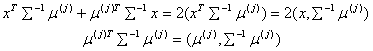
Аналогично проводятся преобразования по индексу i. Необходимо сократить правую и левую часть неравенства (1.5) на 2 и, используя запись квадратичных форм, получается
![]() (1.6)
(1.6)
Необходимо ввести обозначения в выражение (1.6):
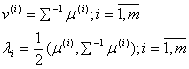
Тогда выражение (1.6) примет вид
![]() (1.7)
(1.7)
Следствие: проверяемая точка х относится к классу i, для которого линейная функция
![]() (1.8)
(1.8)
Преимущество метода линейной дискриминации Фишера заключается в линейности дискриминантной функции (1.8) и надежности оценок ковариационных матриц классов.
Пример
Имеются два класса с
параметрами![]() и
и ![]() . По
выборкам из этих совокупностей объемом n1 n2 получены оценки
. По
выборкам из этих совокупностей объемом n1 n2 получены оценки ![]() и
и ![]() . Первоначально проверяется гипотеза о том, что
ковариационные матрицы
. Первоначально проверяется гипотеза о том, что
ковариационные матрицы ![]()
![]() равны. В случае если оценки
равны. В случае если оценки ![]() и
и ![]() статистически неразличимы, то
принимается, что
статистически неразличимы, то
принимается, что ![]() и строится общая оценка
и строится общая оценка ![]() , основанная на суммарной выборке объемом n1+n2 , после чего строится линейная
дискриминантная функция Фишера (1.8).
, основанная на суммарной выборке объемом n1+n2 , после чего строится линейная
дискриминантная функция Фишера (1.8).
2. ДИСКРИМИНАНТНЫЙ АНАЛИЗ ПРИ НОРМАЛЬНОМ ЗАКОНЕ РАСПРЕДЕЛЕНИЯ ПОКАЗАТЕЛЕЙ
Имеются две генеральные совокупности Х и У, имеющие трехмерный нормальный закон распределения с неизвестными, но равными ковариационными матрицами.
Алгоритм выполнения дискриминантного анализа включает основные этапы:
1. Исходные данные представляются либо в табличной форме в виде q подмножеств (обучающих выборок) Mk и подмножества М0 объектов подлежащих дискриминации, либо сразу в виде матриц X(1), X(2), ..., X(q), размером (nk×p):
Таблица 1
|
Номер подмножества Mk (k = 1, 2, ..., q) |
Номер объекта, i (i = 1, 2, ..., nk) |
Свойства (показатель), j (j = 1, 2, ..., p) |
|||
|
x1 |
x2 |
… |
x0 |
||
|
Подмножество M1 (k = 1) |
1 |
|
|
… |
|
| 2 |
|
|
… |
|
|
| … | … | … | … | … | |
|
n1 |
|
|
… |
|
|
|
Подмножество M2 (k = 2) |
1 |
|
|
… |
|
| 2 |
|
|
… |
|
|
| … | … | … | … | … | |
|
n2 |
|
|
… |
|
|
| … | … | … | … | … | … |
|
Подмножество Mq (k = q) |
1 |
|
|
… |
|
| 2 |
|
|
… |
|
|
| … | … | … | … | … | |
|
nq |
|
|
… |
|
|
|
Подмножество M0, подлежащее дискриминации |
1 |
|
|
… |
|
| 2 |
|
|
… |
|
|
| … | … | … | … | … | |
|
m |
|
|
… |
|
|

где X(k) - матрицы с обучающими признаками (k = 1, 2, ..., q),
X(0) матрица новых m-объектов, подлежащих дискриминации (размером m×p),
р — количество свойств, которыми характеризуется каждый i-й объект.
Здесь должно выполняться условие: общее количество объектов N
множества М должно быть равно сумме количества объектов m (в
подмножестве M0), подлежащих дискриминации, и общего
количества объектов ![]() в обучающих подмножествах:
в обучающих подмножествах:![]() , где q
- количество обучающих подмножеств (q≥2). В реальной практике
наиболее часто реализуется случай q=2, поэтому и алгоритм
дискриминантного анализа приведен для данного варианта.
, где q
- количество обучающих подмножеств (q≥2). В реальной практике
наиболее часто реализуется случай q=2, поэтому и алгоритм
дискриминантного анализа приведен для данного варианта.
2. Определяются ![]() элементы векторов
элементы векторов ![]() средних значений по каждому
j-му признаку для i объектов внутри k-го подмножества (k
= 1, 2):
средних значений по каждому
j-му признаку для i объектов внутри k-го подмножества (k
= 1, 2):

Результаты расчета представляются в виде векторов столбцов![]() :
:

3. Для каждого обучающего подмножества рассчитываются ковариационные матрицы S(k) (размером p×p):
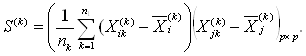
4. Рассчитывается объединенная ковариационная матрица ![]() по формуле:
по формуле:
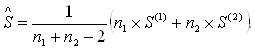
5. Рассчитывается матрица ![]() обратная к объединенной ковариационной
матрице
обратная к объединенной ковариационной
матрице![]() :
:

где |![]() |—
определитель матрицы
|—
определитель матрицы ![]() , (причем
, (причем![]() ),
), ![]() - присоединенная матрица,
элементы которой являются алгебраическими дополнениями элементов матрицы
- присоединенная матрица,
элементы которой являются алгебраическими дополнениями элементов матрицы ![]() .
.
6. Рассчитывается вектор-столбец  дискриминантных множителей с
учетом всех элементов обучающих подмножеств по формуле:
дискриминантных множителей с
учетом всех элементов обучающих подмножеств по формуле: ![]()
Данная расчетная формула получена с помощью метода наименьших квадратов из условия обеспечения наибольшего различия между дискриминантными функциями. Наилучшее разделение двух обучающих подмножеств обеспечивается сочетанием минимальной внутригрупповой вариации и максимальной межгрупповой вариации.
7. По каждому i-му объекту (i = 1, 2, ..., N) множества М определяется соответствующее значение дискриминантной функции:
![]()
8. По совокупности найденных значений F(k) рассчитываются средние значения для каждого подмножества Mk:

9. Определяется общее среднее (константа дискриминации) для дискриминантных функций
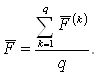
10. Выполняется распределение (дискриминация) объектов подмножества М0 подлежащих дискриминации по обучающим выборкам М1 и М2. С этой целью рассчитанные и п. 7 по каждому i-му объекту значения дискриминантных функций
![]()
сравниваются с величиной ![]() общего среднего. На основе
сравнения данный объект относят к одному из обучающих подмножеств.
общего среднего. На основе
сравнения данный объект относят к одному из обучающих подмножеств.
Если ![]() ,
то i-й объект подмножества М0 относят к подмножеству М1,
при
,
то i-й объект подмножества М0 относят к подмножеству М1,
при ![]() >0
и к подмножеству М2 при
>0
и к подмножеству М2 при ![]() <0. Если же
<0. Если же ![]() <
<![]() , то заданный объект
относят к подмножеству М1, при
, то заданный объект
относят к подмножеству М1, при ![]() < 0 и к подмножеству М2
в противном случае.
< 0 и к подмножеству М2
в противном случае.
11. Далее делается оценка качества распределения новых объектов, для чего оценивается вклад переменных в дискриминантную функцию.
Влияние признаков на значение дискриминантной функции и результаты классификации может оцениваться по дискриминантным множителям (коэффициентам дискриминации), по дискриминантным нагрузкам признаков или по дискриминантной матрице.
Дискриминантные множители зависят от масштабов единиц измерения признаков, поэтому они не всегда удобны для оценки.
Дискриминантные нагрузки более надежны в оценке признаков, они вычисляются как парные линейные коэффициенты корреляции между рассчитанными уровнями дискриминантной функции F и признаками, взятыми для ее построения.
Дискриминантная матрица характеризует меру соответствия результатов классификации фактическому распределению объектов по подмножествам и используется для оценки качества анализа. В этом случае дискриминантная функция F формируется по данным объектов (с измеренными p признаками) обучающих подмножеств, а затем проверяется качество этой функции путем сопоставления фактической классовой принадлежности объектов с той, что получена в результате формальной дискриминации.
3. ПРИМЕРЫ ДИСКРИМИНАНТНОГО АНАЛИЗА
3.1 Применение дискриминантного анализа при наличии двух обучающих выборок (q=2)
Имеются данные по двум группам промышленных предприятий отрасли: Х1 - среднегодовая стоимость основных производственных фондов, млн. д.ед.; Х2 — среднесписочная численность персонала, тыс. чел.; Х3 — балансовая прибыль млн. д.ед.
Исходные данные представлены в таблице 2.
Таблица 2
|
Номер группы Mk (k =1, 2) |
Номер предприятия, i (i = 1, 2, ..., nk) |
Свойства (показатель), j (j = 1, 2, ..., p) |
|||
|
Х1 |
Х2 |
Х3 |
|||
|
Группа 1, M1 (k = 1) |
1 | 224,228 | 17,115 | 22,981 | |
| 2 | 151,827 | 14,904 | 21,481 | ||
| 3 | 147,313 | 13,627 | 28,669 | ||
| 4 | 152,253 | 10,545 | 10,199 | ||
|
Группа 2, M2 (k = 2) |
1 | 46,757 | 4,428 | 11,124 | |
| 2 | 29,033 | 5,51 | 6,091 | ||
| 3 | 52,134 | 4,214 | 11,842 | ||
| 4 | 37,05 | 5,527 | 11,873 | ||
| 5 | 63,979 | 4,211 | 12,860 | ||
|
Группа предприятий M0, подлежащих дискриминации |
1 | 55,451 | 9,592 | 12,840 | |
| 2 | 78,575 | 11,727 | 15,535 | ||
| 3 | 98,353 | 17,572 | 20,458 | ||
Необходимо провести классификацию (дискриминацию) трех новых предприятий, образующих группу М0 с известными значениями исходных переменных.
Решение:
1. Значения исходных переменных для обучающих подмножеств M1 и M2 (групп предприятий) записываются в виде матриц X(1) и X(2) :
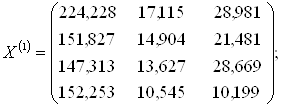
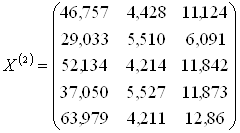
и для подмножества M0 группы предприятий, подлежащих классификации в виде матрицы X(0):
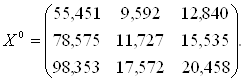
Общее количество предприятий, составляющих множество М, будет равно N = 3+4+5 = 12 ед.
2. Определяются элементы векторов ![]() средних значений по j
признакам для i-х объектов по каждой k-й выборке (k = 1,
2), которые представляются в виде двух векторов
средних значений по j
признакам для i-х объектов по каждой k-й выборке (k = 1,
2), которые представляются в виде двух векторов ![]() (по количеству обучающих выборок):
(по количеству обучающих выборок):
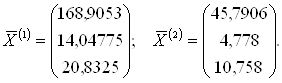
3. Для каждого обучающего подмножества M1 и M2 рассчитываются ковариационные матрицы Sk (размером р×р):
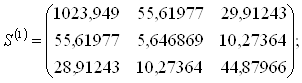

4. Рассчитывается объединенная ковариационная матрица:
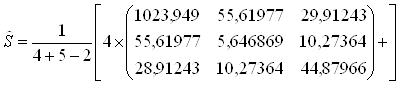
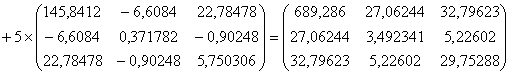
5. Рассчитывается матрица ![]() обратная к объединенной ковариационной
матрице:
обратная к объединенной ковариационной
матрице:
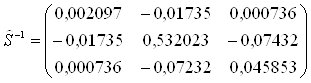
6. Рассчитываются дискриминантные множители (коэффициенты дискриминантной функции) по всем элементам обучающих подмножеств:
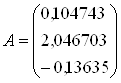
7. Для каждого i-го объекта k-го подмножества М определяется значение дискриминантной функции:
F1(1)=0,104743×224,228+2,046703×17,115+(-0,13635)×22,981=55,38211;
F2(1)=0,104743×151,827+2,046703×14,904+(-0,13635)×21,481=43,47791;
F3(1)=0,104743×147,313+2,046703×13,627+(-0,13635)×28,669=39,41138;
F4(2)=0,104743×152,253+2,046703×10,545+(-0,13635)×10,199=36,13924;
F1(2)=0,104743×46,757+2,046703×4,428+(-0,13635)×11,124=12,44351;
………………………………………………………………………………..
F5(2)=0,104743×63,979+2,046703×4,211+(-0,13635)×12,860=13,56655.
8. По совокупности найденных значений F(k)
рассчитываются средние значения ![]() для каждого подмножества Mk:
для каждого подмножества Mk:
![]()
![]()
9. Определяется общее среднее (константа дискриминации) для дискриминантных функций:
![]()
10. Выполняется распределение объектов подмножества М0 по обучающим подмножествам М1 и М2, для чего по каждому объекту (i = 1, 2, 3) рассчитываются дискриминантные функции:
F1(0)=0,104743×55,451+2,046703×9,592+(-0,13635)×12,840=23,68661
F2(0)=0,104743×78,575+2,046703×11,727+(-0,13635)×15,535=30,11366
F3(0)=0,104743×98,353+2,046703×17,572+(-0,13635)×20,458=23,68661
Затем рассчитанные значения дискриминантных функций F(0) сравниваются с общей средней F=28,3556.
Поскольку ![]() , то i-й объект
подмножества М0 относят к подмножеству М1
при
, то i-й объект
подмножества М0 относят к подмножеству М1
при![]() > 0
и к подмножеству М2 при
> 0
и к подмножеству М2 при ![]() <0. С учетом этого в данном
примере предприятия 2 и 3 подмножества М0 относятся к М1,
а предприятие 1 относится к М2.
<0. С учетом этого в данном
примере предприятия 2 и 3 подмножества М0 относятся к М1,
а предприятие 1 относится к М2.
Если бы выполнялось условие ![]() , то объекты М0
относились к подмножеству М1, при
, то объекты М0
относились к подмножеству М1, при ![]() и к подмножеству М2
в противном случае.
и к подмножеству М2
в противном случае.
11. Оценку качества распределения новых объектов выполним путем сравнения
с константой дискриминации F
значений дискриминантных функций Fi(k)=обучающих
подмножеств М1 и М2. Поскольку для всех найденных
значений выполняются неравенства![]() , и
, и ![]() , то можно предположить о
правильном распределении объектов и уже существующих двух классах и верно
выполненной классификации объектов подмножества М0.
, то можно предположить о
правильном распределении объектов и уже существующих двух классах и верно
выполненной классификации объектов подмножества М0.
3.2 Пример решения задачи дискриминантным анализом в системе STATISTICA
Исходя из данных по 10 странам (рис. 3.1), которые были выбраны и отнесены к соответствующим группам экспертным методом (по уровню медицинского обслуживания), необходимо по ряду показателей классифицировать еще две страны: Молдавия и Украина.
Исходными показателями послужили:
Х1 – Количество человек, приходящихся на одного врача;
Х2 – Смертность на 1000 человек;
Х3 – ВВП, рассчитанный по паритету покупательной способности на душу населения (млн. $);
Х4 – Расходы на здравоохранение на душу населения ($).
Уровень медицинского обслуживания стран подразделяется на:
- высокий;
- средний (удовлетворительный);
- низкий.
|
Кол-во чел. на 1 врача |
Расх. на здрав. |
ВВП |
Смертность |
Класс |
|
|
Азербайджан |
256 | 99 | 3000 | 9,6 | низкий |
|
Армения |
198 | 152 | 3000 | 9,7 | низкий |
|
Белоруссия |
222 | 157 | 7500 | 14 | высокий |
|
Грузия |
182 | 152 | 4600 | 14,6 | удовлетворительный |
|
Казахстан |
265 | 154 | 5000 | 10,6 | удовлетворительный |
|
Киргизия |
301 | 118 | 2700 | 9,1 | низкий |
|
Россия |
235 | 159 | 7700 | 13,9 | высокий |
|
Таджикистан |
439 | 100 | 1140 | 8,6 | низкий |
|
Туркмения |
320 | 125 | 4300 | 9 | удовлетворительный |
|
Узбекистан |
299 | 116 | 2400 | 8 | низкий |
Рис. 3.1
Используя вкладку анализ, далее многомерный разведочный анализ, необходимо выбрать дискриминантный анализ. На экране появится панель модуля дискриминантный анализ, в котором вкладка переменные позволяет выбрать группирующую и независимые переменные. В данном случае группирующая переменная 5 (класс), а независимыми переменными выступят 1-4 (кол-во человек на 1 врача; расходы на здравоохранение; ВВП на душу населения; смертность).
В ходе вычислений системой получены результаты:
Вывод результатов показывает:
- число переменных в модели – 4;
- значение лямбды Уилкса – 0,0086739;
- приближенное значение F – статистики, связанной с лямбдой Уилкса – 9,737242;
- уровень значимости F – критерия для значения 9,737242.
Значение статистики Уилкса лежит в интервале [0,1]. Значения статистики Уилкса, лежащие около 0, свидетельствуют о хорошей дискриминации, а значения, лежащие около 1, свидетельствуют о плохой дискриминации. По данным показателя значение лямбды Уилкса, равного 0,0086739 и по значению F – критерия равного 9,737242, можно сделать вывод, что данная классификация корректная.
В качестве проверки корректности обучающих выборок необходимо посмотреть результаты матрицы классификации (рис. 3.2).
| Матрица классификации . Строки: наблюдаемые классы Столбцы: предсказанные классы | ||||
|
Процент |
низкий |
высокий |
удовлетв |
|
|
низкий |
100,0000 | 5 | 0 | 0 |
|
высокий |
100,0000 | 0 | 2 | 0 |
|
удовлетв |
100,0000 | 0 | 0 | 3 |
|
Всего |
100,0000 | 5 | 2 | 3 |
Рис. 3.2
Из матрицы классификации можно сделать вывод, что объекты были правильно отнесены экспертным способом к выделенным группам. Если есть объекты, неправильно отнесенные к соответствующим группам, можно посмотреть классификацию наблюдений (рис.3.3).
| Классификация наблюдений. Неправильные классификации отмечены * | ||||
|
Наблюд. |
1 |
2 |
3 |
|
|
Азербайджан |
низкий | низкий | удовлетв | высокий |
|
Армения |
низкий | низкий | удовлетв | высокий |
|
Белоруссия |
высокий | высокий | низкий | удовлетв |
|
Грузия |
удовлетв | удовлетв | низкий | высокий |
|
Казахстан |
удовлетв | удовлетв | низкий | высокий |
|
Киргизия |
низкий | низкий | удовлетв | высокий |
|
Россия |
высокий | высокий | низкий | удовлетв |
|
Таджикистан |
низкий | низкий | удовлетв | высокий |
|
Туркмения |
удовлетв | удовлетв | низкий | высокий |
|
Узбекистан |
низкий | низкий | удовлетв | высокий |
Рис. 3.3
В таблице классификации наблюдений, некорректно отнесенные объекты помечаются звездочкой (*). Таким образом, задача получения корректных обучающих выборок состоит в том, чтобы исключить из обучающих выборок те объекты, которые по своим показателям не соответствуют большинству объектов, образующих однородную группу.
В результате проведенного анализа общий коэффициент корректности обучающих выборок должен быть равен 100% (рис. 3.2).
На основе полученных обучающих выборок можно проводить повторную классификацию тех объектов, которые не попали в обучающие выборки, и любых других объектов, подлежащих группировке.
Для этого необходимо в окне диалогового окна результаты анализа дискриминантных функций нажать кнопку функции классификации. Появится окно (рис. 3.4), из которого можно выписать классификационные функции для каждого класса.
| Функции классификации | |||
|
низкий |
высокий |
удовлетв |
|
|
Кол-во чел на 1 врача |
1,455 | 2,35 | 1,834 |
|
Расх на здрав |
1,455 | 1,98 | 1,718 |
|
ВВП |
0,116 | 0,20 | 0,153 |
|
Смертность |
29,066 | 46,93 | 36,637 |
|
Конст-та |
-576,414 | -1526,02 | -921,497 |
Рис. 3.4
Таблица 3
Классификационные функции для каждого класса
| Низкий класс | = -576,414+1,455*кол-во чел на 1 врача+1,455*расх на здра+0,116*ВВП+29,066*смертность |
| Высокий класс | =-1526,02+2,35*кол-во чел на 1 врача+1,98*расх на здрав+0,20*ВВП+46,93*смертность |
| Удовлетворительный класс | =-921,497+1,834*кол-во чел на 1 врача+1,718*расх на здра+0,153*ВВП+36,637*смертность |
С помощью этих функций можно будет в дальнейшем классифицировать новые случаи. Новые случаи будут относиться к тому классу, для которого классифицированное значение будет максимальное.
Необходимо определить принадлежность стран Молдавия и Украина, подставив значения соответствующих показателей в формулы (Таблица 4).
Таблица 4
| Страна | Кол-во человек на 1 врача | Расходы на здравоохранение | ВВП на душу населения | Смертность | Высокий | Низкий | Удовлетворительный | Класс |
| Молдавия | 251 | 143 | 2500 | 12,6 | 438,29 |
653,09 |
628,64 | Низкий |
| Украина | 224 | 131 | 3850 | 16,4 | 880,23 | 863,39 |
904,27 |
Удовл. |
ЗАКЛЮЧЕНИЕ
В данной курсовой работе был рассмотрен такой метод многомерного статистического анализа как дискриминантный. В дискриминантном анализе изучены: основные понятия, цели и задачи дискриминантного анализа. А также определение числа и вида дискриминирующих функций, и классификация объектов с помощью функции расстояния.
Для данного метода приведены примеры решения задач с использованием ППП STATISTICA.
СПИСОК ИСПОЛЬЗОВАННЫХ ИСТОЧНИКОВ
1. Баранова, Т.А. Многомерные статистические методы. Корреляционный анализ. [Текст]: Метод. указания / Иван. гос. хим.-технол. ун-т. / Т.А. Баранова. – Иваново, 9 - 40 с.
2. Буреева, Н.Н. Многомерный статистический анализ с использованием ППП “STATISTICA” [Текст] / Н.Н. Буреева. - Нижний Новгород, 2007. -112с.
3. Дубров, А.М. Многомерные статистические методы и основы эконометрики. [Текст]: Учебное пособие / А.М. Дубров. - М.: МЭСИ, 2008.- 79 с.
4. Калинина, В.Н. Введение в многомерный статистический анализ [Текст]: Учебное пособие / В.Н. Калинина.- ГУУ. – М., 2010. – 66 с.