Реферат: Динамические структуры данных: двоичные деревья

Дерево — это совокупность элементов, называемых узлами (при этом один из них определен как корень), и отношений (родительский–дочерний), образующих иерархическую структуру узлов. Узлы могут являться величинами любого простого или структурированного типа, за исключением файлового. Узлы, которые не имеют ни одного последующего узла, называются листьями.

В двоичном (бинарном) дереве каждый узел может быть связан не более чем двумя другими узлами. Рекурсивно двоичное дерево определяется так: двоичное дерево бывает либо пустым (не содержит ни одного узла), либо содержит узел, называемый корнем, а также два независимых поддерева — левое поддерево и правое поддерево.

Двоичное дерево поиска может быть либо пустым, либо оно обладает таким свойством, что корневой элемент имеет большее значение узла, чем любой элемент в левом поддереве, и меньшее или равное, чем элементы в правом поддереве. Указанное свойство называется характеристическим свойством двоичного дерева поиска и выполняется для любого узла такого дерева, включая корень. Далее будем рассматривать только двоичные деревья поиска. Такое название двоичные деревья поиска получили по той причине, что скорость поиска в них примерно такая же, что и в отсортированных массивах: O(n) = C • log2n (в худшем случае O(n) = n).

Пример. Для набора данных 9, 44, 0, –7, 10, 6, –12, 45 построить двоичное дерево поиска.

Согласно определению двоичного дерева поиска число 9 помещаем в корень, все значения, меньшие его — на левое поддерево, большие или равные — на правое. В каждом поддереве очередной элемент можно рассматривать как корень и действовать по тому же алгоритму. В итоге получаем

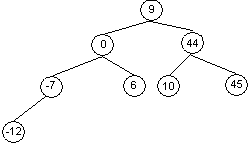
Пример построения двоичного дерева поиска

Выделим типовые операции над двоичными деревьями поиска:

добавление элемента в дерево;

удаление элемента из дерева;

обход дерева (для печати элементов и т.д.);

поиск в дереве.

Поскольку определение двоичного дерева рекурсивно, то все указанные типовые операции могут быть реализованы в виде рекурсивных подпрограмм (на практике именно такой вариант чаще всего и применяется). Отметим лишь, что использование рекурсии замедляет работу программы и расходует лишнюю память при её выполнении.

Пусть двоичное дерево поиска описывается следующим типом

Type BT=LongInt; U = ^BinTree; BinTree = Record Inf : BT; L, R : U End;

Покажем два варианта добавления элемента в дерево: итеративный и рекурсивный.

{Итеративный вариант добавления элемента в дерево, Turbo Pascal}

Procedure InsIteration(Var T : U; X : BT);

Var vsp, A : U;

Begin

New(A); A^.Inf := X; A^.L:=Nil; A^.R := Nil;

If T=Nil Then T:=A

Else Begin vsp := T;

While vsp <> Nil Do

If A^.Inf < vsp^.Inf

Then

If vsp^.L=Nil Then Begin vsp^.L:=A; vsp:=A^.L End Else vsp:=vsp^.L

Else

If vsp^.R = Nil Then Begin vsp^.R := A; vsp:=A^.R End Else vsp := vsp^.R;

End

End;

{Рекурсивный вариант добавления элемента в дерево, Turbo Pascal}

Procedure InsRec(Var Tree : U; x : BT);

Begin

If Tree = Nil

Then Begin

New(Tree);

Tree^.L := Nil;

Tree^.R := Nil;

Tree^.Inf := x

End

Else If x < Tree^.inf

Then InsRec(Tree^.L, x)

Else InsRec(Tree^.R, x)

End;

Аналогично на C++.

typedef long BT;

struct BinTree{

BT inf;

BinTree *L; BinTree *R;

};

/* Итеративный вариант добавления элемента в дерево, C++ */

BinTree* InsIteration(BinTree *T, BT x)

{ BinTree *vsp, *A;

A = (BinTree *) malloc(sizeof(BinTree));

A->inf=x; A->L=0; A->R=0;

if (!T) T=A;

else {vsp = T;

while (vsp)

{if (A->inf < vsp->inf)

if (!vsp->L) {vsp->L=A; vsp=A->L;}

else vsp=vsp->L;

else

if (!vsp->R) {vsp->R=A; vsp=A->R;}

else vsp=vsp->R;

}

return T;

}

/* Рекурсивный вариант добавления элемента в дерево, C++ */

BinTree* InsRec(BinTree *Tree, BT x)

{

if (!Tree) {Tree = (BinTree *) malloc(sizeof(BinTree));

Tree->inf=x; Tree->L=0; Tree->R=0;

}

else if (x < Tree->inf) Tree->L=InsRec(Tree->L, x);

else Tree->R=InsRec(Tree->R, x);

return Tree;

}

Существует несколько способов обхода (прохождения) всех узлов дерева. Три наиболее часто используемых из них называются обход в прямом (префиксном) порядке, обход в обратном (постфиксном) порядке и обход во внутреннем порядке (или симметричный обход). Каждый из обходов реализуется с использованием рекурсии.

Ниже приведены подпрограммы печати элементов дерева с использованием обхода двоичного дерева поиска в обратном порядке.

{Turbo Pascal}

Procedure PrintTree(T : U);

begin

if T <> Nil

then begin PrintTree(T^.L); write(T^.inf : 6); PrintTree(T^.R) end;

end;

// C++

void PrintTree(BinTree *T)

{

if (T) {PrintTree(T->L); cout << T->inf<< " "; PrintTree(T->R);}

}

Реализуем функцию, возвращающую true (1), если элемент присутствует в дереве, и false (0) — в противном случае.

{Turbo Pascal}

function find(Tree : U; x : BT) : boolean;

begin

if Tree=nil then find := false

else if Tree^.inf=x then Find := True

else if x < Tree^.inf

then Find := Find(Tree^.L, x)

else Find := Find(Tree^.R, x)

end;

/* C++ */

int Find(BinTree *Tree, BT x)

{ if (!Tree) return 0;

else if (Tree->inf==x) return 1;

else if (x < Tree->inf) return Find(Tree->L, x);

else return Find(Tree->R, x);

}

По сравнению с предыдущими задача удаления узла из дерева реализуется несколько сложнее. Можно выделить два случая удаления элемента x (случай отсутствия элемента в дереве является вырожденным):

1) узел, содержащий элемент x, имеет степень не более 1 (степень узла — число поддеревьев, выходящих из этого узла);

2) узел, содержащий элемент x, имеет степень 2.

Случай 1 не представляет сложности. Предыдущий узел соединяется либо с единственным поддеревом удаляемого узла (если степень удаляемого узла равна 1), либо не будет иметь поддерева совсем (если степень узла равна 0).

Намного сложнее, если удаляемый узел имеет два поддерева. В этом случае нужно заменить удаляемый элемент самым правым элементом из его левого поддерева.

{Turbo Pascal}

function Delete(Tree: U; x: BT) : U;

var P, v : U;

begin

if (Tree=nil)

then writeln('такого элемента в дереве нет!')

else if x < Tree^.inf then Tree^.L := Delete(Tree^.L, x) {случай 1}

else

if x > Tree^.inf

then Tree^.R := Delete(Tree^.R, x) {случай 1}

else

begin {случай 1}

P := Tree;

if Tree^.R=nil

then Tree:=Tree^.L

else if Tree^.L=nil

then Tree:=Tree^.R

else begin

v := Tree^.L;

while v^.R^.R <> nil do v:= v^.R;

Tree^.inf := v^.R^.inf;

P := v^.R;

v^.R :=v^.R^.L;

end;

dispose(P);

end;

Delete := Tree

end;

{C++}

BinTree * Delete(BinTree *Tree, BT x)

{ BinTree* P, *v;

if (!Tree) cout << "такого элемента в дереве нет!" << endl;

else if (x < Tree->inf) Tree->L = Delete(Tree->L, x);

else if (x > Tree-> inf) Tree->R = Delete(Tree->R, x);

else {P = Tree;

if (!Tree->R) Tree = Tree->L; // случай 1

else if (!Tree->L) Tree = Tree->R; // случай 1

else { v = Tree->L;

while (v->R->R) v = v->R; // случай 2

Tree->inf = v->R->inf;

P = v->R; v->R = v->R->L;

}

free(P);

}

return Tree;

}

Примечание. Если элемент повторяется в дереве несколько раз, то удаляется только первое его вхождение.

Список литературы

Для подготовки данной работы были использованы материалы с сайта http://comp-science.narod.ru