Реферат: Описание сигналов

1. Общие сведения и понятия

1.1 Понятие сигнала

Сигнал - это информационная функция, несущая сообщение о физических свойствах, состоянии или поведении какой-либо физической системы, объекта или среды, а целью обработки сигналов в самом общем смысле можно считать извлечение определенных информационных сведений, которые отображены в этих сигналах (кратко - полезная или целевая информация) и преобразование этих сведений в форму, удобную для восприятия и дальнейшего использования.

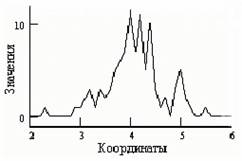
Рисунок 1.Сигнал.

1.2 Шумы и помехи

При детектировании сигналов, несущих целевую для данного вида измерений информацию, в сумме с основным сигналом одновременно регистрируются и мешающие сигналы - шумы и помехи самой различной природы (рисунок 2). К помехам относят также искажения полезных сигналов при влиянии различных дестабилизирующих факторов на процессы измерений, как, например, грозовых разрядов на электроразведочные методы измерений и т.п. Выделение полезных составляющих из общей суммы зарегистрированных сигналов или максимальное подавление шумов и помех в информационном сигнале при сохранении его полезных составляющих является одной из основных задач первичной обработки сигналов (результатов наблюдений).

Рисунок 2. Сигнал с помехами.

Следует заметить, что деление сигналов на полезные и мешающие (шумовые) является достаточно условным. Источниками мешающих сигналов также являются определенные физические процессы, явления или объекты. При выяснении природы мешающих сигналов они могут переводиться в разряд информационных.

1.3 Размерность сигналов

В общем случае сигналы являются многомерными функциями пространственных, временных и прочих независимых переменных. Все большее применение находят также многомерные сигналы, образованные некоторым множеством одномерных сигналов.

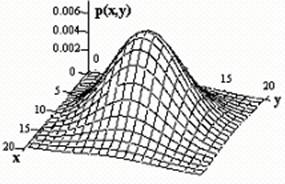
Рисунок 3. Двумерный сигнал.

Многомерные сигналы могут иметь различное представление по своим аргументам. Также многомерный сигнал может рассматриваться, как упорядоченная совокупность одномерных сигналов. С учетом этого при анализе и обработке сигналов многие принципы и практические методы обработки одномерных сигналов, математический аппарат которых развит достаточно глубоко, распространяются и на многомерные сигналы. Физическая природа сигналов для математического аппарата их обработки значения не имеет.

Вместе с тем обработка многомерных сигналов имеет свои особенности и может существенно отличаться от одномерных сигналов в силу большего числа степеней свободы. Так, при дискретизации многомерных сигналов имеет значение не только частотный спектр сигналов, но и форма растра дискретизации.

1.4 Математическое описание сигналов

Сигналы могут быть объектами теоретических исследований и практического анализа только в том случае, если указан способ их математического описания - математическая модель сигнала. Математическое описание позволяет абстрагироваться от физической природы сигнала и материальной формы его носителя, проводить классификацию сигналов, выполнять их сравнение, устанавливать степень тождества, моделировать системы обработки сигналов. Как правило, описание сигнала задается функциональной зависимостью определенного информационного параметра сигнала от независимой переменной (аргумента) – s(х), y(t) и т.п. Функции математического описания сигналов могут быть как вещественными, так и комплексными.

1.5 Математические модели сигналов

Теория анализа и обработки физических данных базируется на математических моделях соответствующих физических полей и физических процессов. Модели могут задаваться таблицами, графиками, функциональными зависимостями, уравнениями состояний и переходов из одного состояния в другое и т.п. Формализованное описание может считаться математической моделью оригинала, если оно позволяет с определенной точностью прогнозировать состояние и поведение изучаемых объектов путем формальных процедур над их описанием.

Неотъемлемой частью любой математической модели сигнала является также область определения сигнала, которая устанавливается интервалом задания независимой переменной. Примеры задания интервала для переменных:

a ≤ x ≤ b, x Î [a,b].

a < y ≤ b, y Î (a,b].

a < z < b, z Î (a,b).

Пространство значений независимой переменной от - до + обычно обозначаетcя через индекс R:=(- ,+ ), x Î R.

Кроме задания области определения сигнала могут быть также заданы виды численных значений переменных (целые, рациональные, вещественные, комплексные).

1.6 Виды моделей сигналов

При анализе физических данных используются два основных подхода к созданию математических моделей сигналов.

Первый подход оперирует с детерминированными сигналами, значения которых в любой момент времени или в произвольной точке пространства являются априорно известными или могут быть достаточно точно определены (вычислены). С математических позиций детерминированный сигнал - это сигнал, который с достаточной степенью точности можно описать явными математическими формулами или вычислительными алгоритмами.

Второй подход предполагает случайный характер сигналов, которые принимают конкретные значения с некоторой вероятностью и которые можно описать только с использованием статистических характеристик. Случайность может быть обусловлена как собственной физической природой сигналов, что характерно, например, для методов ядерной геофизики, так и вероятностным характером регистрируемых сигналов как по времени или месту их появления, так и по содержанию. С этих позиций случайный сигнал может рассматриваться как отображение случайного по своей природе процесса или физических свойств объекта (процесса), которые определяются случайными параметрами или сложным строением геологической среды, результаты измерений в которой трудно предсказуемы.

1.7 Классификация сигналов

Осуществляется на основании существенных признаков соответствующих математических моделей сигналов. Все сигналы разделяют на две крупных группы: детерминированные и случайные (рисунок 4).

Рисунок 4. Классификация сигналов.

2. Типы сигналов

2.1 Аналоговый сигнал

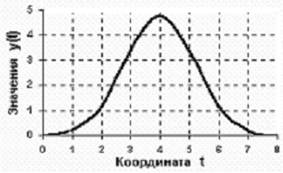
Рисунок 5. Аналоговый сигнал.

Аналоговый сигнал (analog signal) является непрерывной функцией непрерывного аргумента, т.е. определен для любого значения аргументов. Источниками аналоговых сигналов, как правило, являются физические процессы и явления, непрерывные в динамике своего развития во времени, в пространстве или по любой другой независимой переменной, при этом регистрируемый сигнал подобен (“аналогичен”) порождающему его процессу. Пример математической записи сигнала: y(t) = 4.8 exp[-(t-4)2/2.8]. Пример графического отображения данного сигнала приведен на рисунке 5, при этом как сама функция, так и ее аргументы, могут принимать любые значения в пределах некоторых интервалов y1 Δ y Δ y2, t1 Δ t Δ t2. Если интервалы значений сигнала или его независимых переменных не ограничиваются, то по умолчанию они принимаются равными от - Δ до + Δ. Множество возможных значений сигнала образует континуум - непрерывное пространство, в котором любая сигнальная точка может быть определена с точностью до бесконечности. Примеры сигналов, аналоговых по своей природе - изменение напряженности электрического, магнитного, электромагнитного поля во времени и в пространстве.

2.2 Дискретный сигнал

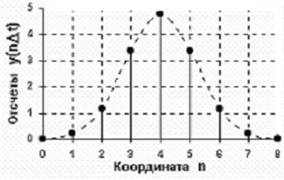
Рисунок 6. Дискретный сигнал.

Дискретный сигнал Δdiscrete signal) по своим значениям также является непрерывной функцией, но определенной только по дискретным значениям аргумента. По множеству своих значений он является конечным Δсчетным) и описывается дискретной последовательностью отсчетов Δsamples) yΔnΔt), где y1 Δ y Δ y2, Δt - интервал между отсчетами Δинтервал или шаг дискретизации, sample time), n = 0,1,2,...,N. Величина, обратная шагу дискретизации: f = 1/Δt, называется частотой дискретизации Δsampling frequency). Если дискретный сигнал получен дискретизацией Δsampling) аналогового сигнала, то он представляет собой последовательность отсчетов, значения которых в точности равны значениям исходного сигнала по координатам nΔt.

Пример дискретизации аналогового сигнала, приведенного на рисунке 5, представлен на рисунке 6. При Δt = const Δравномерная дискретизация данных) дискретный сигнал можно описывать сокращенным обозначением yΔn) или y[t]. При неравномерной дискретизации сигнала обозначения дискретных последовательностей обычно заключаются в фигурные скобки - {sΔti)}, а значения отсчетов приводятся в виде таблиц с указанием значений координат ti. Для числовых последовательностей Δравномерных и неравномерных) применяется и следующее числовое описание:

sΔti) = {a1,a2, ..., aN}, t = t1,t2, ...,tN.

2.3 Цифровой сигнал

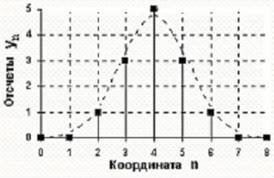Рисунок 7. Цифровой сигнал.

Цифровой сигнал Δdigital signal) квантован по своим значениям и дискретен по аргументу. Он описывается квантованной решетчатой функцией yn = Qk[yΔnΔt)], где Qk - функция квантования с числом уровней квантования k, при этом интервалы квантования могут быть как с равномерным распределением, так и с неравномерным, например - логарифмическим. Задается цифровой сигнал, как правило, в виде дискретного ряда числовых данных - числового массива по последовательным значениям аргумента при Δt = const, но в общем случае сигнал может задаваться и в виде таблицы для произвольных значений аргумента.

По существу, цифровой сигнал по своим значениям Δотсчетам) является формализованной разновидностью дискретного сигнала при округлении отсчетов последнего до определенного количества цифр, как это показано на рисунке 7. Цифровой сигнал конечен по множеству своих значений. Процесс преобразования бесконечных по значениям аналоговых отсчетов в конечное число цифровых значений называется квантованием по уровню, а возникающие при квантовании ошибки округления отсчетов Δотбрасываемые значения) – шумами Δnoise) или ошибками Δerror) квантования.

В дискретных системах и в ЭВМ сигнал всегда представлен с точностью до определенного количества разрядов, а, следовательно, всегда является цифровым. С учетом этих факторов при описании цифровых сигналов функция квантования обычно опускается Δподразумевается равномерной по умолчанию), а для описания сигналов используются правила описания дискретных сигналов. Что касается формы обращения цифровых сигналов в системах хранения, передачи и обработки, то, как правило, они представляет собой комбинации коротких одно- или двуполярных импульсов одинаковой амплитуды, которыми в двоичном коде с определенным количеством числовых разрядов кодируются числовые последовательности сигналов Δмассивов данных).

Рисунок 8. Дискретно-аналоговый сигнал.

В принципе, квантованными по своим значениям могут быть и аналоговые сигналы, зарегистрированные соответствующей аппаратурой Δрисунок 8), которые принято называть дискретно-аналоговыми. Но выделять эти сигналы в отдельный тип не имеет смысла - они остаются аналоговыми кусочно-непрерывными сигналами с шагом квантования, который определяется допустимой погрешностью измерений.

3 Преобразования типа сигналов

Операция дискретизации Δdiscretization) осуществляет преобразование аналоговых сигналов Δфункций), непрерывных по аргументу, в функции мгновенных значений сигналов по дискретному аргументу, как, например sΔt) Δ sΔnΔt), где значения sΔnΔt) представляют собой отсчеты функции sΔt) в моменты времени t = nΔt, n = 0,1,2,...N.

Операция восстановления аналогового сигнала из его дискретного представления обратна операции дискретизации и представляет, по существу, интерполяцию данных.

В общем случае, дискретизация сигналов может приводить к определенной потере информации о поведении сигналов в промежутках между отсчетами. Однако существуют условия, определенные теоремой Котельникова-Шеннона, согласно которым аналоговый сигнал с ограниченным частотным спектром может быть без потерь информации преобразован в дискретный сигнал и затем абсолютно точно восстановлен по значениям своих дискретных отсчетов.

Операция квантования или аналого-цифрового преобразования ΔАЦП; английский термин Analog-to-Digital Converter, ADC) заключается в преобразовании дискретного сигнала sΔnΔt) в цифровой сигнал sΔn) = sn » sΔnΔt), n = 0,1,2,..,N, как правило, кодированный в двоичной системе счисления. Процесс преобразования отсчетов сигнала в числа называется квантованием по уровню Δquantization), а возникающие при этом потери информации за счет округления – ошибками или шумами квантования Δquantization error, quantization noise).

При преобразовании аналогового сигнала непосредственно в цифровой сигнал операции дискретизации и квантования совмещаются.

Операция цифро-аналогового преобразования ΔЦАП; Digital-to-Analog Converter, DAC) обратна операции квантования, при этом на выходе регистрируется либо дискретно-аналоговый сигнал sΔnΔt), который имеет ступенчатую форму, либо непосредственно аналоговый сигнал sΔt), который восстанавливается из sΔnΔt), например, путем сглаживания.

Так как квантование сигналов всегда выполняется с определенной и неустранимой погрешностью Δмаксимум - до половины интервала квантования), то операции АЦП и ЦАП не являются взаимно обратными с абсолютной точностью.

4 Спектральное представление сигналов

Кроме привычного динамического представления сигналов и функций в виде зависимости их значений от определенных аргументов Δвремени, линейной или пространственной координаты и т.п.) при анализе и обработке данных широко используется математическое описание сигналов по аргументам, обратным аргументам динамического представления. Так, например, для времени обратным аргументом является частота. Возможность такого описания определяется тем, что любой сколь угодно сложный по своей форме сигнал, не имеющий разрывов первого рода, можно представить в виде суммы более простых сигналов, и, в частности, в виде суммы простейших гармонических колебаний, что выполняется при помощи преобразования Фурье. Соответственно, математически разложение сигнала на гармонические составляющие описывается функциями значений амплитуд и начальных фаз колебаний по непрерывному или дискретному аргументу – частоте изменения функций на определенных интервалах аргументов их динамического представления. Совокупность амплитуд гармонических колебаний разложения называют амплитудным спектром сигнала, а совокупность начальных фаз – фазовым спектром. Оба спектра вместе образуют полный частотный спектр сигнала, который по точности математического представления тождественен динамической форме описания сигнала.

Линейные системы преобразования сигналов описываются дифференциальными уравнениями, причем для них верен принцип суперпозиции, согласно которому реакция систем на сложный сигнал, состоящий из суммы простых сигналов, равна сумме реакций от каждого составляющего сигнала в отдельности. Это позволяет при известной реакции системы на гармоническое колебание с определенной частотой определить реакцию системы на любой сложный сигнал, разложив его в ряд гармоник по частотному спектру сигнала

Одной из основных тенденций развития сетевых технологий является передача в одной сети как дискретных, так и аналоговых по своей природе данных. Источниками дискретных данных являются компьютеры и другие вычислительные устройства, а источниками аналоговых данных являются такие устройства, как телефоны, видеокамеры, звуко- и видеовоспроизводящая аппаратура. На ранних этапах решения этой проблемы в территориальных сетях все типы данных передавались в аналоговой форме, при этом дискретные по своему характеру компьютерные данные преобразовывались в аналоговую форму с помощью модемов.

Однако по мере развития техники съема и передачи аналоговых данных выяснилось, что передача их в аналоговой форме не позволяет улучшить качество принятых на другом конце линии данных, если они существенно исказились при передаче. Сам аналоговый сигнал не дает никаких указаний ни о том, что произошло искажение, ни о том, как его исправить, поскольку форма сигнала может быть любой, в том числе и такой, которую зафиксировал приемник. Улучшение же качества линий, особенно территориальных, требует огромных усилий и капиталовложений. Поэтому на смену аналоговой технике записи и передачи звука и изображения пришла цифровая техника. Эта техника использует так называемую дискретную модуляцию исходных непрерывных во времени аналоговых процессов.

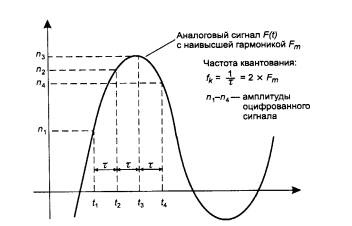
Рис. 2.19. Дискретная модуляция непрерывного процесса

Дискретные способы модуляции основаны на дискретизации непрерывных процессов как по амплитуде, так и по времени Δрис. 2.19). Рассмотрим принципы искретной модуляции на примере импулъсно-кодовой модуляции, ИКМ ΔPulse Amplitude Modulation, РАМ), которая широко применяется в цифровой телефонии.

Амплитуда исходной непрерывной функции измеряется с заданным периодом - за счет этого происходит дискретизация по времени. Затем каждый замер представляется в виде двоичного числа определенной разрядности, что означает дискретизацию по значениям функции - непрерывное множество возможных значений амплитуды заменяется дискретным множеством ее значений. Устройство, которое выполняет подобную функцию, называется аналого-цифровым преобразователем ΔАЦП). После этого замеры передаются по каналам связи в виде последовательности единиц и нулей. При этом применяются те же методы кодирования, что и в случае передачи изначально дискретной информации, то есть, например, методы, основанные на коде B8ZS или 2В 1Q.

На приемной стороне линии коды преобразуются в исходную последовательность бит, а специальная аппаратура, называемая цифро-аналоговым преобразователем ΔЦАП), производит демодуляцию оцифрованных амплитуд непрерывного сигнала, восстанавливая исходную непрерывную функцию времени.

Дискретная модуляции основана на теории отображения Найквиста - Котельникова. В соответствии с этой теорией, аналоговая непрерывная функция, переданная в виде последовательности ее дискретных по времени значений, может быть точно восстановлена, если частота дискретизации была в два или более раз выше, чем частота самой высокой гармоники спектра исходной функции.

Если это условие не соблюдается, то восстановленная функция будет существенно отличаться от исходной.

Преимуществом цифровых методов записи, воспроизведения и передачи аналоговой информации является возможность контроля достоверности считанных с носителя или полученных по линии связи данных. Для этого можно применять те же методы, которые применяются для компьютерных данных Δи рассматриваются более подробно далее), - вычисление контрольной суммы, повторная передача искаженных кадров, применение самокорректирующихся кодов.

Для качественной передачи голоса в методе ИКМ используется частота квантования амплитуды звуковых колебаний в 8000 Гц. Это связано с тем, что в аналоговой телефонии для передачи голоса был выбран диапазон от 300 до 3400 Гц, который достаточно качественно передает все основные гармоники собеседников. В соответствии с теоремой Найквиста - Котельникова для качественной передачи голоса достаточно выбрать частоту дискретизации, в два раза превышающую самую высокую гармонику непрерывного сигнала, то есть 2 * 3400 = 6800 Гц. Выбранная в действительности частота дискретизации 8000 Гц обеспечивает н екоторый запас качества. В методе ИКМ обычно используется 7 или 8 бит кода для представления амплитуды одного замера. Соответственно это дает 127 или 256 градаций звукового сигнала, что оказывается вполне достаточным для качественной передачи голоса.

При использовании метода ИКМ для передачи одного голосового канала необходима пропускная способность 56 или 64 Кбит/с в зависимости от того, каким количеством бит представляется каждый замер. Если для этих целей используется 7 бит, то при частоте передачи замеров в 8000 Гц получаем:

8000 * 7 = 56000 бит/с или 56 Кбит/с;

а для случая 8-ми бит:

8000 * 8 = 64000 бит/с или 64 Кбит/с.

Стандартным является цифровой канал 64 Кбит/с, который также называется элементарным каналом цифровых телефонных сетей.

Передача непрерывного сигнала в дискретном виде требует от сетей жесткого соблюдения временного интервала в 125 мкс Δсоответствующего частоте дискретизации 8000 Гц) между соседними замерами, то есть требует синхронной передачи данных между узлами сети. При несоблюдении синхронности прибывающих замеров исходный сигнал восстанавливается неверно, что приводит к искажению голоса, изображения или другой мультимедийной информации, передаваемой по цифровым сетям. Так, искажение синхронизации в 10 мс может привести к эффекту «эха», а сдвиги между замерами в 200 мс приводят к потере распознаваемости произносимых слов. В то же время потеря одного замера при соблюдении синхронности между остальными замерами практически не сказывается на воспроизводимом звуке. Это происходит за счет сглаживающих устройств в цифро-аналоговых преобразователях, которые основаны на свойстве инерционности любого физического сигнала - амплитуда звуковых колебаний не может мгновенно измениться на большую величину.

На качество сигнала после ЦАП влияет не только синхронность поступления на его вход замеров, но и погрешность дискретизации амплитуд этих замеров. В теореме Найквиста - Котельникова предполагается, что амплитуды функции измеряются точно, в то же время использование для их хранения двоичных чисел с ограниченной разрядностью несколько искажает эти амплитуды. Соответственно искажается восстановленный непрерывный сигнал, что называется шумом дискретизации Δпо амплитуде).

Существуют и другие методы дискретной модуляции, позволяющие представить замеры голоса в более компактной форме, например в виде последовательности 4-битных или 2-битных чисел. При этом один голосовой канал требует меньшей пропускной способности, например 32 Кбит/с, 16 Кбит/с или еще меньше. С 1985 года применяется стандарт CCITT кодирования голоса, называемый Adaptive Differential Pulse Code Modulation ΔADPCM). Коды ADPCM основаны на нахождении разностей между последовательными замерами голоса, которые затем и передаются по сети. В коде ADPCM для хранения одной разности используются 4 бит и голос передается со скоростью 32 Кбит/с. Более современный метод, Linear Predictive Coding ΔLPC), делает замеры исходной функции более редко, но использует методы прогнозирования направления изменения амплитуды сигнала. При помощи этого метода можно понизить скорость передачи голоса до 9600 бит/с.

Представленные в цифровой форме непрерывные данные легко можно передать через компьютерную сеть. Для этого достаточно поместить несколько замеров в кадр какой-нибудь стандартной сетевой технологии, снабдить кадр правильным адресом назначения и отправить адресату. Адресат должен извлечь из кадра замеры и подать их с частотой квантования Δдля голоса - с частотой 8000 Гц) на цифро-аналоговый преобразователь. По мере поступления следующих кадров с замерами голоса операция должна повториться. Если кадры будут прибывать достаточно синхронно, то качество голоса может быть достаточно высоким. Однако, как мы уже знаем, кадры в компьютерных сетях могут задерживаться как в конечных узлах Δпри ожидании доступа к разделяемой среде), так и в промежуточных коммуникационных устройствах - мостах, коммутаторах и маршрутизаторах. Поэтому качество голоса при передаче в цифровой форме через компьютерные сети обычно бывает невысоким. Для качественной передачи оцифрованных непрерывных сигналов - голоса, изображения - сегодня используют специальные цифровые сети, такие как ISDN, ATM, и сети цифрового телевидения. Тем не менее для передачи внутрикорпоративных телефонных разговоров сегодня характерны сети frame relay, задержки передачи кадров которых укладываются в допустимые пределы