
Рефераты по авиации и космонавтике
Рефераты по административному праву
Рефераты по безопасности жизнедеятельности
Рефераты по арбитражному процессу
Рефераты по архитектуре
Рефераты по астрономии
Рефераты по банковскому делу
Рефераты по сексологии
Рефераты по информатике программированию
Рефераты по биологии
Рефераты по экономике
Рефераты по москвоведению
Рефераты по экологии
Краткое содержание произведений
Рефераты по физкультуре и спорту
Топики по английскому языку
Рефераты по математике
Рефераты по музыке
Остальные рефераты
Рефераты по биржевому делу
Рефераты по ботанике и сельскому хозяйству
Рефераты по бухгалтерскому учету и аудиту
Рефераты по валютным отношениям
Рефераты по ветеринарии
Рефераты для военной кафедры
Рефераты по географии
Рефераты по геодезии
Рефераты по геологии
Рефераты по геополитике
Рефераты по государству и праву
Рефераты по гражданскому праву и процессу
Рефераты по кредитованию
Рефераты по естествознанию
Рефераты по истории техники
Рефераты по журналистике
Рефераты по зоологии
Рефераты по инвестициям
Рефераты по информатике
Исторические личности
Рефераты по кибернетике
Рефераты по коммуникации и связи
Рефераты по косметологии
Рефераты по криминалистике
Рефераты по криминологии
Рефераты по науке и технике
Рефераты по кулинарии
Рефераты по культурологии
Учебное пособие: Топогеодезична прив’язка силами і засобами артилерійських підрозділів
Учебное пособие: Топогеодезична прив’язка силами і засобами артилерійських підрозділів
1. Склад, задачі, обов’язки особового складу та приладне обладнання груп самоприв’язки артилерійських підрозділів
1.1 Склад і задачі груп самоприв’язки
Для проведення топогеодезичної прив’язки вогневих позицій і спостережних пунктів у батареях створюються групи самоприв’язки.
Група самоприв’язки вогневої позиції очолюється, як правило, командиром другого вогневого взводу; вона включає в себе двох солдат зі складу гарматних обслуг.
Група самоприв’язки спостережного пункту очолюється командиром взводу управління або командиром відділення розвідки; вона включає в себе двох солдат зі складу відділення розвідки батареї.
Особовий склад групи самоприв’язки зобов’язаний:
- здійснювати топогеодезичну прив’язки вогневої позиції або спостережного пункту по карті (аерознімку) за допомогою приладів;
- знати зміст топогеодезичної прив’язки ВП і СП та вимоги до точності її проведення;
- мати навички у швидкому орієнтуванні на місцевості за допомогою топографічної карти.
1.2 Приладне обладнання груп самоприв’язки
Для виконання топогеодезичних робіт група самоприв’язки може використовувати наступні прилади:
- перископічну артилерійську бусоль ПАБ-2А;
- артилерійський компас;
- двометрову далекомірну рейку з електроосвітленням;
- мірну стрічку для вимірювання відстаней;
- бінокль;
- номограма інструментального ходу (НИХ);
- хордокутомір з циркулем-вимірювачем;
- артилерійський круг АК-3 з МПЛ-50;
- курвіметр;
- артилерійську логарифмічну лінійку (АЛЛ);
- обчислювач топографічний модернізований (СТМ);
- електронні обчислювальні машини (ЕОМ);
- топографічні карти 1:50 000, 1:25 000;
- спеціальні карти 1:100 000 з вдрукованими координатами;
- прилад управління вогнем (планшет).
Крім того, група самоприв’язки спостережного пункту у ряді випадків для прив’язки може використовувати далекомір ДС-1, ДАК-2.
1.3 Розподіл обов’язків особового складу групи при виконанні топогеодезичної прив’язки
Обов’язки особового складу групи при виконанні топогеодезичної прив’язки розподіляються наступним чином.
Начальник групи ставить задачу, керує роботою особового складу групи, контролює польові і вимірювальні роботи і при необхідності особисто працює на приладі.
Перший номер (обчислювач), навчений виконанню обчислень за матеріалами польових вимірювань, в ході топогеодезичної прив’язки ВП (СП) працює на приладі (бусолі, далекомірі), веде запис спостережень і абрис, виконує обчислення і графічні роботи на карті.
Другий номер виставляє рейку на точках за вказівкою начальника групи або першого номера; закріплює на місцевості точки, що прив’язуються кілками; приймає участь у вимірюванні відстаней.
1.4 Порядок постановки задачі начальником групи
– напрямок на північ (або іншу сторону горизонту) по будь-якому предметові;
– місцезнаходження відносно найближчого орієнтира, що чітко виділяється серед інших (від загального до часткового);
– умовне найменування місцевих предметів, орієнтирів;
– положення противника;
– положення своїх військ;
– задачі групи самоприв’язки;
– рішення:
- місце основної гармати;
- дирекційний кут основного напрямку стрільби;
- точку стояння бусолі СОБ;
- точки наводки і орієнтирні точки;
- способи визначення координат і дирекційних кутів;
- початкові контурні точки;
- час закінчення робіт;
- порядок і місце подання результатів прив’язки.
2. Початкові напрямки і кути, що застосовуються в артилерії та взаємозв’язок між ними
![]() ; (2.1)
; (2.1)
![]() ; (2.2)
; (2.2)
![]() ; (2.3)
; (2.3)
![]() ; (2.4)
; (2.4)
![]() ; (2.5)
; (2.5)
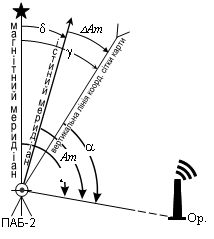
де: А – істиний азимут;
 Am –
магнітний
азимут;
Am –
магнітний
азимут;
a – дирекційний кут;
g – зближення меридіанів;
d – магнітне схилення;
DAm – поправка бусолі,
визначена на місцевості;
DAmК – поправка бусолі, визначена за даними
карти;
3. Визначення величини зближення меридіанів
3.1 Визначення зближення меридіанів по карті для довільної точки на карті
Величина зближення меридіанів для любої точки на карті визначається за формулою:
![]() (3.1)
(3.1)
де: ![]() – зближення меридіанів для
центра листа карти (вибирається із текстової довідки в лівому нижньому куті
карти).
– зближення меридіанів для
центра листа карти (вибирається із текстової довідки в лівому нижньому куті
карти).
![]() – поправка на
віддаленість точки по довготі від центру листа карти (вибирається з таблиці 1)
по значенню координати Х точки в км і віддалі Д в км точки від центру листа
карти.
– поправка на
віддаленість точки по довготі від центру листа карти (вибирається з таблиці 1)
по значенню координати Х точки в км і віддалі Д в км точки від центру листа
карти.
Знак «+» – якщо точка на схід від центра листа карти.
Знак «–» – якщо точка на захід від центра листа карти.
Таблиця 1. Таблиця
для визначення поправки ![]()
|
Х, км. |
Д, км. |
|||||
|
5 |
10 |
15 |
20 |
25 |
30 |
|
|
4 000 |
0–00,5 | 0–01,1 | 0–01,6 | 0–02,2 | 0–02,7 | 0–03,3 |
|
4 500 |
0–00,6 | 0–01,3 | 0–01,9 | 0–02,6 | 0–03,2 | 0–03,8 |
|
5 000 |
0–00,8 | 0–01,5 | 0–02,3 | 0–03,0 | 0–03,8 | 0–04,5 |
|
5 500 |
0–00,9 | 0–01,8 | 0–02,6 | 0–03,5 | 0–04,4 | 0–05,3 |
|
6 000 |
0–01,0 | 0–02,1 | 0–03,1 | 0–04,1 | 0–05,2 | 0–06,2 |
|
6 500 |
0–01,2 | 0–02,5 | 0–03,7 | 0–04,9 | 0–06,2 | 0–07,3 |
|
7 000 |
0–01,5 | 0–02,9 | 0–04,4 | 0–05,9 | 0–07,4 | 0–08,8 |
|
7 500 |
0–01,8 | 0–03,6 | 0–05,4 | 0–07,2 | 0–09,0 | 0–10,8 |
|
8 000 |
0–02,3 | 0–04,6 | 0–06,9 | 0–09,2 | 0–11,6 | 0–13,8 |
3.2 Обчислення величини зближення меридіанів по формулі
Величина зближення меридіанів для любої точки Землі може бути обчислена по формулі:
![]() (3.2)
(3.2)
де: ![]() – різниця довгот даної
точки і осьового меридіану, надана в кутових мінутах;
– різниця довгот даної
точки і осьового меридіану, надана в кутових мінутах;
L – довгота точки (визначається по карті);
L0 – довгота осьового меридіану зони, в якій знаходиться точка; визначається з таблиці 2 або обчислюється за формулою:
![]() ; (3.3)
; (3.3)
де N – номер зони, в якій знаходиться точка; обчислюється за формулою:
![]() ; (3.4)
; (3.4)
В-широта даної точки (визначається по карті).
Таблиця 2. Таблиця визначення довготи осьового меридіану L0
| Довгота точки у межах: | Довгота осьового меридіану | Довгота точки у межах: | Довгота осьового меридіану |
|
L |
L0 |
L |
L0 |
| 0° – 6° | 3° | 90° – 96° | 93° |
| 6° – 12° | 9° | 96° – 102° | 99° |
| 12° – 18° | 15° | 102° – 108° | 105° |
| 18° – 24° | 21° | 108° – 114° | 111° |
| 24° – 30° | 27° | 114° – 120° | 117° |
| 30° – 36° | 33° | 120° – 126° | 123° |
| 36° – 42° | 39° | 126° – 132° | 129° |
| 42° – 48° | 45° | 132° – 138° | 135° |
| 48° – 54° | 51° | 138° – 144° | 141° |
| 54° – 60° | 57° | 144° – 150° | 147° |
| 60° – 66° | 63° | 150° – 156° | 153° |
| 66° – 72° | 69° | 156° – 162° | 159° |
| 72° – 78° | 75° | 162° – 168° | 165° |
| 78° – 84° | 81° | 168° – 174° | 171° |
| 84° – 90° | 87° | 174° – 180° | 177° |
Приклад: обчислити
зближення меридіанів для точки з координатами: ![]() 51°17,1¢ пн. ш.,
51°17,1¢ пн. ш., ![]() 44°13,0¢ сх. д.
44°13,0¢ сх. д.
а) Рішення за допомогою артилерійської
логарифмічної лінійки.
1.
Використовуючи формули 3.3, 3.4 або таблицю 2, визначити довготу
осьового меридіану зони, в якій знаходиться дана точка: ![]() =45°.
=45°.
2.
Обчислити величину ![]() = 44°13,0¢ – 45° = – 0°47¢ = –47¢
= 44°13,0¢ – 45° = – 0°47¢ = –47¢
3. За допомогою артилерійської логарифмічної лінійки виконати множення згідно 2.2:
![]() = (–47¢)*sin (51°17,1¢) = – 36,6¢
= (–47¢)*sin (51°17,1¢) = – 36,6¢
для чого:
3.1.
Початок
(кінець) шкали движка поставити на значення ![]() = –47¢ по шкалі чисел NQ+1 корпусу лінійки без
урахування знаку.
= –47¢ по шкалі чисел NQ+1 корпусу лінійки без
урахування знаку.
3.2.
Візир центральною рискою поставити на округлене до мінут значення ![]() 51°17¢ по шкалі «Sin» на червоній стороні движка.
51°17¢ по шкалі «Sin» на червоній стороні движка.
3.3.
Напроти
центральної риски візиру на шкалі чисел NQ+1 корпусу лінійки
прочитати значення ![]() в мінутах (36,6).
в мінутах (36,6).
4. Перевести значення
зближення меридіанів ![]() в поділки кутоміру, для
чого:
в поділки кутоміру, для
чого:
4.1. Не збиваючи положення візиру переміщенням движка встановити під центральну риску візира значення 3,6 по шкалі чисел N движка.
4.2.
Напроти початку (кінця) шкали движка по шкалі чисел NQ+1 корпусу лінійки прочитати
значення зближення
меридіанів![]() у поділках кутоміру (0–10,15 »
0–10,2).
у поділках кутоміру (0–10,15 »
0–10,2).
Для точок з північною
широтою зближення меридіанів![]() має той же знак, що і
значення
має той же знак, що і
значення ![]() .
.
Відповідь: ![]() – 36,6¢ = – 0–10,2.
– 36,6¢ = – 0–10,2.
б) Рішення за допомогою таблиці 3.
1. Використовуючи
формули 3.3, 3.4 або таблицю 2, визначити довготу осьового меридіану зони, в
якій знаходиться дана точка: ![]() =45°.
=45°.
2. Обчислити
величину ![]() = 44°13,0¢ – 45° = – 0°47¢ = –47¢
= 44°13,0¢ – 45° = – 0°47¢ = –47¢
3. По значенню широти ![]() 51°17,1¢ пн. ш. та
значенню
51°17,1¢ пн. ш. та
значенню ![]() = – 47¢ по таблиці 3
визначити
= – 47¢ по таблиці 3
визначити ![]() – 0–10,2 маючи на увазі, що для точок з
північною широтою зближення меридіанів
– 0–10,2 маючи на увазі, що для точок з
північною широтою зближення меридіанів![]() має той же знак, що і
значення
має той же знак, що і
значення ![]() .
.
Відповідь: ![]() – 0–10,2.
– 0–10,2.
3.3 Визначення зближення меридіанів по графіку
Вхідними даними для визначення зближення меридіанів по графіку є повні прямокутні координати точки, для якої визначається g, округлені:
Х – до десятків кілометрів;
Y – до кілометрів (без номера зони).
Приклад: Визначити зближення меридіанів по графіку для точки з координатами: Х=75 00 180, Y= 3 423 980.
1. Визначити вхідні дані:
Х=7 500 км.
Y=424 км
2. По вхідним величинам увійти в графік, точку перехрестя винести вліво і прочитати значення g = – 1°40¢ (g = – 0–28)
4. Визначення величини магнітного схилення та оцінка магнітометричного стану місцевості
4.1 Визначення величини магнітного схилення
Величина магнітного схилення року визначення обчислюється по даним карти за формулою:
![]() , (4.1)
, (4.1)
де: ![]() – магнітне схилення
поточного року;
– магнітне схилення
поточного року;
![]() – магнітне
схилення року видання карти (вказується в текстовій довідці у лівому нижньому
куті карти);
– магнітне
схилення року видання карти (вказується в текстовій довідці у лівому нижньому
куті карти);
![]() – річна зміна
магнітного схилення в кутових хвилинах (вказується в текстовій довідці у лівому
нижньому куті карти, західна – має знак «– «, східна – має знак «+»);
– річна зміна
магнітного схилення в кутових хвилинах (вказується в текстовій довідці у лівому
нижньому куті карти, західна – має знак «– «, східна – має знак «+»);
![]() – кількість
років, що минули від року видання карти до поточного року.
– кількість
років, що минули від року видання карти до поточного року.
4.2 Оцінка магнітометричного стану місцевості
Оцінка магнітометричного стану місцевості проводиться з метою встановлення можливості застосування магнітної стрілки бусолі для визначення дирекційних кутів орієнтирних напрямків у даному районі.
В якості основної
характеристики магнітометричного стану місцевості приймається максимальне
значення градієнта магнітного схилення ![]() ,
яке визначається по ізогонам – лініям однакового магнітного схилення, що
зображаються на картах масштабу 1:1 000 000 та 1:500 000 пунктирними лініями
малинового кольору або порівнянням магнітних схилень двох суміжних карт
крупного масштабу.
,
яке визначається по ізогонам – лініям однакового магнітного схилення, що
зображаються на картах масштабу 1:1 000 000 та 1:500 000 пунктирними лініями
малинового кольору або порівнянням магнітних схилень двох суміжних карт
крупного масштабу.
а) Визначення ![]() по карті масштабу 1:1 000
000 або 1:500 000.
по карті масштабу 1:1 000
000 або 1:500 000.
1.
 Нанести на карту межі
району, магнітометричний стан якого оцінюється (мал. 1).
Нанести на карту межі
району, магнітометричний стан якого оцінюється (мал. 1).
2. Виміряти найкоротшу відстань Sкм (через позначений район) між сусідніми ізогонами, значення магнітного схилення яких відрізняється на 1° (0–17).
3. Обчислити максимальне значення градієнта магнітного схилення за формулою:
![]() . (4.2)
. (4.2)
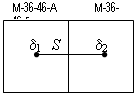
б) Визначення ![]() по двом суміжним листам
карт.
по двом суміжним листам
карт.
1.
Визначити для поточного року величини магнітного схилення ![]() і
і![]() для кожного листа карти по
формулі 4.1.
для кожного листа карти по
формулі 4.1.
2. Виміряти відстань між центрами листів карт Sкм.
3. Обчислити максимальне значення градієнта магнітного схилення за формулою:
![]() . (4.3)
. (4.3)
 Якщо обчислене
максимальне значення градієнта магнітного схилення перевищує допустиме значення
– 0–10 на 10 км., – то використовувати магнітну стрілку для
визначення дирекційних кутів не дозволяється.
Якщо обчислене
максимальне значення градієнта магнітного схилення перевищує допустиме значення
– 0–10 на 10 км., – то використовувати магнітну стрілку для
визначення дирекційних кутів не дозволяється.
В районах площинних аномалій та точкових аномалій (позначаються на картах масштабу 1:1 000 000 або 1:500 000 малиновою штриховкою і крапками малинового кольору відповідно) використання магнітної стрілки для визначення дирекційних кутів також не дозволяється.
Через значний вплив магнітних збурень на значення магнітного схилення не можна визначати дирекційний кут за допомогою магнітної стрілки бусолі і в районах, географічна широта яких перевищує 65°.
5. Визначення та уточнення поправки бусолі
5.1 Визначення поправки бусолі на місцевості
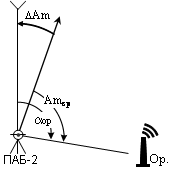 Поправку бусолі
на місцевості визначають шляхом порівняння відомого диреційного кута з магнітним
азимутом одного і того ж орієнтирного напрямку.
Поправку бусолі
на місцевості визначають шляхом порівняння відомого диреційного кута з магнітним
азимутом одного і того ж орієнтирного напрямку.
Дирекційний кут орієнтирного напрямку визначають геодезичним, гіроскопічним або астрономічним способом.
Порядок визначення:
1. Установити ПАБ-2 над точкою, з якої визначено дирекційний кут по віддаленому орієнтиру одним з вищеперелічених способів.
2. Виміряти 5 разів значення магнітного азимута по цьому орієнтиру; після кожного вимірювання збивати положення магнітної стрілки обертанням маховика установочного черв’яка.
3. Обчислити середнє значення магнітного азимута:
![]()
4. Обчислити поправку бусолі по формулі:
![]() . (5.1)
. (5.1)
 За даними
визначення поправки бусолі заповнюють бірку, яку вкладають у футляр бусолі і
використовують (в неаномалійних районах) для визначення дирекційних кутів
орієнтирних напрямків у радіусі 10 км від точки її визначення.
За даними
визначення поправки бусолі заповнюють бірку, яку вкладають у футляр бусолі і
використовують (в неаномалійних районах) для визначення дирекційних кутів
орієнтирних напрямків у радіусі 10 км від точки її визначення.
5.2 Звірка бусолей у дивізіоні
При переміщення на відстань більш ніж 10 км поправку бусолі необхідно визначити знову. За відсутності часу або неможливості визначити поправку всіх бусолей дивізіону у новому районі, можна визначити поправку для контрольної бусолі дивізіону (підручної батареї) з послідуючим виправленням поправок усіх бусолей шляхом урахування в їх поправку величини зміни поправки контрольної бусолі у новому районі.
Величина зміни поправки контрольної бусолі у новому районі обчислюється по формулі:
![]() , (5.2)
, (5.2)
де: ![]() – величина зміни поправки
контрольної бусолі у новому районі;
– величина зміни поправки
контрольної бусолі у новому районі;
![]() – значення
поправки контрольної бусолі в новому районі;
– значення
поправки контрольної бусолі в новому районі;
![]() – значення
поправки контрольної бусолі в старому районі.
– значення
поправки контрольної бусолі в старому районі.
Величина ![]() додається зі своїм знаком
до значення поправок решти бусолей дивізіону.
додається зі своїм знаком
до значення поправок решти бусолей дивізіону.
5.3 Уточнення поправки бусолі при переміщенні
Якщо в новому
районі неможливо визначити поправку бусолі ![]() ,
то дозволяється, як виняток, в радіусі 30 км користуватися старою
поправкою
,
то дозволяється, як виняток, в радіусі 30 км користуватися старою
поправкою ![]() після уведення в неї
поправку на зміну зближення меридіанів
після уведення в неї
поправку на зміну зближення меридіанів ![]() :
:
![]() . (5.3)
. (5.3)
Поправка![]() вибирається з таблиці 1 по
значенню абсциси Х точки в км і віддалі Д в км по довготі від нового району до
району визначення поправки бусолі (визначається як різниця ординат Y нового і старого
районів: Дкм = Yн – Yс).
вибирається з таблиці 1 по
значенню абсциси Х точки в км і віддалі Д в км по довготі від нового району до
району визначення поправки бусолі (визначається як різниця ординат Y нового і старого
районів: Дкм = Yн – Yс).
![]() має знак «+»,
якщо новий район східніше старого району.
має знак «+»,
якщо новий район східніше старого району.
![]() має знак «–»,
якщо новий район західніше старого району.
має знак «–»,
якщо новий район західніше старого району.
Під час проведення топогеодезичних робіт після переміщення в суміжну зону поправка бусолі повинна бути визначена в цій зоні на місцевості. У випадку, коли нема можливості визначити поправку бусолі на місцевості, вона може бути уточнена по формулі:
захід ® схід
![]() , (5.4)
, (5.4)
захід ¬ схід
де: ![]() – поправка на
зміну зближення меридіанів, визначається з таблиці 1, взята по модулю;
– поправка на
зміну зближення меридіанів, визначається з таблиці 1, взята по модулю;
![]() – поправка на перехід із
зони в зону, вибирається по значенню абсциси Х в км старого району з таблиці 4,
взята по модулю.
– поправка на перехід із
зони в зону, вибирається по значенню абсциси Х в км старого району з таблиці 4,
взята по модулю.
У формулі 5.4 верхні знаки – при переході із заходу на схід, нижні знаки – при переході зі сходу на захід. Таблиця 4.
Таблиця для визначення
поправки![]() до диреційного кута за
перехід в суміжну зону
до диреційного кута за
перехід в суміжну зону
|
хб |
Da |
хб |
Da | ||||
| градуси | D 10 км |
поділки кутоміра |
градуси | D 10 км |
поділки кутоміра |
||
| 2 000 | 1°51,7¢ | 0,54¢ | 0–31 | 5 000 | 4°15,1¢ | 0,39¢ | 0–71 |
| 2 100 | 1 57,1 | 0,53 | 0–33 | 5 100 | 4 19,0 | 0,39 | 0–72 |
| 2 200 | 2 02,4 | 0,53 | 0–34 | 5 200 | 4 22,9 | 0,39 | 0–73 |
| 2 300 | 2 07,7 | 0,53 | 0–35 | 5 300 | 4 26,8 | 0,37 | 0–74 |
| 2 400 | 2 13,0 | 0,53 | 0–37 | 5 400 | 4 30,5 | 0,37 | 0–75 |
| 2 500 | 2 18,3 | 0,52 | 0–38 | 5 500 | 4 34,2 | 0,37 | 0–76 |
| 2 600 | 2 23,5 | 0,52 | 0–40 | 5 600 | 4 37,9 | 0,35 | 0–77 |
| 2 700 | 2 28,7 | 0,51 | 0–41 | 5 700 | 4 41,4 | 0,35 | 0–78 |
| 2 800 | 2 33,8 | 0,51 | 0–43 | 5 800 | 4 44,9 | 0,34 | 0–79 |
| 2 900 | 2 38,9 | 0,51 | 0–44 | 5 900 | 4 48,3 | 0,34 | 0–80 |
| 3 000 | 2 44,0 | 0,50 | 0–46 | 6 000 | 4 51,7 | 0,32 | 0–81 |
| 3 100 | 2 49,0 | 0,50 | 0–47 | 6 100 | 4 54,9 | 0,32 | 0–82 |
| 3 200 | 2 54,0 | 0,49 | 0–48 | 6 200 | 4 58,1 | 0,32 | 0–83 |
| 3 300 | 2 58,9 | 0,49 | 0–50 | 6 300 | 5 01,3 | 0,30 | 0–84 |
| 3 400 | 3 03,8 | 0,49 | 0–51 | 6 400 | 5 04,3 | 0,30 | 0–85 |
| 3 500 | 3 08,7 | 0,48 | 0–52 | 6 500 | 5 07,3 | 0,29 | 0–85 |
| 3 600 | 3 13,5 | 0,47 | 0–54 | 6 600 | 5 10,2 | 0,28 | 0–86 |
| 3 700 | 3 18,2 | 0,47 | 0–55 | 6 700 | 5 13,0 | 0,28 | 0–87 |
| 3 800 | 3 22,9 | 0,47 | 0–56 | 6 800 | 5 15,8 | 0,26 | 0–88 |
| 3 900 | 3 27,6 | 0,46 | 0–58 | 6 900 | 5 18,4 | 0,26 | 0–88 |
| 4 000 | 3 32,2 | 0,45 | 0–59 | 7 000 | 5 21,0 | 0,25 | 0–89 |
| 4 100 | 3 36,7 | 0,45 | 0–60 | 7 100 | 5 23,5 | 0,25 | 0–90 |
| 4 200 | 3 41,2 | 0,45 | 0–61 | 7 200 | 5 26,0 | 0,23 | 0–91 |
| 4 300 | 3 45,7 | 0,44 | 0–63 | 7 300 | 5 28,3 | 0,23 | 0–91 |
| 4 400 | 3 50,1 | 0,43 | 0–64 | 7 400 | 5 30,6 | 0,22 | 0–92 |
| 4 500 | 3 54,4 | 0,42 | 0–65 | 7 500 | 5 32,8 | 0,21 | 0–92 |
| 4 600 | 3 58,6 | 0,42 | 0–66 | 7 600 | 5 34,9 | 0,20 | 0–93 |
| 4 700 | 4 02,8 | 0,42 | 0–67 | 7 700 | 5 36,9 | 0,20 | 0–94 |
| 4 800 | 4 07,0 | 0,41 | 0–69 | 7 800 | 5 38,9 | 0,20 | 0–94 |
| 4 900 | 4 11,1 | 0,40 | 0–70 | 7 900 | 5 40,7 | 0,18 | 0–95 |
5.4 Визначення поправки бусолі за даними карти
Поправка бусолі
за даними карти -![]() визначається по
формулі:
визначається по
формулі:
![]() , (5.5)
, (5.5)
де: g – зближення меридіанів для даної точки, визначається по формулам 3.1, 3.2 або по графіку;
![]() – магнітне
схилення поточного року; визначається по формулі 4.1.
– магнітне
схилення поточного року; визначається по формулі 4.1.
Поправка бусолі, що визначена за даними карти, не може використовуватися для визначення дирекційних кутів орієнтирних напрямків, бо вона не враховує інструментальну поправку D, тобто:
![]() . (5.6)
. (5.6)
Інструментальна поправка D може бути визначена як різниця поправки бусолі, визначеної на місцевості по формулі 5.1 і визначеної за даними карти по формулі 5.5 для однієї і тієї ж точки:
![]() , (5.7)
, (5.7)
а потім у новому районі додається зі своїм знаком до поправки бусолі, визначеної за даними карти за формулою 5.5.
6. Основні елементи геодезичних обчислень
Основними елементами обчислень є:
– перехід від дирекційного кута одного напрямку до дирекційного кута другого напрямку, що визначається з цієї ж точки;
– визначення величини горизонтального кута по дирекційним кутам напрямків, що утворюють цей кут;
– рішення прямої та оберненої геодезичної задачі на площині;
– вирішення трикутника;
– визначення величини зближення меридіанів;
– перехід від істинного або магнітного азимуту до дирекційного кута;
– визначення висот точок.
6.1 Перехід від дирекційного кута одного напрямку до дирекційного кута другого напрямку, що визначається з цієї ж точки.
Дирекційний кут напрямку, що визначається дорівнює дирекційному куту відомого (вихідного) напрямку плюс горизонтальний кут, відрахований за годинниковою стрілкою від відомого напрямку до напрямку, що визначається:
(АВ) = (АС) + Ð1
Якщо отриманий дирекційний кут перевищує 360° (60–00), то його зменшують на цю величину.
Горизонтальний кут дорівнює різниці дирекційних кутів правого та лівого напрямків, що складають кут:
Ð1 = (АВ) – (АС);
Ð2 = (АС) – (АВ).
Якщо при обчисленні горизонтального кута дирекційний кут, що віднімається перевищує зменшуваний дирекційний кут, то до останнього додають 360° (60–00).6.2. Вирішення прямої геодезичної задачі на площині.
Вирішення прямої геодезичної задачі (ПГЗ) на площині полягає у обчисленні координат точки, що визначається по відомим координатам заданої точки, відстані між ними та дирекційному куту з заданої точки на точку, що визначається.
ПГЗ вирішують у такій послідовності:
1. Обчислюють прирощення координат DХ та DY за формулами:
DХ = АВ cos a;
DY = АВ sin a.
2. Визначають координати точки В за формулами:
XB=XA+DХ;
YB=YA+DY.
Для математичного запису прямої геодезичної задачі підставимо формули 1 у формули 2:
XB=XA+АВ cos a;
YB=YA+АВ sin a.
а) обчислення прямої геодезичної задачі за допомогою артилерійської логарифмічної лінійки (АЛЛ).
Так як лінійка має шкалу синусів тільки від 0 до 15–00, при обчисленні прирощень ΔХ і ΔY для рішення ПГЗ, яка може бути вирішена тоді, коли дирекційний кут знаходиться у 1-й чверті і має значення від 0–00 до 15–00 необхідно ввести поняття румба.
Румб – це гострий кут, створений віссю Х і напрямком на визначаєму точку (орієнтир, ціль). У залежності від розміщення визначаємої точки відносно заданої, напрямок між ними може знаходитись у різних четвертях.
Для рішення ПГЗ у другій, третій і четвертій четвертях необхідно від дирекційного кута напрямку з заданої точки на визначаєму перейти до гострого кута R (румб) у першій четверті. (див. малюнок)
Приклад. Визначити прямокутні координати цілі 202, якщо з СП з координатами Х=77810, Y=13315 виміряні: α=48–65, Дц=3250
Порядок рішення:
1. Визначити значення R i (15–00 – R). R=11–35, (15–00-R)=3–65
2. По дирекційному куту aц визначити четверть i знаки прирощення координат (в IV чв.: «+» ΔХ; « – «ΔY)
3. Обчислити значення прирощення координат ΔХ, ΔY:
а) ΔХ = Д * sin (15 – R), для чого початок (кінець) движку встановлюють на значення дальності Д по шкалі чисел лінійки NQ+1. Візир центр. рискою встановлюють на значення кута (15-R) по шкалі S або SіТ і по рисці візира на шкалі чисел лінійки NQ+1 читають значення: ΔХ=+1210.
б) ΔY= sin R, для чого не збиваючи положення движка (при необхідності – перемістити движок на значення Д іншим кінцем шкали), встановлюють візир центральною рискою на значення кута R по шкалі S або SіТ, і під рискою візира на шкалі чисел лінійки NQ+1 читають значення ΔY=-3010.
Примітка: для визначення порядка числа значень прирощення координат ΔХ і ΔY використовують правило:
– якщо кути R (15-R) визначались по шкалі Sin, то 0,1Д < |ΔУ| (чи |ΔХ|) < Д.
– якщо кути R (15-R) визн. по шкалі SіТ, то 0,01Д < |ΔУ| (чи |ΔХ|) < 0,1Д.
– якщо кути R (15-R) визн. по точках шкали SіТ, то 0,001Д < |ΔУ| (чи |ΔХ|)< 0,01Д.
4. Визначити координати цілі: Хц = Хап + ΔХ; Хц =79 020;
Yц = Усп + ΔY; Yц =10 305
б) обчислення прямої геодезичної задачі за допомогою обчислювача СТМ
Обчислення прирощень координат (частковий випадок рішення прямої геодезичної задачі) виробляється за допомогою обчислювача, користуючись допоміжною таблицею1, що нанесена на внутрішньому крузі.
Згідно цієї таблиці значення прирощень координат ΔХ та ΔY будуть отримані як результат множення відстані Д відповідно на:
– sin (15-a) і на sin (a) у першій чверті;
– sin (a-15) і на sin (30-a) у другій чверті;
– sin (45-a) і на sin (a-30) у третій чверті;
– sin (a-45) і на sin (60-a) у другій чверті.
Для виконання множення:
1) суміщають нульовий радіус рухомого круга відліком, що відповідає значенню Д;
2) встановлюють індекс движка на значення відповідного кута (згідно таблиці 1) по шкалі синусів 4 (якщо кут у межах від 0–95,7 до 15–00,0) або по шкалі синусів 5 (якщо кут у межах від 0–09,6 до 0–95,7);
3) знімають напроти індексу движка по шкалі чисел 3 відлік, що відповідає значенню прирощення координат.
Для визначення порядку прирощення координат використовують
правило:
– якщо кут у межах від 0–95,7 до 15–00,0, то: 0,1Д < |ΔУ| (чи |ΔХ|) < Д;
– якщо кут у межах від 0–09,6 до 0–95,7, то: 0,01Д < |ΔУ| (чи |ΔХ|) < 0,1Д;
– якщо кут у межах від 0–00,0 до 0–09,6, то: 0,001Д < |ΔУ| (чи |ΔХ|) < 0,01Д.
Приклад: обчислити прирощення координат, якщо дальність Д= 635 м, дирекційний кут a=28–45,5:
1) за таблицею 1 обчислюють кути (a-15) і (30-a) для визначення ΔХ і ΔУ, ці кути будуть дорівнювати відповідно 13–45,5 і 1–54,5;
2) суміщають нульовий радіус рухомого круга з відліком «635», що відповідає дальності 635 м по шкалі чисел 3;
3) встановлюють індекс движка на відлік 13–45,5 по шкалі 4 і напроти індексу по шкалі 3 знімають відлік «626», що відповідає значенню прирощення ΔХ=626 м;
4) встановлюють індекс движка на відлік 1–54,5 по шкалі 4 і напроти індексу по шкалі 3 знімають відлік «102», що відповідає значенню прирощення ΔУ=102 м.
Знаки прирощень – відповідно таблиці 1.
в) обчислення прямої геодезичної задачі за допомогою мікрокалькуляторів.
Мікрокалькулятори вітчизняних та відомих зарубіжних виробників дозволяють обчислювати прирощення координат при рішенні ПГЗ без переходу від дирекційного кута до румбу.
Рішення за допомогою інженерних калькуляторів:
1. Ввести значення дирекційного кута в поділках кутоміра, відокремивши великі поділки від малих комою.
2. Натиснути ´, 6 для переведення п.к. у градуси і долі градуса.
3. Натиснути М+.
4. Натиснути F COS.
5. Ввести дальність.
6. Натиснути ´.
7. Ввести Ха.
8. Натиснути +.
9. Зчитати на дисплеї значення координати Х визначаємої точки.
10. Натиснути MR.
11. Натиснути F SIN.
12. Ввести дальність.
13. Натиснути ´.
14. Ввести Yа.
15. Натиснути +.
16. Зчитати на дисплеї значення координати Y визначаємої точки.
При використанні вітчизняних програмуємих калькуляторів МК-61, МК-52 можливе рішення як в режимі виконання програми, так і в ручному режимі.
Рішення в режимі виконання програми прискорює процес рішення і зменшує імовірність помилки оператора при рішенні, але потребує попереднього введення (виклик з пам’яті для МК-52) відповідної програми і рішення контрольного прикладу; тому воно доцільне при виконанні великої кількості подібних задач (наприклад, визначення координат цілей, засічених з одного СП).
Програма для рішення ПГЗ:
| Крок | Дія | Код | Крок | Дія | Код | |
| 00 | В | ОЕ | 08 | F sin | 1С | |
| 01 | 6 | 06 | 09 | ´ | 12 | |
| 02 | ´ | 12 | 10 | П®х 2 | 62 | |
| 03 | х®П 3 | 43 | 11 | + | 10 | |
| 04 | F cos | 1Г | 12 | ' | 14 | |
| 05 | ´ | 12 | 13 | П®х 1 | 61 | |
| 06 | ' | 14 | 14 | + | 10 | |
| 07 | П®х 3 | 63 | 15 | с/п | 50 |
Розподіл регістрів:
R1 – ХА, R2 – УА, R3 – a.
Порядок рішення:
1. Перемикач системи кутів поставити у положення «Г» (градуси).
2. Ввести ХА у регістр R1: набрати ХА, натиснути х-П 1.
3. Ввести УА у регістр R2: набрати УА, натиснути х-П 2.
4. Ввести Д.
5. Натиснути 2 рази кнопку В.
6. Ввести a.
7. Натиснути в/о, с/п.
8. По закінченню виконання програми на дісплеї зчитати значення ХВ.
9. Натиснути ', на дисплеї зчитати значення УВ.
При повторному рішенні задачі з тими ж самими значеннями ХА і УА у відповідні регістри їх не вводити (тобто починати виконання з пункту 4), бо вони зберігаються у цих регістрах, доки не буде вимкнено живлення або оператор не змінить їх сам.
Контрольний приклад:
Ввести: 1000 х-П 1 2000 х-П 2 444 В В 33 в/о с/п.
Після закінчення виконання програми на дисплеї: 577,730906.
Натиснути ', на дисплеї: 1862,7964544.
Рішення в ручному режимі доцільне, коли машинна пам’ять використовується для зберігання програм рішення більш громіздких задач; задача буде виконуватись одноразово і оператор передбачає проведення контролю обчислень, хоча б грубо.
Порядок рішення:
1. Перемикач системи кутів поставити у положення «Г» (градуси).
2. Ввести Д.
3. Натиснути 2 рази кнопку В.
4. Ввести a.
5. Натиснути В 6 * х-П 3 F sin * ' П-х 3 F cos *.
6. Ввести XА.
7. Натиснути +, на дисплеї зчитати значення XВ.
8. Натиснути '.
9. Ввести YА.
10. Натиснути +, на дисплеї зчитати значення YВ.
Останнім часом надійшли до продажу інженерні калькулятори зарубіжного виробництва, що мають вбудовані функції переобчислення полярних координат в прямокутні і навпаки, що дозволяє безпосередньо обчислювати прирощення координат. Використання цих функцій здійснюється за допомогою клавіш a i b у поєднанні з функціональною клавішею 2ndF. Вирішення прямої геодезичної задачі за допомогою таких калькуляторів здійснюється в наступній послідовності.
1. Увімкнути калькулятор.
2. Упевнитись, що калькулятор налаштований для роботи у градусній системі (не у радіанах і не у градах), – у верхній частині індикатора виведено DEG (а не RAD і не GRAD).
3. Ввести значення дирекційного кута в поділках кутоміра, відокремивши великі поділки від малих комою.
4. Натиснути ´, 6 для переведення п.к. у градуси і долі градуса; натиснути b.
5. Ввести значення дальності, натиснути а.
6. Натиснути 2ndF, b; (на дисплеї – значення Dх); натиснути х®М.
7. Натиснути b +, ввести значення Усп, натиснути =; прочитати за дисплеї значення Уц.
8. Натиснути MR +, ввести значення Xсп, натиснути =; прочитати на дисплеї значення Xц.
6.3 Вирішення оберненої геодезичної задачі на площині
Вирішення оберненої геодезичної задачі (ОГЗ) на площині полягає у визначенні дирекційного кута a і відстані Д по відомим різницям координат двох точок ΔХ та ΔY.
Рішення ОГЗ виконують у наступній послідовності:
1. Визначають тангенс гострого кута R, утвореного віссю ОХ і напрямком АВ за формулою:
![]()
По величині ![]() знаходять кут в першій
чверті
знаходять кут в першій
чверті ![]() .
.
2. Від кута ![]() переходять до
дирекційного кута a у відповідності зі знаками прирощень Dх і Dу. (рис. хх).
переходять до
дирекційного кута a у відповідності зі знаками прирощень Dх і Dу. (рис. хх).
3. Обчислюють відстань між точками А і В за формулами:
![]() при R>45°
(7–50);
при R>45°
(7–50);
![]() при R<45°
(7–50).
при R<45°
(7–50).
а) обчислення оберненої геодезичної задачі за допомогою артилерійської логарифмічної лінійки (АЛЛ).
При аналітичному методі рішення ОГЗ на АЛЛ, визначення дирекційного кута і дальності здійснюється не через (R), а через кут ρ – гострий кут, створений вісcю Х або У і напрямком на визначаєму точку (орієнтир, ціль). Це викликано тим, що шкала тангенсів на движку АЛЛ в межах від 0–00 до 7–50. Відповідно кут (ρ) може приймати значення від 0–00 до 7–50.
Позначимо менше (за абсолютною величиною) прирощення координат через b, а більше прирощення через а.
![]() ,
, ![]()
Перехід від кута (ρ) до дирекційного кута здійснюється з використанням таблиці, яка нанесена на зворотній стороні корпуса лінійки.
Приклад: Визначити дирекційний кут і дальність до цілі, якщо:
Ц _ Х=77870 У=08895
ВП Х=73485 У=09307
ΔХ=+4385 ΔУ=–412
(а) (b)
Рішення:
1. Визначити прирощення координат ΔХ і ΔУ.
2. Визначити значення кута (ρ). Для чого візир центральною рискою встановити на значення «b» меншого прирощення по шкалі чисел (NQ+1) корпуса лінійки. Початок (кінець) шкали движка лінійки встановити на значення «а» більшого прирощення координат по шкалі чисел (NQ+1) корпуса лінійки. «ρ» Під рискою візира прочитати значення «ρ» (ρ=0–90). Примітка: значення кута «ρ» беруть:
- по шкалі тангенсів, якщо: а>b в 1–10 разів
- по шкалі «S і Т», якщо: а>b в 10–100 раз
- по точкам шкали «S і Т», якщо а>b в 100–1000 разів
3. Визначити кут (α). Для чого за таблицею (на зворотній стороні лінійки) по величинам і знакам прирощень координат ΔХ і ΔУ здійснити перехід від кута ρ до дирекційного кута (α). α = 60–00 – 0–90 = 59–10
4. Визначити дальність Д. Для чого, не збиваючи положення візира, під його центральну риску підвести движком значення кута (ρ) по шкалі sin і проти початку (кінця) шкали движка лінійки прочитати значення дальності (Д), маючи на увазі, що
![]()
5. При кутах (ρ=<0–90), дальність (Д) практично рівна значенню більшого прирощення координат. Для отримання дальності більш точно, необхідно проводити визначення дальності по значенню більшого прирощення координат (а) і куту (ρ/2).
Для визначення величини (Δа) на артилерійській логарифмічній лінійці необхідно:
Початок (кінець) шкали движка встановити на значення (b) – меншого прирощення координат по шкалі (NQ+1) корпуса лінійки.
Візир, центральною рискою встановити на значення кута по шкалі tg або «S і Т» і під рискою візира на шкалі чисел (NQ+1) прочитати значенням Δа:.Δа = 19 м; Д=4385+19=4404 м
Примітка:
а) якщо ρ/2 брався по шкалі tg, то 0,1b <Δа < b
б) якщо ρ/2 брався по шкалі «S и Т», то 0,01b <Δа < 0,1b
в) якщо ρ/2 брався по точках шкал S и Т, то 0,001b <Δа < 0,01b
б) обчислення оберненої геодезичної задачі за допомогою обчислювача СТМ
Обчислення дирекційного кута виробляють діленням меншого прирощення координат на більше по формулам таблиці 2, знімаючи відлік r зі шкали 1 або 2: якщо одне з прирощень більше другого від 1 до 10 раз, то відлік r знімають зі шкали 1, якщо одне з прирощень більше другого від 10 до 100 раз, то відлік r знімають зі шкали 2, а якщо одне з прирощень більше другого від 100 до 1000 раз, то відлік r також знімають зі шкали 2, але зменшують його в 10 разів.
Відстань Д обчислюють діленням більшого прирощення координат на синус більшого кута (r або 15-r).
Приклад: обчислити дирекційний кут a і відстань Д по відомим різницям координат ΔХ=-2448 та ΔY=+2992.
Рішення.
Для обчислення дирекційного кута a:
– встановлюють індекс движка на менше прирощення координат по шкалі 3;
– обертанням рухомого кругу встановлюють напроти індексу движка більше прирощення координат по шкалі 6;
– суміщають індекс движка з нульовим радіусом рухомого круга і напроти індексу движка на основному крузі зчитують зі шкали 1 значення r = 6–54,4;
–
в таблиці 2 в рядку зі знаками прирощень координат ![]() відшукують формулу (a=15+r), за якою обчислюють:
відшукують формулу (a=15+r), за якою обчислюють:
a=15–00 + 6–54,4 = 21–54,4
Для обчислення відстані:
– встановлюють індекс движка на більше прирощення (2992) по шкалі 3;
– обертанням рухомого круга встановлюють напроти індексу синус 15 – r (8–46,6) по шкалі 4;
– суміщують індекс движка з нульовим радіусом рухомого круга і по шкалі 3 напроти індексу движка зчитують значення Д=3865.
в) обчислення оберненої геодезичної задачі за допомогою мікрокалькуляторів МК-61, МК-52.
Програма для рішення ОГЗ для МК-52:
| Крок | Дія | Код | Крок | Дія | Код | |
| 00 | П®х 3 | 63 | 15 | 6 | 06 | |
| 01 | П®х 1 | 61 | 16 | ¸ | 13 | |
| 02 | – | 11 | 17 | П®х 9 | 69 | |
| 03 | В | OE | 18 | F x³0 | 59 | |
| 04 |
F х2 |
22 | 19 | 23 | 23 | |
|
|
П®х 4 | 64 | 20 | F | 25 | |
| 06 | П®х 2 | 62 | 21 | БП | 51 | |
| 07 | – | 11 | 22 | 28 | 28 | |
|
|
х®П 9 | 49 | 23 | F | 25 | |
| 09 |
F х2 |
2 | 24 | /–/ | OL | |
| 10 | + | 10 | 25 | 6 | 06 | |
| 11 |
F |
21 | 26 | 0 | 00 | |
| 12 | х®П d | 4Г | 27 | + | 10 | |
| 13 | ¸ | 13 | 28 | х®П а | 4– | |
| 14 |
F cos –1 |
1– | 29 | с/п | 50 |
Порядок рішення:
1.
Ввести Хвп, натиснути х®П 1, ввести Увп, натиснути
х®П 2, ввести Хц, натиснути х®П 3, ввести Уц, натиснути х®П 4.
2. Після зупинки: зчитати значення a, воно також зберігається в регістрі А.
3. Натиснути П®х d, зчитати значення Д.
Рішення ОГЗ за допомогою калькуляторів з вбудованими функціями переобчислення полярних координат у прямокутні і навпаки здійснюється у наступному порядку:
1. Увімкнути калькулятор.
2. Упевнитись, що калькулятор налаштований для роботи у градусній системі (не у радіанах і не у градах), – у верхній частині індикатора виведено DEG (а не RAD і не GRAD).
3. Ввести Хц, натиснути –, ввести Хвп, натиснути =, х®М.
4. Ввести Уц, натиснути –, ввести Увп, натиснути =.
5. Натиснути b.
6. Натиснути MR, натиснути а.
7. Натиснути 2ndF, а; на дисплеї зчитати значення Д.
8. Натиснути b, ¸, 6, =, на дисплеї зчитати значення дирекційного кута a у поділках кутоміра (великі поділки відокремлені від малих комою), при отриманні від’ємного значення – додати до нього 60: натиснути +, 6, 0, =, зчитати на дисплеї значення a.
6.4 Вирішення трикутника
Вирішення трикутника зводиться до обчислення по двом відомим кутам і відомою однією стороною третього кута – двох інших сторін, або до обчислення по відомим двом сторонам і куту між ними – третьої сторони і двох кутів.
а) Вирішення трикутника за двома кутами і однією стороною.
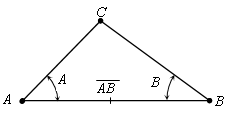 Дано: довжина
сторони
Дано: довжина
сторони ![]() і кути А і В.
Визначити кут С та довжини сторін
і кути А і В.
Визначити кут С та довжини сторін ![]() і
і
![]() .
.
В цьому випадку рішення трикутника виконують у такій послідовності.
1. Визначають кут С за формулою:
С =180° – (А + В) або С=30–00 – (А + В)
2. Визначають
довжини сторін ![]() і
і ![]() за формулами:
за формулами:
![]() ,
, ![]() .
.
В артилерійській практиці ця задача зустрічається при визначенні координат точки прямою засічкою по виміряним кутам, а також при визначенні координат цілі за допомогою спряженого спостереження.
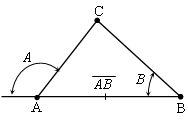 При організації
спряженого спостереження з орієнтуванням приладів на пунктах нулями вправо
схема вимірювання кутів А і В дещо відрізняється:
При організації
спряженого спостереження з орієнтуванням приладів на пунктах нулями вправо
схема вимірювання кутів А і В дещо відрізняється:
В цьому випадку кут С визначають за формулою:
С= А – В,
довжини сторін визначаються за вищенаведеними формулами.
Обчислення за допомогою АЛЛ.
Обчислити кут С.
Якщо кут А (В) перевищують 15 – 00 (90°), то, оскільки шкала синусів до 15 – 00, розраховують кут А¢ (В¢) за формулою:
А¢ = 30 – 00 – А (В¢ = 30–00 – В) і використовують його при подальших обчисленнях.
На лінійці встановлюють край шкали движка проти бази Б по шкалі чисел N корпуса лінійки. Потім, не рухаючи движка, риску візира встановлюють напроти кута В на шкалі Sin.
![]()
![]()
![]()
![]() Далі, не збиваючи
положення візира, підводять під його риску значення кута С по
шкалі Sin (SиT) і проти краю шкали движка по шкалі чисел N корпуса лінійки визначають
значення АС. Порядок відстані АС визначають
окомірно, приблизними розрахунками, або по величині
Далі, не збиваючи
положення візира, підводять під його риску значення кута С по
шкалі Sin (SиT) і проти краю шкали движка по шкалі чисел N корпуса лінійки визначають
значення АС. Порядок відстані АС визначають
окомірно, приблизними розрахунками, або по величині ![]() , маючи на увазі,
що коли кут С брався по шкалі Sin, то відстань АС
буде у межах від Б¢ до 10*Б¢, а якщо кут С
брався по шкалі SиТ, то відстань АС буде у межах від 10*Б¢ до 100*Б¢.
, маючи на увазі,
що коли кут С брався по шкалі Sin, то відстань АС
буде у межах від Б¢ до 10*Б¢, а якщо кут С
брався по шкалі SиТ, то відстань АС буде у межах від 10*Б¢ до 100*Б¢.
Обчислення за допомогою СТМ
Приклад: обчислити за допомогою СТМ відстань АС і ВС, якщо
відомі кути: А =13–74,9; В =12–83,2 і база ВА = 431 м.
1. Обчислити кут С = А–В =13–74,9 – 12–83,2 = 0–91,7.
2. Встановити індекс движка на відлік «431», що відповідає базі ВА по шкалі 3 основного круга.
3. Сумістити відлік С=0–91,7 шкали 5 рухомого круга з індексом движка.
4. Встановити індекс движка на відлік В=12–83,2 по шкалі 4 рухомого круга і напроти індексу движка по шкалі 3 зчитати відлік «348», що відповідає відстані АС = 4380 м.
5. Встановити індекс движка на відлік А=13–74,9 по шкалі 4 рухомого круга і напроти індексу движка по шкалі 3 зчитати відлік «446», що відповідає відстані ВС = 4460 м.
Обчислення за допомогою мікрокалькулятора
1. Увімкнути калькулятор.
2. Упевнитись, що калькулятор налаштований для роботи у градусній системі (не у радіанах і не у градах), – у верхній частині індикатора виведено DEG (а не RAD і не GRAD).
3. Ввести кут С у п.к., натиснути ´, 6, =, sin, х®М.
4. Ввести кут В у п.к., ´, 6, =, sin, ¸, МR, =.
5. Натиснути ´, ввести значення АВ, натиснути =, зчитати на дисплеї значення АС.
6. Ввести кут А у п.к., ´, 6, =, sin, ¸, МR, =.
7. Натиснути ´, ввести значення АВ, натиснути =, зчитати на дисплеї значення ВС.
б) Вирішення трикутника за двома сторонами і кутом між ними.
Дано: кут Р та довжини сторін АР і ВР.
Визначити кути А і В та довжину сторони АВ.
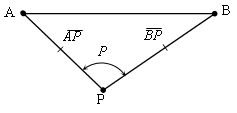 В цьому випадку
рішення трикутника виконують у такій послідовності:
В цьому випадку
рішення трикутника виконують у такій послідовності:
1. Визначають напівсуму кутів А і В за формулою:
![]()
2. Визначають
величину ![]() за формулою:
за формулою:
![]()
3. Визначають напіврізницю кутів А і В за формулою:
![]()
4. Обчислюють кути А і В за формулами:
![]() ,
, ![]()
5. Обчислюють довжину сторони АВ за формулою:
![]() , або
, або ![]()
6.5 Визначення висот точок
Абсолютні висоти точок, що прив’язуються, визначають по карті інтерполюванням окомірно відносно найближчих горизонталей. Висоти вогневих позицій, пунктів і постів артилерійської розвідки визначають по карті при крутизні схилу не більше 6°.
Якщо крутизна схилу більше за 6°, то висоту визначають за допомогою приладів (теодоліту або бусолі) від пункту геодезичної мережі або контурної точки, розташованої на схилі, крутизна якого на перевищує 6°.
При цьому висоту точки визначають за формулою:
![]() ,
,
де ![]() – висота вихідної
(контурної) точки;
– висота вихідної
(контурної) точки;
![]() – перевищення
точки, що прив’язується відносно вихідної (контурної).
– перевищення
точки, що прив’язується відносно вихідної (контурної).
Величину![]() визначають за формулою:
визначають за формулою:
![]() , або
, або ![]()
де Д – відстань між вихідною точкою і точкою, що прив’язується (визначається по карті або за допомогою далекоміра), м;
![]() – кут місця при
спостереженні з вихідної точки на точку, що прив’язується; він дорівнює куту
місця цілі з точки що прив’язується на вихідну точку, взятому з протилежним знаком:
– кут місця при
спостереженні з вихідної точки на точку, що прив’язується; він дорівнює куту
місця цілі з точки що прив’язується на вихідну точку, взятому з протилежним знаком:
![]() ,
,![]()
Першою формулою користуються при визначенні відстані Д по карті (горизонтальної дальності), а другою – при визначенні відстані ДН за допомогою далекоміра (нахиленої дальності).
Знак перевищення![]() відповідає знаку кута
місця
відповідає знаку кута
місця ![]() .
.
При проведенні
приблизних розрахунків для визначення перевищення![]() при
незначному значенні
при
незначному значенні![]() (до 1–00) можна
скористатися формулою тисячних з обов’язковим урахуванням 5%-ної поправки:
(до 1–00) можна
скористатися формулою тисячних з обов’язковим урахуванням 5%-ної поправки:
![]()
Помилка наближення при застосуванні цієї формули складе -0,1%, тобто при дальності Д » 1000 м вона буде складати до 0,1 м.
При обчисленнях за наближеною формулою при e » 2–00 помилка складе 1%, що при дальності Д»1000 м приведе до неприпустимих помилок при обчисленні абсолютної висоти визначаємої точки.