Рефераты по авиации и космонавтике
Рефераты по административному праву
Рефераты по безопасности жизнедеятельности
Рефераты по арбитражному процессу
Рефераты по архитектуре
Рефераты по астрономии
Рефераты по банковскому делу
Рефераты по сексологии
Рефераты по информатике программированию
Рефераты по биологии
Рефераты по экономике
Рефераты по москвоведению
Рефераты по экологии
Краткое содержание произведений
Рефераты по физкультуре и спорту
Топики по английскому языку
Рефераты по математике
Рефераты по музыке
Остальные рефераты
Рефераты по биржевому делу
Рефераты по ботанике и сельскому хозяйству
Рефераты по бухгалтерскому учету и аудиту
Рефераты по валютным отношениям
Рефераты по ветеринарии
Рефераты для военной кафедры
Рефераты по географии
Рефераты по геодезии
Рефераты по геологии
Рефераты по геополитике
Рефераты по государству и праву
Рефераты по гражданскому праву и процессу
Рефераты по кредитованию
Рефераты по естествознанию
Рефераты по истории техники
Рефераты по журналистике
Рефераты по зоологии
Рефераты по инвестициям
Рефераты по информатике
Исторические личности
Рефераты по кибернетике
Рефераты по коммуникации и связи
Рефераты по косметологии
Рефераты по криминалистике
Рефераты по криминологии
Рефераты по науке и технике
Рефераты по кулинарии
Рефераты по культурологии
Реферат: Устойчивость линейных систем автоматического управления
Реферат: Устойчивость линейных систем автоматического управления
Реферат
на тему:
"Устойчивость линейных систем автоматического управления"
1. Общие понятия устойчивости
Устойчивость – это свойство системы возвращаться в исходное состояние после вывода ее из состояния равновесия и прекращения действия возмущения. Устойчивость – это одно из основных требований, предъявляемых к системе. Если система не устойчива, то она не работоспособна. Рассмотрим математическое понятие устойчивости.
Движение линейной системы автоматического управления описывается линейным, неоднородным уравнением:
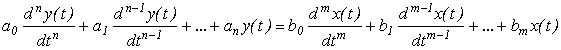
при этом правая часть – входное воздействие, а левая – реакция выхода.
Решение уравнения можно записать в виде:
![]() (1)
(1)
где ![]() - представляет собой общее
решение однородного уравнения и определяет переходный процесс;
- представляет собой общее
решение однородного уравнения и определяет переходный процесс; ![]() - представляет собой
частное решение неоднородного уравнения и определяет установившийся режим.
- представляет собой
частное решение неоднородного уравнения и определяет установившийся режим.
Общее решение однородного уравнения имеет вид:
![]() , (2)
, (2)
где: Ск
– постоянные интегрирования, которые зависят от начальных условий; ![]() - корни характеристического
уравнения:
- корни характеристического
уравнения:
![]()
Рассмотрим характер решения при различных значениях корней характеристического уравнения.
1. Если корни действительные однократные
![]()
2. Если корни действительные кратные
![]()
3. Если корни комплексно – сопряженные однократные
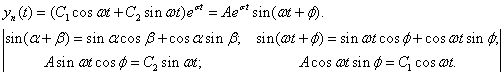
4. Пусть корни комплексно – сопряженные кратные
![]()
Для того чтобы система была устойчивой решение должно удовлетворять условию
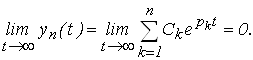 (3)
(3)
Это условие выполняется, если корни характеристического уравнения системы расположены в левой полуплоскости комплексной плоскости P.
Для устойчивости линейной системы необходимо и достаточно, чтобы корни ее характеристического уравнения располагались в левой полуплоскости комплексной плоскости P.
Характеристическое уравнение системы можно представить в виде:
![]() (4)
(4)
Если уравнение содержит хотя бы один положительный корень, то хотя бы один коэффициент характеристического уравнения будет отрицательным. Необходимое, но недостаточное условие устойчивости (при n > 2) системы – это положительность коэффициентов характеристического уравнения.
Для нахождения корней характеристического уравнения необходимо решать алгебраические уравнения. Аналитическое решение уравнений 3-го и 4-го порядка громоздки, а уравнение выше 4-го порядка не имеют аналитического решения.
В теории автоматического управления разработан ряд так называемых критериев устойчивости, которые позволяют, не решая уравнений определять устойчивость систем.
2. Критерий устойчивости Рауса-Гурвица
Для
устойчивости линейной системы необходимо и достаточно, чтобы при а0 >0
определитель Гурвица, составленный для характеристического уравнения ![]() , и все его диагональные
миноры были положительны.
, и все его диагональные
миноры были положительны.
Определитель Гурвица имеет вид:
 (5)
(5)
Диагональные миноры определяются соотношениями
 (6)
(6)
Рассмотрим частные случаи
1. Для системы первого порядка (n = 1) характеристическое уравнение имеет вид:
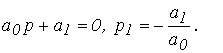 Условие устойчивости:
Условие устойчивости: ![]()
2. Для системы второго порядка (n=2) характеристическое уравнение имеет вид:
3.
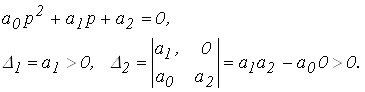
Условие
устойчивости: ![]()
4. Для системы третьего порядка (n = 3) характеристическое уравнение имеет вид:
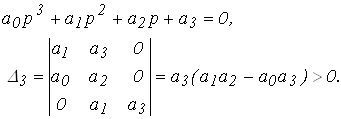
Условие
устойчивости:![]()
Для систем 1-го и 2-го порядка положительность
коэффициентов характеристического уравнения является необходимым и достаточным
условием устойчивости системы. Для системы 3-го порядка должно выполняться дополнительное
условие ![]()
Достоинство критерия:
1. Высокая точность, так как это алгебраический критерий.
2. Простота для систем невысокого порядка.
Недостатки критерия:
1. Необходимо иметь математическое описание системы.
2. Сложность применения для систем высокого порядка.
Рассмотрим примеры определения устойчивости по критерию Гурвица.
Пример 1. Определить
устойчивость системы, если ее характеристическое уравнение имеет вид:![]()
Условие
устойчивости ![]() не выполняется,
следовательно, система не устойчива.
не выполняется,
следовательно, система не устойчива.
Пример 2. Определить устойчивость если передаточная функция разомкнутой системы имеет вид
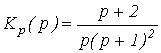 .
.
Решение:
1. Определяем передаточную функцию замкнутой системы
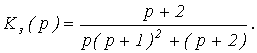
2. Запишем характеристическое уравнение и условие устойчивости
![]() .
.
Условие устойчивости выполняется, следовательно, система устойчива.
Пример 3. Для заданной системы (рис. 1) определить условие устойчивости и критический коэффициент усиления, т.е. коэффициент усиления, при котором система находится на границе устойчивости.
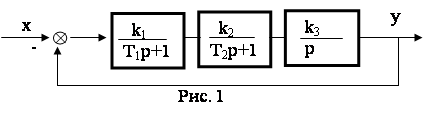
Решение:
3. Определяем передаточную функцию разомкнутой системы
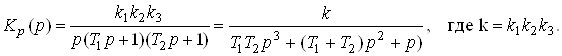
4. Определяем передаточную функцию замкнутой системы

5. Запишем характеристическое уравнение и условие устойчивости

4. Определим критический коэффициент усиления

3. Критерий устойчивости Михайлова
Для оценки устойчивости систем управления кроме алгебраических критериев, используются частотные критерии Михайлова и Найквиста.
Доказательство частотных критериев базируется на следствии из принципа аргумента.
Допустим, задан полином
 (7)
(7)
 |
|||
|
|||
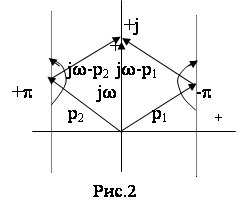
Если система n – го порядка содержит m неустойчивых полюсов, то угол поворота вектора D (jw) равен:
![]() (8)
(8)
Формулировка критерия Михайлова:
Замкнутая система автоматического управления устойчива, если характеристическая кривая (годограф Михайлова), начинаясь на положительной вещественной оси в точке an, при изменении частоты 0£ w £ ¥ последовательно проходит число квадрантов равное степени характеристического полинома.
При этом
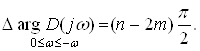 (9)
(9)
Пример 4. Допустим, задан характеристический полином системы

Годограф устойчивой системы имеет вид (рис. 3a).
Пример 5. Допустим, задан характеристический полином системы
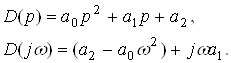
Годограф устойчивой системы имеет вид (рис. 3б).
Пример 6. Допустим, задан характеристический полином системы
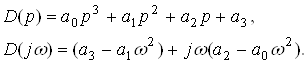
Годограф устойчивой системы имеет вид (рис. 3в).
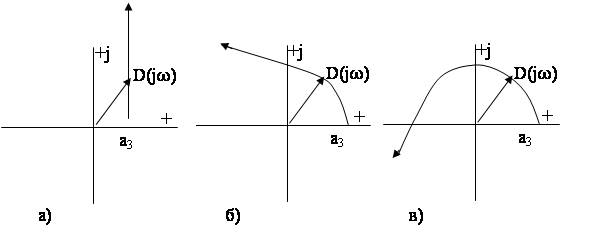
Рис. 3
Пример. Для заданной системы (рис. 4) определить условие устойчивости, частоту собственных колебаний системы и критический коэффициент усиления, т.е. коэффициент усиления, при котором система находится на границе устойчивости.
Определить устойчивость при T1 = T2 = 1 c и kv = 1 c-1.
Решение:
1. Определяем передаточную функцию разомкнутой системы
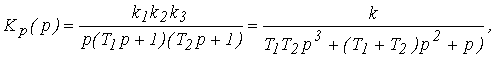
где![]()
2. Определяем передаточную функцию замкнутой системы

3. Запишем характеристическое уравнение
![]()
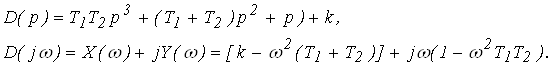
4. Определим частоту собственных колебаний системы и критический коэффициент усиления из условия границы устойчивости

Откуда частота собственных колебаний системы равна:
Критический коэффициент усиления равен:
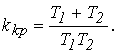
5. Определим устойчивость при T1 = T2 = 1 c и kv = 1 c-1.
![]()
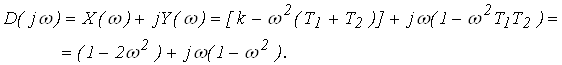
5. Строим
характеристическую кривую![]() (рис. 5)
по данным, приведенным в таблице 1.
(рис. 5)
по данным, приведенным в таблице 1.
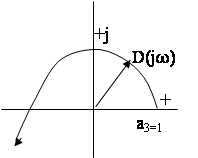
Таблица 1
| w | 0 |
|
1 | ¥ | ||
| X(w) | 1 | 0 | -1 | -¥ | ||
|
|
0 |
|
0 | -¥ |
В соответствии с критерием Михайлова, рассматриваемая система является устойчивой.
4. Частотный критерий устойчивости Найквиста
Частотный критерий устойчивости Найквиста позволяет по виду частотной характеристики разомкнутой системы судить об устойчивости замкнутой системы, т.е. он применим для замкнутых систем.
Рассмотрим функцию, которая связывает характеристики разомкнутых и замкнутых систем
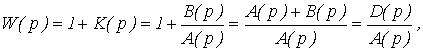 (6)
(6)
где D(p) – характеристический полином замкнутой системы;
A(p) – характеристический полином разомкнутой системы.
При этом степени полиномов A(p) и D(p) одинаковы исходя из условия физической реализуемости системы.
В соответствии со следствием из принципа аргумента
![]() (7)
(7)
Рассмотрим разные случаи.
Система, устойчивая в разомкнутом состоянии.
Так как разомкнутая система устойчива, то она не содержит корней в правой полуплоскости (т.е. m = 0), для того чтобы и замкнутая система была устойчива, должно выполняться условие:
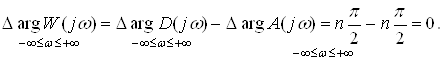 (8)
(8)
Графически это обозначает, что годограф вектора W (jw) не охватывает начала координат, а вектора K (jw) – точку с координатами (-1, j0), как показано на рис. 6. Точка с координатами (-1, j0) называется критической.

Рис. 6.
Система, неустойчивая в разомкнутом состоянии.
Так как разомкнутая система неустойчива, то она содержит m корней в правой полуплоскости, для того, чтобы замкнутая система была устойчивой, должно выполняться условие
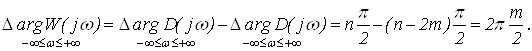 (9)
(9)
Графически это обозначает, что годограф вектора K (jw) охватывает точку с координатами (-1, j0) m/2 – раз.
Формулировка критерия Найквиста: Замкнутая система автоматического управления устойчива, если амплитудно-фазовая частотная характеристика разомкнутой, неустойчивой системы, имеющей m корней в правой полуплоскости, охватывает точку с координатами (–1, j0) m/2-раз.
Иногда по графику трудно определить охватывает ли АФХ критическую точку. В этом случае можно использовать правило переходов. Переходами называются точки пересечения АФХ отрезка оси (-¥.. – 1). Знак перехода определяется по следующему правилу: если фаза убывает – переход отрицательный.
Формулировка критерия Найквиста: Замкнутая система автома-тического управления устойчива, если разность положительных и отрицательных переходов равна m/2, где m – количество корней в правой полуплоскости разомкнутой неустойчивой системы, т.е.
|
(10)
Пример 8. Для заданной системы (рис. 7) определить условие устойчивости и критический коэффициент усиления.
Определить устойчивость при T1 = T2 = 1 c и kv = 1 c-1.
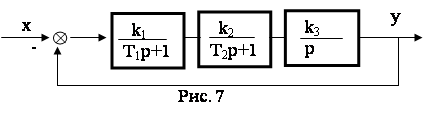
Решение:
1. Определяем передаточную функцию разомкнутой системы
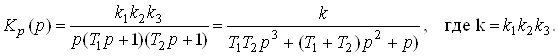
2. Строим АФХ разомкнутой системы

При T1 = T2 = 1 c и kv = 1 c-1 АФХ разомкнутой системы имеет вид
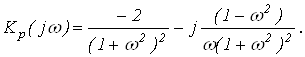
Расчетные данные приведены в таблице 2, а график АФХ на рис. 8.
Таблица 2
| w | 0 | 1 | ¥ | ||||
| P(w) | -2 | -1/2 | 0 | ||||
| Q(w) | -¥ |
|
0 |
|
Как видно из рисунка (8) и таблицы 2, АФХ разомкнутой системы не охватывает критическую точку, следовательно, замкнутая система, при заданной структуре и параметрах, устойчива.
Определим критический коэффициент усиления из условия:

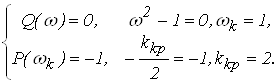
5. Определение областей устойчивости
Устойчивость систем зависит от структуры и параметров системы. При расчете систем автоматического управления возникает задача опреде-ления диапазона изменения варьируемых параметров системы, при кото-рых она устойчива.
Область устойчивости – это совокупность значений параметров системы, при которых она устойчива.
Коэффициенты характеристического уравнения являются функциями от параметров системы, и они определяют расположение корней в комплексной плоскости, при изменении параметров корни перемещаются в комплексной плоскости и система может стать не устойчивой.
Для определения областей устойчивости можно использовать различные методы, наиболее часто используют метод D – разбиения. D-разбиение может быть выполнено по одному и более параметрам.
Рассмотрим алгоритм определения областей устойчивости с помощью метода D – разбиения по одному параметру на конкретных примерах.
Пример 9. Определить область возможных значений параметра «к», при которых заданная система (рис. 9) устойчива
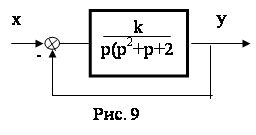
Порядок определения областей устойчивости
1. Определяем передаточную функцию замкнутой системы

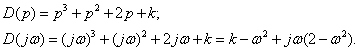
2. Определяем характеристический полином
3. Разрешим уравнение относительно параметра – к
![]()
4. Строим кривую D – разбиения (см. таблицу 3 и рис. 10)
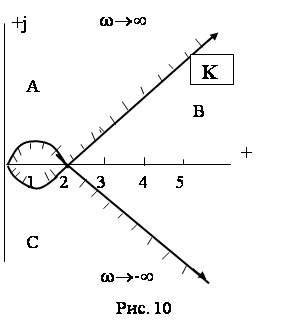
Таблица 3
| w | 0 | 1 | Ö2 | 2 | ¥ |
| X(w) | 0 | 1 | 2 | 4 | ¥ |
| Y(w) | 0 | -1 | 0 | 4 | ¥ |
|
|
Так как параметр является вещественной положительной величиной, то областью устойчивости являются значения параметра – к, расположенные на вещественной положительной оси, т.е.] 0, 2 [, что может быть провере-но по критерию Гурвица.
Литература
1. Бронштейн И.Н., Семендяев К.Н. Справочник по математике для инженеров и учащихся вузов. – М.: Наука, 1986.
2. Брюханов В.Н. и др. Теория автоматического управления. – М: Высшая школа, 2000.
3. Егупов Н.Д., Пупков К.А., Баркин А.И. Синтез регуляторов систем автоматического управления. МГТУ им. Н.Э. Баумана, 2004.
4. Ким Д.П., Дмитриева Н.Д. Сборник задач по теории автоматического управления. Линейные системы. ФИЗМАТЛИТ, 2007. – 168 с.
5. Лукас В.А. Теория автоматического управления. – М.: Недра, 1990. – 416 с.
6. Сборник задач по теории автоматического регулирования и управления/ Под редакцией В.А. Бесекерского. – M.: Наука, 1978.
7. Справочник по теории автоматического управления. /Под ред. А.А. Красовского – М.: Наука, 198 – 712 с.