
Рефераты по авиации и космонавтике
Рефераты по административному праву
Рефераты по безопасности жизнедеятельности
Рефераты по арбитражному процессу
Рефераты по архитектуре
Рефераты по астрономии
Рефераты по банковскому делу
Рефераты по сексологии
Рефераты по информатике программированию
Рефераты по биологии
Рефераты по экономике
Рефераты по москвоведению
Рефераты по экологии
Краткое содержание произведений
Рефераты по физкультуре и спорту
Топики по английскому языку
Рефераты по математике
Рефераты по музыке
Остальные рефераты
Рефераты по биржевому делу
Рефераты по ботанике и сельскому хозяйству
Рефераты по бухгалтерскому учету и аудиту
Рефераты по валютным отношениям
Рефераты по ветеринарии
Рефераты для военной кафедры
Рефераты по географии
Рефераты по геодезии
Рефераты по геологии
Рефераты по геополитике
Рефераты по государству и праву
Рефераты по гражданскому праву и процессу
Рефераты по кредитованию
Рефераты по естествознанию
Рефераты по истории техники
Рефераты по журналистике
Рефераты по зоологии
Рефераты по инвестициям
Рефераты по информатике
Исторические личности
Рефераты по кибернетике
Рефераты по коммуникации и связи
Рефераты по косметологии
Рефераты по криминалистике
Рефераты по криминологии
Рефераты по науке и технике
Рефераты по кулинарии
Рефераты по культурологии
Контрольная работа: Прогнозирование на основе регрессионных моделей
Контрольная работа: Прогнозирование на основе регрессионных моделей
По имеющимся исходным данным выявить и оценить на основе регрессионных моделей производственные связи. Провести расчет прогнозных значений показателей, когда уровень факторных показателей на 30% превышают средние величины исходных данных.
Исходные данные представлены в таблице:
|
№ |
Удой молока на среднегодовую корову, кг |
Расход кормов на 1 корову, корм. ед. |
Удельный вес чистопородных коров в стаде, % |
Себестоимость молока за 1 кг, руб. |
| 1 | 3280 | 48,20 | 61 | 0,313 |
| 2 | 2920 | 43,10 | 54 | 0,413 |
| 3 | 5140 | 60,70 | 70 | 0,268 |
| 4 | 4630 | 60,10 | 67 | 0,310 |
| 5 | 4950 | 59,40 | 71 | 0,309 |
| 6 | 5000 | 52,50 | 74 | 0,288 |
| 7 | 2790 | 44,00 | 45 | 0,357 |
| 8 | 4340 | 54,20 | 68 | 0,247 |
| 9 | 4160 | 53,20 | 65 | 0,305 |
| 10 | 2660 | 46,40 | 51 | 0,376 |
| 11 | 2960 | 47,10 | 52 | 0,351 |
| 12 | 3230 | 46,10 | 57 | 0,356 |
| 13 | 3480 | 53,90 | 58 | 0,312 |
| 14 | 3230 | 53,40 | 52 | 0,415 |
| 15 | 2370 | 39,40 | 44 | 0,411 |
| 16 | 2610 | 40,20 | 50 | 0,380 |
| 17 | 3000 | 45,50 | 52 | 0,326 |
| 18 | 2960 | 41,40 | 49 | 0,341 |
| 19 | 3100 | 47,80 | 53 | 0,398 |
| 20 | 2720 | 46,30 | 57 | 0,405 |
Необходимо определить
тесноту связи между данными признаками. Для этого вначале воспользуемся коэффициентом
корреляции рангов Спирмэна. Этот показатель основан на корреляции не самих
значений коррелируемых признаков, а их рангов. Для его расчета присвоим ранги
значениям соответствующих признаков, затем найдем их разность d. Эти вычисления
отразим в нижеследующих таблицах. Далее вычислим непосредственно сам
коэффициент, который равен: ![]() , (
n – число наблюдаемых пар значений признаков.)
, (
n – число наблюдаемых пар значений признаков.)
Расчетные таблицы для определения коэффициента корреляции рангов Спирмэна
| Удой молока на среднегодовую корову, кг | Себестоимость молока за 1 кг, руб. | Ранги | Разность рангов d = Nx - Ny |
d2 |
||
| x | y |
Nx |
Ny |
|||
| 3280 | 0,313 | 8 | 13 | -5 | 25 | |
| 2920 | 0,413 | 15 | 2 | 13 | 169 | |
| 5140 | 0,268 | 1 | 19 | -18 | 324 | |
| 4630 | 0,31 | 4 | 15 | -11 | 121 | |
| 4950 | 0,309 | 3 | 16 | -13 | 169 | |
| 5000 | 0,288 | 2 | 18 | -16 | 256 | |
| 2790 | 0,357 | 16 | 8 | 8 | 64 | |
| 4340 | 0,247 | 5 | 20 | -15 | 225 | |
| 4160 | 0,305 | 6 | 17 | -11 | 121 | |
| 2660 | 0,376 | 18 | 7 | 11 | 121 | |
| 2960 | 0,351 | 13,5 | 10 | 3,5 | 12,25 | |
| 3230 | 0,356 | 9,5 | 9 | 0,5 | 0,25 | |
| 3480 | 0,312 | 7 | 14 | -7 | 49 | |
| 3230 | 0,415 | 9,5 | 1 | 8,5 | 72,25 | |
| 2370 | 0,411 | 20 | 3 | 17 | 289 | |
| 2610 | 0,38 | 19 | 6 | 13 | 169 | |
| 3000 | 0,326 | 12 | 12 | 0 | 0 | |
| 2960 | 0,341 | 13,5 | 11 | 2,5 | 6,25 | |
| 3100 | 0,398 | 11 | 5 | 6 | 36 | |
| 2720 | 0,405 | 17 | 4 | 13 | 169 | |
| n = 20 |
∑ d 2 = |
2398 | ||||
| ρ = | -0,803 | |||||
Из выше приведенного можно сказать о сильной обратной связи между удоем молока и себестоимостью, т.е. при увеличении удоя себестоимость молока снижается.
| Расход кормов на 1 корову, корм.ед. | Себестоимость молока за 1 кг, руб. | Ранги | Разность рангов d = Nx - Ny |
d2 |
||
| x | y |
Nx |
Ny |
|||
| 48,2 | 0,313 | 9 | 13 | -4 | 16 | |
| 43,1 | 0,413 | 17 | 2 | 15 | 225 | |
| 60,7 | 0,268 | 1 | 19 | -18 | 324 | |
| 60,1 | 0,31 | 2 | 15 | -13 | 169 | |
| 59,4 | 0,309 | 3 | 16 | -13 | 169 | |
| 52,5 | 0,288 | 8 | 18 | -10 | 100 | |
| 44 | 0,357 | 16 | 8 | 8 | 64 | |
| 54,2 | 0,247 | 4 | 20 | -16 | 256 | |
| 53,2 | 0,305 | 7 | 17 | -10 | 100 | |
| 46,4 | 0,376 | 12 | 7 | 5 | 25 | |
| 47,1 | 0,351 | 11 | 10 | 1 | 1 | |
| 46,1 | 0,356 | 14 | 9 | 5 | 25 | |
| 53,9 | 0,312 | 5 | 14 | -9 | 81 | |
| 53,4 | 0,415 | 6 | 1 | 5 | 25 | |
| 39,4 | 0,411 | 20 | 3 | 17 | 289 | |
| 40,2 | 0,38 | 19 | 6 | 13 | 169 | |
| 45,5 | 0,326 | 15 | 12 | 3 | 9 | |
| 41,4 | 0,341 | 18 | 11 | 7 | 49 | |
| 47,8 | 0,398 | 10 | 5 | 5 | 25 | |
| 46,3 | 0,405 | 13 | 4 | 9 | 81 | |
| n = 20 |
∑ d 2 = |
2202 | ||||
| ρ = | -0,656 | |||||
Так как значение коэффициента отрицательно, следовательно, имеем обратную связь между расходом кормов на 1 корову и себестоимостью молока.
Удельный вес чистопородных коров в стаде, % |
Себестоимость молока за 1 кг, руб. | Ранги | Разность рангов d = Nx - Ny |
d2 |
||
| x | y |
Nx |
Ny |
|||
| 61 | 0,313 | 7 | 13 | -6 | 36 | |
| 54 | 0,413 | 11 | 2 | 9 | 81 | |
| 70 | 0,268 | 3 | 19 | -16 | 256 | |
| 67 | 0,31 | 5 | 15 | -10 | 100 | |
| 71 | 0,309 | 2 | 16 | -14 | 196 | |
| 74 | 0,288 | 1 | 18 | -17 | 289 | |
| 45 | 0,357 | 19 | 8 | 11 | 121 | |
| 68 | 0,247 | 4 | 20 | -16 | 256 | |
| 65 | 0,305 | 6 | 17 | -11 | 121 | |
| 51 | 0,376 | 16 | 7 | 9 | 81 | |
| 52 | 0,351 | 13 | 10 | 3 | 9 | |
| 57 | 0,356 | 9 | 9 | 0 | 0 | |
| 58 | 0,312 | 8 | 14 | -6 | 36 | |
| 52 | 0,415 | 13 | 1 | 12 | 144 | |
| 44 | 0,411 | 20 | 3 | 17 | 289 | |
| 50 | 0,38 | 17 | 6 | 11 | 121 | |
| 52 | 0,326 | 13 | 12 | 1 | 1 | |
| 49 | 0,341 | 18 | 11 | 7 | 49 | |
| 53 | 0,398 | 12 | 5 | 7 | 49 | |
| 57 | 0,405 | 9 | 4 | 5 | 25 | |
| n = 20 |
∑ d 2 = |
2260 | ||||
| ρ = | -0,699 | |||||
Имеется обратная зависимости между удельным весом чистопородных коров в стаде и себестоимостью молока.
| Удой молока на среднегодовую корову, кг | Расход кормов на 1 корову, корм.ед. | Ранги | Разность рангов d = Nx - Ny |
d2 |
||
| x | y |
Nx |
Ny |
|||
| 3280 | 48,2 | 8 | 9 | -1 | 1 | |
| 2920 | 43,1 | 15 | 17 | -2 | 4 | |
| 5140 | 60,7 | 1 | 1 | 0 | 0 | |
| 4630 | 60,1 | 4 | 2 | 2 | 4 | |
| 4950 | 59,4 | 3 | 3 | 0 | 0 | |
| 5000 | 52,5 | 2 | 8 | -6 | 36 | |
| 2790 | 44 | 16 | 16 | 0 | 0 | |
| 4340 | 54,2 | 5 | 4 | 1 | 1 | |
| 4160 | 53,2 | 6 | 7 | -1 | 1 | |
| 2660 | 46,4 | 18 | 12 | 6 | 36 | |
| 2960 | 47,1 | 13,5 | 11 | 2,5 | 6,25 | |
| 3230 | 46,1 | 9,5 | 14 | -4,5 | 20,25 | |
| 3480 | 53,9 | 7 | 5 | 2 | 4 | |
| 3230 | 53,4 | 9,5 | 6 | 3,5 | 12,25 | |
| 2370 | 39,4 | 20 | 20 | 0 | 0 | |
| 2610 | 40,2 | 19 | 19 | 0 | 0 | |
| 3000 | 45,5 | 12 | 15 | -3 | 9 | |
| 2960 | 41,4 | 13,5 | 18 | -4,5 | 20,25 | |
| 3100 | 47,8 | 11 | 10 | 1 | 1 | |
| 2720 | 46,3 | 17 | 13 | 4 | 16 | |
| n = 20 |
∑ d 2 = |
172 | ||||
| ρ = | 0,871 | |||||
Полученное значение коэффициента корреляции рангов Спирмэна свидетельствует о сильной прямой связи между удоем молока и расходом кормов на 1 корову, т.е. при увеличении расхода кормов в пересчете на 1 корову увеличивается и удой молока на среднегодовую корову.
| Удой молока на среднегодовую корову, кг | Удельный вес чистопородных коров в стаде, % | Ранги | Разность рангов d = Nx - Ny |
d2 |
||
| x | y |
Nx |
Ny |
|||
| 3280 | 61 | 8 | 7 | 1 | 1 | |
| 2920 | 54 | 15 | 11 | 4 | 16 | |
| 5140 | 70 | 1 | 3 | -2 | 4 | |
| 4630 | 67 | 4 | 5 | -1 | 1 | |
| 4950 | 71 | 3 | 2 | 1 | 1 | |
| 5000 | 74 | 2 | 1 | 1 | 1 | |
| 2790 | 45 | 16 | 19 | -3 | 9 | |
| 4340 | 68 | 5 | 4 | 1 | 1 | |
| 4160 | 65 | 6 | 6 | 0 | 0 | |
| 2660 | 51 | 18 | 16 | 2 | 4 | |
| 2960 | 52 | 13,5 | 13 | 0,5 | 0,25 | |
| 3230 | 57 | 9,5 | 9 | 0,5 | 0,25 | |
| 3480 | 58 | 7 | 8 | -1 | 1 | |
| 3230 | 52 | 9,5 | 13 | -3,5 | 12,25 | |
| 2370 | 44 | 20 | 20 | 0 | 0 | |
| 2610 | 50 | 19 | 17 | 2 | 4 | |
| 3000 | 52 | 12 | 13 | -1 | 1 | |
| 2960 | 49 | 13,5 | 18 | -4,5 | 20,25 | |
| 3100 | 53 | 11 | 12 | -1 | 1 | |
| 2720 | 57 | 17 | 9 | 8 | 64 | |
| n = 20 |
∑ d 2 = |
142 | ||||
| ρ = | 0,893 | |||||
Значение положительно, поэтому имеемхарактеризует сильную прямую связь между удоем молока и удельным весом чистопородных коров в стаде и показывает, что вариация результативного признака на 89,3 % обусловлена вариацией факторного признака (согласно коэффициенту Спирмэна).
| Расход кормов на 1 корову, корм.ед. | Удельный вес чистопородных коров в стаде, % | Ранги | Разность рангов d = Nx - Ny |
d2 |
||
| x | y |
Nx |
Ny |
|||
| 48,2 | 61 | 9 | 7 | 2 | 4 | |
| 43,1 | 54 | 17 | 11 | 6 | 36 | |
| 60,7 | 70 | 1 | 3 | -2 | 4 | |
| 60,1 | 67 | 2 | 5 | -3 | 9 | |
| 59,4 | 71 | 3 | 2 | 1 | 1 | |
| 52,5 | 74 | 8 | 1 | 7 | 49 | |
| 44 | 45 | 16 | 19 | -3 | 9 | |
| 54,2 | 68 | 4 | 4 | 0 | 0 | |
| 53,2 | 65 | 7 | 6 | 1 | 1 | |
| 46,4 | 51 | 12 | 16 | -4 | 16 | |
| 47,1 | 52 | 11 | 13 | -2 | 4 | |
| 46,1 | 57 | 14 | 9 | 5 | 25 | |
| 53,9 | 58 | 5 | 8 | -3 | 9 | |
| 53,4 | 52 | 6 | 13 | -7 | 49 | |
| 39,4 | 44 | 20 | 20 | 0 | 0 | |
| 40,2 | 50 | 19 | 17 | 2 | 4 | |
| 45,5 | 52 | 15 | 13 | 2 | 4 | |
| 41,4 | 49 | 18 | 18 | 0 | 0 | |
| 47,8 | 53 | 10 | 12 | -2 | 4 | |
| 46,3 | 57 | 13 | 9 | 4 | 16 | |
| n = 20 |
∑ d 2 = |
244 | ||||
| ρ = | 0,817 | |||||
О сильной прямой зависимости между расходом кормов в пересчете на 1 корову и удельным весом чистопородных коров в стаде говорит значение коэффициента. Чем выше удельный вес, тем выше расход кормов.
Но следует иметь в виду, что, поскольку коэффициент Спирмэна учитывает разность только рангов, а не самих значений признаков, он менее точен по сравнению с линейным коэффициентом корреляции. Воспользуемся последним.
Воспользуемся программным пакетом Stata 7.
Корреляционная матрица имеет вид:
. corr ud korm ves sst
(obs=20)
| ud korm ves sst
-------------+------------------------------------
ud | 1.0000
korm | 0.8851 1.0000
ves | 0.9401 0.8290 1.0000
sst | -0.7875 -0.6497 -0.7587 1.0000
· ud – удой молока на среднегодовую корову,
· korm – расход кормов на 1 корову,
· ves – удельный вес чистопородных коров в стаде,
· sst – себестоимость молока за 1 кг.
Можно сделать вывод, что присутствует обратная связь между себестоимостью и удоем молока (r = - 0,79), себестоимостью и удельным весом (r = - 0,76),себестоимостью и расходом кормов (r = - 0,65).Имеется сильная прямая связи между удоем молока и расходом кормов (r = 0,89), удоем молока и удельным весом (r = 0,94), расходом кормов и удельным весом (r = 0,83). Если сравнивать значения, полученные линейным коэффициентом корреляции и ранговым коэффициентом Спирмэна, то расхождения не превысят 8 %. В большинстве же своем погрешность составляет около 1 %.
Теперь проверим коэффициенты корреляции на значимость:
. pwcorr ud korm ves sst
| ud korm ves sst
-------------+------------------------------------
ud | 1.0000
korm | 0.8851 1.0000
ves | 0.9401 0.8290 1.0000
sst | -0.7875 -0.6497 -0.7587 1.0000
Все коэффициенты значимы.
Построим модель.
Так как значения удоя молока и значения других показателей отличаются на порядок, то будем использовать вместо переменной «удой молока» переменную натурального логарифма удоя молока.
Рассмотрим в качестве результативного фактора себестоимость молока за 1 кг, поскольку важен расчет именно себестоимости и определение от каких факторов и насколько она зависит. Удой молока, расход кормов на 1 корову и удельный вес чистопородных коров в стаде могут повлиять на значение себестоимости.
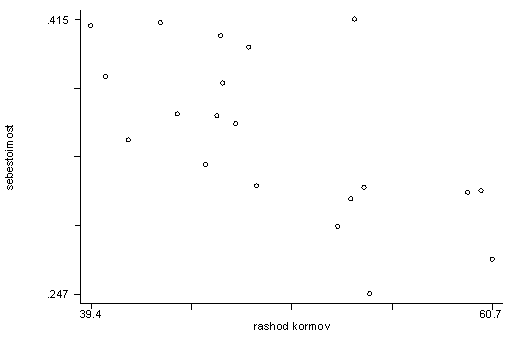
Приведем графики зависимости себестоимости от каждого из факторов:
От логарифма удоя молока

От расхода кормов на 1 корову
От удельного веса чистопородных коров в стаде
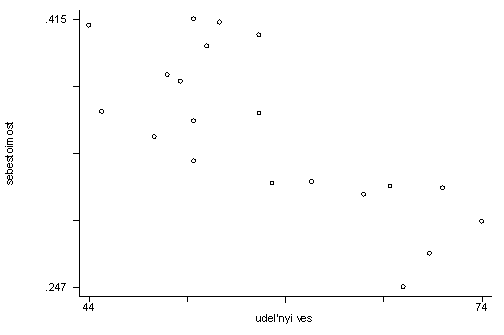
Графики демонстрируют нам обратную зависимость между результативным фактором – себестоимостью и объясняющим фактором, что подтверждается значениями коэффициентов корреляции.
Вначале рассмотрим линейную модель по всем факторам:
. reg sst lnud korm ves
Source | SS df MS Number of obs = 20
-------------+------------------------------ F( 3, 16) = 10.37
Model | .031800232 3 .010600077 Prob > F = 0.0005
Residual | .016350718 16 .00102192 R-squared = 0.6604
-------------+------------------------------ Adj R-squared = 0.5968
Total | .04815095 19 .002534261 Root MSE = .03197
------------------------------------------------------------------------------
sst | Coef. Std. Err. t P>|t| [95% Conf. Interval]
-------------+----------------------------------------------------------------
lnud | -.2305787 .1162704 -1.98 0.065 -.4770609 .0159036
korm | .0026417 .0025775 1.02 0.321 -.0028223 .0081057
ves | -.0000138 .0024772 -0.01 0.996 -.0052651 .0052376
_cons | 2.088534 .7538614 2.77 0.014 .4904194 3.686649
------------------------------------------------------------------------------
Хотя у этой модели и достаточно хороший коэффициент детерминации и согласно F-критерию Фишера оно значимо, параметры при переменных lnud, korm, ves не значимы по t-критерию Стьюдента с P-значениями 0.065, 0.321 и 0.996. Значит, эта модель не подходит.
Построим модель вида: ![]()
. reg sst lnud1 korm1 ves1
Source | SS df MS Number of obs = 20
-------------+------------------------------ F( 3, 16) = 10.32
Model | .031744654 3 .010581551 Prob > F = 0.0005
Residual | .016406296 16 .001025393 R-squared = 0.6593
-------------+------------------------------ Adj R-squared = 0.5954
Total | .04815095 19 .002534261 Root MSE = .03202
------------------------------------------------------------------------------
sst | Coef. Std. Err. t P>|t| [95% Conf. Interval]
-------------+----------------------------------------------------------------
lnud1 | 14.46292 6.110319 2.37 0.031 1.509625 27.41622
korm1 | -5.633853 5.967609 -0.94 0.359 -18.28462 7.016912
ves1 | .6831225 6.892859 0.10 0.922 -13.92909 15.29533
_cons | -1.33304 .6029802 -2.21 0.042 -2.611301 -.0547791
------------------------------------------------------------------------------
Видим что коэффициент детерминации хорош - 0,659 и по F-критерию Фишера уравнение значимо. Но параметры при переменных korm1, ves1 не значимы по t-критерию Стьюдента с P-значениями 0.359 и 0.922. Значит, эта модель не подходит.
Будем рассматривать
различные комбинации переменных при включении в модель. Построим модель вида: ![]()
. reg sst lnud korm1 ves1
Source | SS df MS Number of obs = 20
-------------+------------------------------ F( 3, 16) = 10.09
Model | .031497211 3 .01049907 Prob > F = 0.0006
Residual | .016653739 16 .001040859 R-squared = 0.6541
-------------+------------------------------ Adj R-squared = 0.5893
Total | .04815095 19 .002534261 Root MSE = .03226
------------------------------------------------------------------------------
sst | Coef. Std. Err. t P>|t| [95% Conf. Interval]
-------------+----------------------------------------------------------------
lnud | -.2065493 .0898758 -2.30 0.035 -.3970775 -.0160212
korm1 | -5.156249 5.939941 -0.87 0.398 -17.74836 7.435864
ves1 | 1.094516 6.895036 0.16 0.876 -13.52231 15.71134
_cons | 2.109487 .8816345 2.39 0.029 .2405058 3.978469
------------------------------------------------------------------------------
Так же как и в предыдущих моделях, значение R-квадрата хорошее, уравнение значимо по F-критерию Фишера, но одновременно с этим параметры при переменных korm1, ves1 с P-значениями 0.398 и 0.876 соответственно не значимы по t-критерию Стьюдента. Также отбросим эту модель.
Построим модель вида: ![]()
. reg sst lnud1 korm ves1
Source | SS df MS Number of obs = 20
-------------+------------------------------ F( 3, 16) = 10.60
Model | .032029999 3 .010676666 Prob > F = 0.0004
Residual | .016120951 16 .001007559 R-squared = 0.6652
-------------+------------------------------ Adj R-squared = 0.6024
Total | .04815095 19 .002534261 Root MSE = .03174
------------------------------------------------------------------------------
sst | Coef. Std. Err. t P>|t| [95% Conf. Interval]
-------------+----------------------------------------------------------------
lnud1 | 15.74117 6.497854 2.42 0.028 1.966333 29.516
korm | .0027978 .0025644 1.09 0.291 -.0026386 .0082341
ves1 | .0207899 6.780318 0.00 0.998 -14.35284 14.39442
_cons | -1.732706 .8136604 -2.13 0.049 -3.457589 -.0078235
------------------------------------------------------------------------------
R-квадрат хорош- 0,665, уравнение значимо согласно F-критерию Фишера. Но при этом параметры при переменных korm, ves1 с P-значениями 0.291 и 0.998 соответственно не значимы по t-критерию Стьюдента. Также отбросим эту модель.
Рассмотрим модель: ![]()
. reg sst lnud1 korm1 ves
Source | SS df MS Number of obs = 20
-------------+------------------------------ F( 3, 16) = 10.31
Model | .031738225 3 .010579408 Prob > F = 0.0005
Residual | .016412725 16 .001025795 R-squared = 0.6591
-------------+------------------------------ Adj R-squared = 0.5952
Total | .04815095 19 .002534261 Root MSE = .03203
------------------------------------------------------------------------------
sst | Coef. Std. Err. t P>|t| [95% Conf. Interval]
-------------+----------------------------------------------------------------
lnud1 | 14.53007 7.378598 1.97 0.066 -1.111856 30.172
korm1 | -5.544031 5.927707 -0.94 0.364 -18.11021 7.022147
ves | -.0001462 .002454 -0.06 0.953 -.0053485 .005056
_cons | -1.322613 .969369 -1.36 0.191 -3.377583 .7323579
------------------------------------------------------------------------------
Как и в предыдущих моделях, несмотря на значимость уравнения и хорошее значение коэффициента детерминации, эту регрессионную модель мы также отбросим, так как в ней незначимы параметры при переменных lnud1, korm1, ves согласно t-критерию Стьюдента.
Рассмотрим модель:
![]()
. reg sst lnud lnud2 korm korm2 ves ves2
Source | SS df MS Number of obs = 20
-------------+------------------------------ F( 6, 13) = 4.52
Model | .032557159 6 .005426193 Prob > F = 0.0109
Residual | .015593791 13 .001199522 R-squared = 0.6761
-------------+------------------------------ Adj R-squared = 0.5267
Total | .04815095 19 .002534261 Root MSE = .03463
------------------------------------------------------------------------------
sst | Coef. Std. Err. t P>|t| [95% Conf. Interval]
-------------+----------------------------------------------------------------
lnud | -5.729043 9.44621 -0.61 0.555 -26.13634 14.67825
lnud2 | .341597 .5910669 0.58 0.573 -.9353253 1.618519
korm | .0132344 .0388671 0.34 0.739 -.0707327 .0972016
korm2 | -.0001134 .0004041 -0.28 0.783 -.0009865 .0007596
ves | .0150622 .0364293 0.41 0.686 -.0636385 .0937629
ves2 | -.0001446 .0003466 -0.42 0.683 -.0008934 .0006042
_cons | 23.57414 36.19652 0.65 0.526 -54.62369 101.772
------------------------------------------------------------------------------
Эта модель также не подходит, поскольку параметры при всех переменных не значимы согласно t-критерию Стьюдента.
Рассмотрим модель: ![]()
. reg sst lnud2 korm2 ves2
Source | SS df MS Number of obs = 20
-------------+------------------------------ F( 3, 16) = 10.39
Model | .031819188 3 .010606396 Prob > F = 0.0005
Residual | .016331762 16 .001020735 R-squared = 0.6608
-------------+------------------------------ Adj R-squared = 0.5972
Total | .04815095 19 .002534261 Root MSE = .03195
------------------------------------------------------------------------------
sst | Coef. Std. Err. t P>|t| [95% Conf. Interval]
-------------+----------------------------------------------------------------
lnud2 | -.0150021 .0079436 -1.89 0.077 -.0318418 .0018377
korm2 | .000028 .0000263 1.07 0.302 -.0000277 .0000838
ves2 | 2.49e-06 .0000227 0.11 0.914 -.0000457 .0000507
_cons | 1.258054 .4178871 3.01 0.008 .3721731 2.143935
------------------------------------------------------------------------------
И в этой модели параметры при переменных не значимы по t-критерию Стьюдента. Отбрасываем эту модель.
Воспользуемся процедурой
пошагового отбора регрессоров при построении множественной регрессии. При этом
из исходного набора объясняющих переменных будут включаться в число регрессоров
в первую очередь те переменные, которые имеют больший уровень значимости. Вначале
включим в набор переменных переменную ![]() , а затем переменную
, а затем переменную ![]() .
.
. sw reg sst lnud korm ves korm1 ves1 lnud2 korm2 ves2,pe(0.05)
begin with empty model
p = 0.0000 < 0.0500 adding lnud
Source | SS df MS Number of obs = 20
-------------+------------------------------ F( 1, 18) = 31.70
Model | .030711968 1 .030711968 Prob > F = 0.0000
Residual | .017438982 18 .000968832 R-squared = 0.6378
-------------+------------------------------ Adj R-squared = 0.6177
Total | .04815095 19 .002534261 Root MSE = .03113
------------------------------------------------------------------------------
sst | Coef. Std. Err. t P>|t| [95% Conf. Interval]
-------------+----------------------------------------------------------------
lnud | -.1672727 .0297095 -5.63 0.000 -.22969 -.1048553
_cons | 1.703191 .241499 7.05 0.000 1.19582 2.210561
------------------------------------------------------------------------------
В итоге получили модель ![]() . Это уравнение значимо
согласно F-критерию Фишера, и параметр при переменной lnud и константа значимы по t-критерию Стьюдента. 63,78 %
суммы квадратов отклонений переменной sst от среднего значения объясняется
переменными модели. А при увеличении удоя молока на 2,72 % себестоимость
снижается на 0,17 %.
. Это уравнение значимо
согласно F-критерию Фишера, и параметр при переменной lnud и константа значимы по t-критерию Стьюдента. 63,78 %
суммы квадратов отклонений переменной sst от среднего значения объясняется
переменными модели. А при увеличении удоя молока на 2,72 % себестоимость
снижается на 0,17 %.
. sw reg sst lnud1 korm ves korm1 ves1 lnud2 korm2 ves2,pe(0.05)
begin with empty model
p = 0.0000 < 0.0500 adding lnud1
Source | SS df MS Number of obs = 20
-------------+------------------------------ F( 1, 18) = 32.04
Model | .030830369 1 .030830369 Prob > F = 0.0000
Residual | .017320581 18 .000962254 R-squared = 0.6403
-------------+------------------------------ Adj R-squared = 0.6203
Total | .04815095 19 .002534261 Root MSE = .03102
------------------------------------------------------------------------------
sst | Coef. Std. Err. t P>|t| [95% Conf. Interval]
-------------+----------------------------------------------------------------
lnud1 | 11.2229 1.982717 5.66 0.000 7.057366 15.38843
_cons | -1.038311 .2443161 -4.25 0.000 -1.5516 -.5250216
------------------------------------------------------------------------------
Получили модель ![]() . Это уравнение значимо по
F-критерию Фишера, и параметр при переменной lnud1 и константа значимы по t-критерию Стьюдента. 64,03 % суммы квадратов
отклонений переменной sst от среднего значения объясняется переменными модели.
. Это уравнение значимо по
F-критерию Фишера, и параметр при переменной lnud1 и константа значимы по t-критерию Стьюдента. 64,03 % суммы квадратов
отклонений переменной sst от среднего значения объясняется переменными модели.
Сделаем выбор между этими двумя моделями. Представим критерии выбора модели в следующей таблице:
| Модель | Критерий | ||||
| R-квадрат | Скорректированный R-квадрат | Акейка | Шварца |
σост |
|
|
|
0.6378 | 0.6177 | -13,9896 | -6,89499 | 0,0302959 |
|
|
0.6403 | 0.6203 | -14,0032 | -6,90180 | 0,03019289 |
Из данной таблицы видно, что по всем критериям гиперболическая модель лучше линейной.
Проверим регрессию на автокорреляцию остатков:
. regdw sst lnud1,t(lnud1) force
Source | SS df MS Number of obs = 20
-------------+------------------------------ F( 1, 18) = 32.04
Model | .030830369 1 .030830369 Prob > F = 0.0000
Residual | .017320581 18 .000962254 R-squared = 0.6403
-------------+------------------------------ Adj R-squared = 0.6203
Total | .04815095 19 .002534261 Root MSE = .03102
------------------------------------------------------------------------------
sst | Coef. Std. Err. t P>|t| [95% Conf. Interval]
-------------+----------------------------------------------------------------
lnud1 | 11.2229 1.982717 5.66 0.000 7.057366 15.38843
_cons | -1.038311 .2443161 -4.25 0.000 -1.5516 -.5250216
------------------------------------------------------------------------------
Durbin-Watson Statistic = 2.460766
Проверка на
автокорреляцию дает удовлетворительное значение статистики Дарбина-Уотсона 2,46
(автокорреляция отсутствует), так как ![]() ,
где
,
где ![]() (табличное значение). Это означает, что ошибки независимы
между собой.
(табличное значение). Это означает, что ошибки независимы
между собой.
Построим график остатков регрессии от оцененной зависимой переменной:
. fit sst lnud1
Source | SS df MS Number of obs = 20
-------------+------------------------------ F( 1, 18) = 32.04
Model | .030830369 1 .030830369 Prob > F = 0.0000
Residual | .017320581 18 .000962254 R-squared = 0.6403
-------------+------------------------------ Adj R-squared = 0.6203
Total | .04815095 19 .002534261 Root MSE = .03102
------------------------------------------------------------------------------
sst | Coef. Std. Err. t P>|t| [95% Conf. Interval]
-------------+----------------------------------------------------------------
lnud1 | 11.2229 1.982717 5.66 0.000 7.057366 15.38843
_cons | -1.038311 .2443161 -4.25 0.000 -1.5516 -.5250216
------------------------------------------------------------------------------
. rvfplot, c(m)
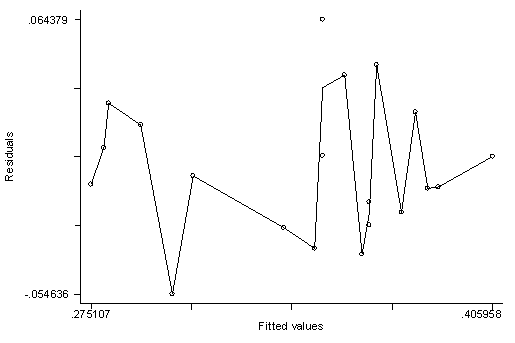
Можно предположить наличие гетероскедастичноти, поскольку разброс значений остатков увеличивается с ростом значений себестоимости молока. Проверим этот факт с помощью теста Бреуша-Пагана:
. hettest
Cook-Weisberg test for heteroskedasticity using fitted values of sst
Ho: Constant variance
chi2(1) = 0.01
Prob > chi2 = 0.9328
Тест Бреуша-Пагана подтверждает наличие гетероскедастичности, потому что гипотеза о постоянстве дисперсий отклоняется.
Скорректируем стандартные ошибки по Навье-Весту, учитывая гетероскедастичность:
. newey sst lnud1, lag(0) force
Regression with Newey-West standard errors Number of obs = 20
maximum lag : 0 F( 1, 18) = 60.26
Prob > F = 0.0000
------------------------------------------------------------------------------
| Newey-West
sst | Coef. Std. Err. t P>|t| [95% Conf. Interval]
-------------+----------------------------------------------------------------
lnud1 | 11.2229 1.445712 7.76 0.000 8.18557 14.26023
_cons | -1.038311 .1784612 -5.82 0.000 -1.413244 -.6633776
------------------------------------------------------------------------------
Изменились доверительные интервалы для параметров переменных модели.
Итак, имеем модель: ![]() ,
,
(sst-себестоимость молока за 1 кг, руб) ;
lnud-логарифм удоя молока на среднегодовую корову, кг.
Себестоимость не зависит
ни от расхода кормов на 1 корову, ни от удельного веса чистопородных коров в
стаде. Выявлена обратная пропорциональность между себестоимостью молока и
логарифмом удоя молока, а следовательно, и просто удоем молока. Стандартная
ошибка переменной ![]() составляет 1.4457, а константы – 0.1785.
Доверительный интервал для переменной
составляет 1.4457, а константы – 0.1785.
Доверительный интервал для переменной ![]() – [ 8.1856 ; 14.2602 ], для константы – [ -1.4132 ; -0.6634 ].
– [ 8.1856 ; 14.2602 ], для константы – [ -1.4132 ; -0.6634 ].
Рассчитаем прогнозные значения показателей, когда уровень факторных показателей на 30 % превышает средние величины исходных данных. Средний показатель удоя молока на среднегодовую корову равен 3476.5 кг. Превышение этого значения на 30 % составляет 4519.45 кг. Прологарифмируя, получим: lnud = 8.416. Тогда, согласно модели, себестоимость при таком значении удоя молока составит 0,296 руб. за 1 кг.