Реферат: Коллоидная химия

Содержание

I. Раздел «Молекулярно – кинетические свойства коллоидных систем»

II. Раздел «Оптические свойства коллоидных систем»

III. Раздел «Структурно – механические свойства дисперсных систем»

IV. Раздел «Растворы ВМС»

V. Раздел «Представители гетерогенно – дисперсных систем»

Литература

I. Раздел «Молекулярно – кинетические свойства коллоидных систем»

1. Молекулярно – кинетические свойства коллоидов. Броуновское движение

Молекулярно-кинетические свойства коллоидных систем и растворов ВМС, как и газов, и молекулярных или ионных растворов, обнаруживаются в таких явлениях, как броуновское движение, диффузия, осмотическое давление. Частицы ультрамикрогетерогенных систем (золей, аэрозолей) участвуют в тепловом движении и подчиняются всем молекулярно-кинетическим законам. Благодаря этому можно экспериментально определить размер, массу и концентрацию частиц дисперсной фазы.

Броуновское движение (название дано в честь английского ботаника Броуна, обнаружившего с помощью микроскопа непрерывное движение мелких частичек цветочной пыльцы, взвешенных в воде) проявляется в хаотическом и непрерывном движении частиц дисперсной фазы под действием ударов молекул растворителя (дисперсионной среды), находящихся в состоянии интенсивного теплового движения. В зависимости от размера частиц их движение может быть различным.

Частицы коллоидной степени дисперсности, испытывая с разных сторон многочисленные удары молекул жидкости, могут перемещаться поступательно в самых разнообразных направлениях. Если частица имеет сравнительно большой размер, то число ударов велико, и по соответствующему закону статистики результирующий импульс становится равным нулю, такая частица не может двигаться под действием теплового движения молекул.

Кроме того, частицы с большой массой обладают инерционностью и малочувствительны к ударам молекул. Очень малые частицы имеют значительно меньшие массу и поверхность. На такую частицу будет приходиться существенно меньшее число ударов, поэтому вероятность неравномерного распределения импульсов, получаемых с разных сторон, увеличивается. Это происходит как вследствие неодинакового числа ударов с разных сторон частицы, так и вследствие различной энергии молекул, сталкивающих с частицей. В зависимости от размеров частица приобретает колебательное, вращательное и поступательное движение.

Таким образом, броуновское движение является следствием теплового движения в дисперсионной среде и прямым отражением статистики.

Броуновское движение – следствие случайных микроотклонений (флуктуаций), эффект которых возрастает с уменьшением размеров системы, и наглядное проявление отклонений от второго закона термодинамики в микросистемах, т.е. подтверждение его статистического характера.

2.Осмотическое давление. Уравнение Вант-Гоффа

Осмотическое давление в растворе или золе описывается следующим строгим термодинамическим соотношением:

(1)

где - разность между химическими потенциалами растворителя при установлении равновесия относительно полунепроницаемой мембраны; - средний парциальный мольный объем растворителя; - активность растворителя в растворе.

В уравнении (1) можно активность заменить мольными долями

(2)

где - мольная доля растворителя и дисперсной фазы соответственно; - рациональный осмотический коэффициент.

Если золь разбавлен, то разложив в ряд логарифм, ограничившись первым членом ряда и использовав равенство, получим уравнение Вант-Гоффа:

(3)

где - массовая концентрация; - молекулярная масса частицы.

Осмотическое давление дисперсной системы определяется только численной концентрацией и зависит от природы и размера частиц. Малое осмотическое давление коллоидной системы объясняется благодаря большой массе коллоидных частиц при одной и той жен весовой концентрации численная концентрация коллоидной системы всегда значительно меньше, чем у истинного раствора.

Вторая особенность осмотического давления лиозолей – его непостоянство – объясняется явлением агрегации, характерным для коллоидных систем.

Малое значение и непостоянство осмотического давления лиозолей являются причиной того, что осмометрия, а также криоскопия и эбуллиоскопия не применяются для определения численной концентрации или размера коллоидных систем.

3. Диффузия. Ее практическое значение. Уравнение Эйнштейна. Связь между средним сдвигом и коэффициентом диффузии. Уравнение Фика

Диффузией называют самопроизвольный процесс выравнивания концентрации частиц по всему объему раствора или газа под влиянием броуновского движения.

Процесс диффузии идет самопроизвольно, поскольку он сопровождается увеличением энтропии системы. Равномерное распределение вещества в системе отвечает наиболее вероятному ее состоянию.

Часто за причину диффузии принимают осмотическое давление. Это представление было развито Нернстом (1885 г.). Так как осмотическое давление может проявляться лишь при наличии полунепроницаемой перегородки, то это давление бессмысленно рассматривать как какую-то реальную силу, существующую вне связи с мембраной. Тем не менее, осмотическое давление, являющееся также результатом хаотического движения молекул, иногда удобно принимать за причину диффузии.

Перенос массы в результате диффузии сходен с закономерностями переноса тепла или электричества – это легло в основу первого закона диффузии (Фик, 1855г.).

где - количество про диффундировавшего вещества;

- коэффициент диффузии, зависящий от свойств диффундирующих частиц и среды;

- градиент концентрации;

- площадь, через которую идет диффузия;

- продолжительность диффузии.

Знак минус перед правой частью уравнения, так как с увеличением значений величина уменьшается. Уравнение можно представит в виде:

где - удельный поток диффузии, характеризующий количество вещества, переносимое за единицу времени через единицу площади.

Принимая отсюда , т.е. коэффициент диффузии численно равен количеству вещества, про диффундировавшего через единицу площади в единицу времени.

Это уравнение Эйнштейна. Для частиц, по форме близких к сферическим, .

где - масса 1 моля вещества.

Так как существует связь между броуновским движением и диффузией, то должна существовать связь между средним квадратичным значением проекции смещения частицы и коэффициентом диффузии . Эта связь была установлена Эйнштейном (1905г.) и независимо от него Смолуховским (1906 г.):

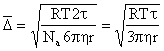Пользуясь уравнением Эйнштейна-Смолуховского и, зная и всех величин, можно вычислить число Авогадро.

Теория броуновского движения, созданная Эйнштейном и Смолуховским, подтвердила реальное существование молекул. Исследование броуновского движения привело к созданию теории флуктуации и способствовало развитию статической физики.

Флуктуации представляют собой спонтанные отклонения какого-нибудь параметра от среднего равновесного значения в достаточно малых объемах системы. Флуктуация представляет собой явление как бы обратное явлению диффузии.

4. Гипсометрический закон Лапласа

Уравнение Лапласа носит название гипсометрического закона.

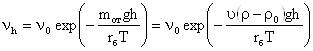Этот закон был экспериментально подтвержден Перреном (1910г.). Изучая распределение монодисперсной суспензии гуммигута, он использовал уравнение Лапласа для определения числа Авогадро, которое оказалось равным 6,82*1023 (точное значение 6,024*1023). Гипсометрический закон соблюдается и в аэрозолях, частицы которых имеют небольшую плотность и размер не более 0,05мкм.

Этому закону подчиняется распределение газа по высоте:

С помощью этой формулы удобно вычислять для любой свободнодисперсной системы величину , представляющую собой высоту, на которую надо подняться, чтобы численная концентрация уменьшилась с до .

5 Кинетическая или седиментационная устойчивость коллоидно-дисперсных систем. Седиментационый анализ. Вывод уравнения радиуса частиц. Кривые распределения. Монодисперсность и полидисперсность. Методы седиментационного анализа (в поле земного тяготения, в поле центробежной силы – центрифугирование). Их практическое значение

Способность дисперсной системы сохранять равномерное распределение частиц по всему объему принято называть седиментационной, или кинетической устойчивостью системы.

Принцип седиментационного метода анализа дисперсности состоит в измерении скорости осаждения частиц, обычно в жидкой среде. По скорости осаждения частиц с помощью соответствующих уравнений рассчитывают размеры частиц.

Метод позволяет определить распределение частиц по размерам и соответственно подсчитать их удельную поверхность.

Размер частицы дисперсной фазы обычно характеризуют радиусом частицы, реже объемом или площадью ее поверхности. Радиус однозначно определяется только для частиц сферической формы.

В монодисперсной системе все частицы осаждаются с одинаковой скоростью. В соответствии с этим такую же скорость перемещения имеет граница осветления, концентрация частиц по уменьшающейся высоте столба суспензии сохраняется постоянной и также с постоянной скоростью увеличивается масса осевших частиц. Если - общая масса дисперсной фазы, - первоначальная высота столба суспензии, то - масса дисперсной фазы в объеме, приходящаяся на единицу высоты столба суспензии. При скорости осаждения частиц в течение времени вещество осядет из столба высотой , и масса осевшего вещества составит

, (1)

Это уравнение описывает кинетику седиментации в монодисперсной системе. Если принять, что частицы имеют сферическую форму и при их осаждении соблюдается закон Стокса, то, используя формулу:

, (2)

получим:

, (3)

Отсюда радиус частицы равен

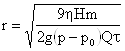, (4)

Следовательно, определяя экспериментально зависимость массы осевшего осадка от времени, можно рассчитать размер частиц.

Определение дисперсного состава суспензий, порошков, аэрозолей и других микрогетерогенных систем основано на разнообразных седиментометрических методах дисперсионного анализа.

К ним относят: отмучивание – разделение суспензии на фракции путем многократного отстаивания и сливания; измерение плотности столба суспензии, изменяющейся вследствие седиментации частиц суспензии; пофракционное (дробное) оседание; метод отбора массовых проб – один из наиболее достоверных; накопление осадка на чашке весов; электрофотоседиментометрия, основанная на изменении интенсивности пучка света, проходящего через столб суспензии, о чем судят по измерениям оптической плотности; седиментометрия в поле центробежных сил, основанная на применении центрифуг.

Для успешного проведения седиментометрического анализа должно выполняться условие независимого движения каждой частицы. Этого достигают, применяя разбавленные системы, а в некоторых случаях добавляя стабилизаторы, препятствующие слипанию частиц.

Известны и применяются в практике различные приборы – седиментометры. Например, ряд приборов позволяет проводить анализ по методу накопления осадка на чашечке весов (метод предложен Оденом). Принцип метода состоит в том, что через определенные интервалы времени взвешивают чашку, опущенную в суспензию, и по нарастанию ее массы судят о соотношении различных фракций в суспензии.

Широкое применение для взвешивания чашки с осадком получили торсионные весы. Проведение седиментометрического анализа основано на том, что по мере оседания частиц их масса на чашке увеличивается вначале быстро, так как, прежде всего, оседают наиболее тяжелые частицы, затем все медленнее. При этом каждая фракция считается монодисперсной.

По данным взвешивания осадка получают кривую седиментации, которая выражает зависимость количества осадка q от времени осаждения . Для монодисперсной системы (рис. 1, а) угол наклона прямолинейного участка кривой определяется скоростью оседания частиц и связан с их размером.

Точка перегиба позволяет определить время полного оседания суспензии 1, которое в свою очередь, дает возможность найти скорость оседания частиц , где h – высота столба суспензии над чашкой весов.

Для бидисперсной системы седиментационная кривая имеет более сложный вид (рис. 1, б). Можно представить себе, что частицы каждой из двух фракций, выпадающие с постоянной скоростью, дают две прямых OA и OB, с различными угловыми коэффициентами, в соответствии с размерами частиц и концентрацией каждой фракции. Однако при совместном оседании обеих фракций мы наблюдаем не эти прямые в отдельности, а суммарную линию седиментации, тангенс угла наклона которой к оси абсцисс является суммой тангенсов углов наклона обеих прямых (OA и OB). В момент полного выпадения фракции, состоящей из частиц больших размеров, эта суммарная линия получает излом (в точке A/) и далее идет параллельно прямой OB, выражающей скорость оседания частиц фракции меньших размеров. В момент окончания оседания второй фракции на графике в точке B/ обнаруживается второй излом, после которого прямая идет параллельно оси абсцисс.

По кривой седиментации оказывается возможным построить прямые осаждения для каждой фракции в отдельности, которые, как было уже сказано, не могут быть получены непосредственно на опыте.

Из рис. 1, б видно, что, продолжая отрезок A/B/ линии седиментации до пересечения с осью ординат и проводя из точки пересечения y прямую, параллельную оси абсцисс, до пересечения ее с линией A/A// , мы получим конечную точку A прямой осаждения фракции, состоящей из крупных частиц. Проводя из начала координат линию OB, параллельную линии y B/ , до пересечения с линией B/B// , получим прямую осаждения фракции, состоящей из мелких частиц, с конечной точкой B .

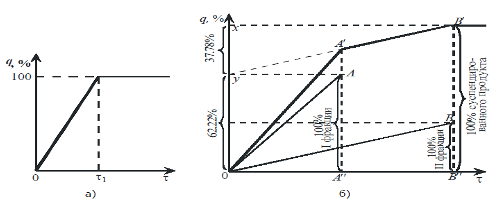
Рис.1 Кривые седиментации монодисперсной (а) и полидисперсных (б, в) систем.

Если ординаты конечных точек A и B прямых осаждения обеих фракций выражают общее количество (по массе) этих фракций, то очевидно, что ордината точки B/ суммарной линии выражает общее количество обеих фракций (100 %) суспендированного вещества. Легко понять, что отрезки Oy и yx дают относительное содержание каждой фракции в процентах от общего количества суспендированного вещества.

Имеются графические и аналитические методы расчета кривой седиментации.

Монодисперсная система – это система, которая состоит из одинаковых по размеру частиц.

Полидисперсная система – это система, частицы которой имеют различные радиусы.

Так как коллоидные частицы под действием силы тяжести не седиментируют, то под действием центрифуги с большим ускорением можно заставить оседать достаточно быстро и коллоидные частицы.

Ультрацентрифугу используют для определения размера частиц.

6. Методы очистки золей: диализ, электродиализ, ультрафильтрация

Диализ. Очищаемый золь, заливают в сосуд, дном которого служит мембрана, задерживающая коллоидные частицы или макромолекулы и пропускающая молекулы растворителя и низкомолекулярные примеси. Внешней средой, контактирующей с мембраной, является растворитель. Низкомолекулярные примеси, концентрация которых в золе или макромолекулярном растворе выше, переходят сквозь мембрану во внешнюю среду (диализат). Очистка идет до тех пор, пока концентрации примесей в золе и диализате не станут близкими по величине. Если обновлять растворитель, то можно практически полностью избавиться от примесей.

Такое использование диализа целесообразно, когда цель очистки – удаление всех низкомолекулярных веществ, проходящих сквозь мембрану. Однако в ряде случаев задача может оказаться сложнее – необходимо освободиться только от определенной части низкомолекулярных соединений в системе. Тогда в качестве внешней среды применяют раствор тех веществ, которые необходимо сохранить в системе. Именно такая задача ставится при очистке крови от низкомолекулярных шлаков и токсинов (солей, мочевины и т.п.). Если удалять подряд все низкомолекулярные компоненты крови, то начинается разрушение клеток, что, в свою очередь, может привести к гибели организма.

Электродиализ. Очистку от электролитов можно значительно ускорить действием приложенной разности потенциалов (электромиграцией). Такой метод очистки называется электродиализом. Его используют для очистки различных биологических объектов (растворы белков, сыворотка крови и пр.).

Ультрафильтрация. Ультрафильтрация – метод очистки коллоидных систем путем продавливания дисперсионной среды вместе с низкомолекулярными примесями через ультрафильтры. Ультрафильтрами служат мембраны того же типа, что и для диализа. В мешочек из ультрафильтра наливают очищаемый золь или раствор высокомолекулярного вещества. К золю прилагают давление, избыточное по сравнению с атмосферным. Дисперсионную среду обновляют, добавляя к золю чистый растворитель.

Ультрафильтрация используется не только для удаления низкомолекулярных компонентов смеси, но и для концентрирования систем и разделения веществ с различной молекулярной массой. Этим методом очищают сточные воды, отделяют культуральные жидкости от продуктов микробиологического синтеза, концентрируют биологически активные вещества: белки, ферменты, антибиотики и т.д.

В последние годы ультрафильтрация наряду с диализом получила распространение в клинике для обработки крови. Этот метод применяется для выведения из организма токсических веществ и, если это необходимо, для удаления избытка жидкости.

II. Раздел «Оптические свойства коллоидных систем»

1. Оптические свойства коллоидных систем. Опалесценция и флуоресценция

Прохождение света через коллоидную систему вызывает три оптических эффекта: поглощение, отражение и рассеивание лучей. Поглощение свойственно всем системам, тогда как отражение более характерно для грубодисперсных систем (эмульсий и суспензий), где размер частиц больше, чем длина волны облучения. Поэтому, в отличие от молекулярных и ионных растворов, которые не имеют поверхности раздела фаз и оптически однородны, коллоидные растворы рассеивают свет.

Это проявляется опалесценцией в виде голубоватого матового свечения при освещении боковым светом. При пропускании параллельного пучка света через коллоидный раствор наблюдается конус рассеянного света – эффект Тиндаля. По способности рассеивать свет можно определять концентрацию коллоидных частиц в растворе - метод нефелометрии.

Опалесценция (светорассеяние) наблюдается только тогда, когда длина световой волны больше размера частицы дисперсной фазы. Если длина световой волны много меньше диаметра частицы, происходит отражение света, проявляющееся в мутности.

Рассеянный свет имеет ту особенность, что он распространяется во всех направлениях. Интенсивность рассеянного света в различных направлениях различна.

С опалесценцией внешне сходна, флуоресценция, характерная для истинных растворов некоторых красителей. Она заключается в том, что раствор при наблюдении в отраженном свете имеет иную окраску, чем в проходящем, и в нем можно видеть такой же конус Тиндаля, что и в типичных коллоидных системах. Однако по существу это совершенно различные явления. Опалесценция возникает в результате рассеяния света, при этом длина волны рассеянного света та же, что и падающего. Флуоресценция же представляет собой внутримолекулярное явление, заключающееся в селективном поглощении молекулой вещества светового луча и в трансформировании его в световой луч с другой, большей длиной волны.

2. Поглощение света дисперсными системами. Зависимость поглощения от концентрации. Закон Бугера-Ламберта-Бера

В 1760г. Ламберт, а еще ранее Бугер установили следующую зависимость между интенсивностью прошедшего света и толщиной среды, через которую этот свет прошел:

где - интенсивность прошедшего света;

- интенсивность падающего света;

- коэффициент поглощения;

- толщина поглощающего света.

Согласно закону Бугера-Ламберта – каждый последующий слой поглощает ту же долю проходящего света, что и предыдущий.

Бер показал, что коэффициент поглощения растворов с абсолютно бесцветным и прозрачным растворителем пропорционален молярной концентрации растворенного вещества: .

Вводя значение молярного коэффициента поглощения в уравнение Бугера-Ламберта, получим закон Бугера-Ламберта-Бера:

Закон устанавливает зависимость интенсивности прошедшего света от толщины слоя и концентрации растворенного вещества.

Логарифмируя уравнение, получим:

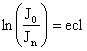где - оптическая плотность раствора ;

- светопропускание раствора.

Если , тогда ,

Если , раствор не адсорбирует света, тогда закон Бугера-Ламберта-Бера имеет вид:

т.е. интенсивность прошедшего света будет равна интенсивности падающего.

Молярный коэффициент поглощения зависит от длины волны адсорбирующего света, температуры и природы растворенного вещества и растворителя и не зависит от концентрации раствора.

Закон Бугера-Ламберта-Бера приложим для золей высокой дисперсности, если слой жидкости не слишком толст, а концентрация раствора не слишком большая.

Для металлических золей уравнение светопоглощения должно учитывать дисперсность системы:

3. Рассеяние света коллоидными системами. Конус Тиндаля. Закон Релея и его анализ

Тиндаль (1869г.) наблюдал образование светящегося конуса при пропускании пучка света через коллоидный раствор.

Светорассеивание наблюдается только тогда, когда длина световой волны больше размера частицы дисперсной фазы. Если длина световой волны много меньше диаметра частицы, происходит отражение света, проявляющиеся в мутности, заметной визуально.

Все коллоидные растворы способны рассеивать свет (опалесцировать). Опалесценция становится особенно заметной, если через раствор пропускать пучок сходящихся лучей, поставив между источником света и кюветой с раствором линзу. При этих условиях в коллоидном растворе, наблюдаемом сбоку, виден ярко светящийся конус (конус Тиндаля).

Релей вывел уравнение, связывающее интенсивность падающего света с интенсивностью света, рассеянного единицей объема системы .

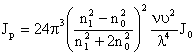где - показатели преломления дисперсной фазы и дисперсной среды;

- численная концентрация;

- объем одной частицы;

- длина световой волны.

Уравнение Релея применимо для частиц, размер которых составляет не более 0,1 длины световой волны. Для частиц большего размера изменяется обратно пропорционально не четвертой, а меньшей степени .

Когда частицы становятся настолько велики, что их размер значительно превышает , светорассеивание переходит в отражение света, не зависящее от длины световой волны.

Из уравнения Релея можно сделать следующие выводы:

· Для частиц данного размера интенсивность рассеянного света прямо пропорциональна концентрации золя.

· Интенсивность рассеянного света пропорциональна квадрату объема частицы или для сферических частиц шестой степени их радиуса.

· При опалесценции под действием белого света при боковом освещении бесцветные коллоидные системы обнаруживают синеватую окраску.

· Опалесценция золей интенсивнее, чем растворов ВМС из-за большей плотности.

· Опалесценция истинных растворов весьма незначительна, т.к. вследствие малого объема частиц выражение в численном уравнение Релея очень велико.

4. Оптические методы исследования: нефелометрия, ультрамикроскопия, турбидиметрия, электронная микроскопия

В нефелометрии измеряется интенсивность света, рассеянного дисперсной системой. Вместо измерения абсолютных значений рассеянного света на практике проводят сравнение интенсивностей лучей, рассеянных стандартным и исследуемым золем. На рис. 2,а приведена схема визуального нефелометра Кляйнмана (нефелометры иногда называют тиндалеметрами). При измерении подниманием или опусканием экранов изменяют высоту осветленной части пробирок с золями, добиваясь одинаковой осветленности в обеих половинах окуляра. При подчинении исследуемой монодисперсной системы уравнению Рэлея для интенсивности рассеянного света можно записать

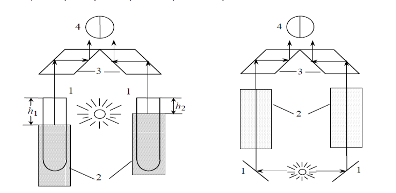
Рис.2 Схема нефелометра -а Схема турбидиметра - б

а - 1 – зеркала, 2 – кюветы, 3 – призмы, 4 – окуляр.

б - 1 – пробирки с золями, 2 - экраны, 3 –призмы, 4 – окуляр

В турбидиметрии измеряют интенсивность света, прошедшего через стандартную и исследуемую дисперсную систему. Схема визуального турбидиметра приведена на рис. 2,б. Оптическая плотность раствора пропорциональна концентрации и объему частиц дисперсной фазы

D = k′cV .

При одинаковой осветленности поля зрения в окуляре имеем равенство cстандVстанд = cхVх, применение, которого аналогично рассмотренному для нефелометрии.

Ультрамикроскопия и электронная микроскопия.

Коллоидные частицы нельзя наблюдать в обычном микроскопе, так как их размеры меньше разрешающей способности микроскопа. Для средней части видимой области спектра можно достигнуть разрешающей способности не выше, чем 0,2 мкм. Ультрафиолетовый свет, специальная кварцевая оптика и фотографическая регистрация позволяют увеличить разрешающую способность и довести ее до 0,1 мкм, что является верхней границей коллоидной дисперсности. Р. Зидентопф и Р. Зигмонди в 1903 г. предложили так называемый ультрамикроскопический метод исследования коллоидных систем. Они применили сильное боковое освещение наблюдаемого под микроскопом раствора таким образом, чтобы свет не попадал в объектив микроскопа. При этом коллоидные частицы были видны как отдельные светлые точки, что позволяет установить их присутствие в растворе и наблюдать за их движением.

При ультрамикроскопическом наблюдении можно судить о том, в какой степени коллоидные частицы сферически симметричны. Свет, рассеиваемый сферическими частицами, имеет постоянную интенсивность при их движении в растворе. Если частицы не сферичны, а имеют, например, палочкообразную или пластинчатую форму, то при движении они мерцают.

В электронной микроскопии используется поток быстрых электронов с длиной волны до 10-9 м, что дает очень высокое разрешение, соответствующее увеличению до 105. Метод дает сведения о размерах и форме частиц, макромолекул и надмолекулярных образований. Электронная микроскопия существенно дополняет ультрамикроскопию. Электронный микроскоп позволяет увидеть мельчайшие частички и многие особенности их строения, но необходимость работы в высоком вакууме требует удаления жидкой дисперсионной среды.

III. Раздел «Структурно – механические свойства дисперсных систем»

1. Структурирование в коллоидных и полимерных системах. Гели и студни. Их свойства, механизм образования и практическое значение. Тиксотропия и синтерезис

Согласно А.И. Рабинерсону и Г.И. Фуксу, структуры, образующиеся в высокодисперсных системах, можно классифицировать по их плотности:

1. Пространственные – структуры характерны для дисперсных систем с анизодиаметрическими частицами;

2. Компактные – структуры часто возникают в системах с изодиаметрическими частицами.

При истинной коагуляции, когда частицы полностью теряют фактор устойчивости, они слипаются друг с другом, образуя компонентные агрегаты. Достигнув определенного размера, эти агрегаты образуют плотный коагулят. Если же происходит неполная астабилизация системы, то фактор устойчивости будет снят только с некоторых участков поверхности частиц, да ито не полностью, и в результате этого частицы, слипаясь по таким местам, образуют пространственную сетку, в петлях которой находится дисперсная среда. Происходит гелеобразование.

Гелеобразованием называют переход коллоидного раствора из свободнодисперсного состояния (золя) в связомодисперсионное состояние (гель).

На гелеобразование влияет ряд факторов:

· концентрация дисперсной среды;

· уменьшение размера частиц;

· температура;

· механическое воздействие.

Аналогичный переход раствора ВМС в студень называется застудневанием. Оно может происходить спонтанно, в результате изменения температуры при концентрировании раствора или при добавлении к нему не слишком большого количества электролита.

Студни обладают такими свойствами как вязкость, осмотическое давление, эластичность, текучесть, особенность рассеивать свет, тиксотропные свойства, синтерезис.

Тиксотропия – способность структур после их разрушения в результате какого-нибудь механического воздействия самопроизвольно восстанавливаться во времени.

Синтерезис - самопроизвольное уменьшение размеров геля с одновременным выделением из него дисперсной среды, содержащейся в петлях геля.

Студни и процесс застудневания имеют большое значение в медицине, биологии, техники, хлебопекарной промышленности. Образование клеевого слоя при склеивании, желатировании пироксилина, получение искусственного волокна, дубление кожи.

2. Коагуляционные и конденсационно–кристаллизационные структуры по П.А. Ребиндеру

Согласно Ребиндеру, структуры в коллоидных и микрогетерогенных системах можно разделить на:

· коагуляционные (тиксотропно-обратимые) – структуры, возникающие в результате понижения агрегативной устойчивости дисперсных систем, когда частицы полностью теряют фактор устойчивости, они слипаются друг с другом, образуя компактные агрегаты.

· конденсационно-кристаллизационные (необратимые - разрушаюшиеся структуры) – связи между частицами образованы за счет химических сил. Эти структуры возникают либо в результате образования прочных химических связей между частицами, либо вследствие сращивания кристалликов в процессе выкристаллизовывания новой фазы.

3 Нормальные ньютоновские жидкости, структурированные жидкости. Вязкость. Аномалия вязкости. Уравнение Ньютона, Пуазейля, Бингама. Реологические зависимости. Уравнения Эйнштейна для определения вязкости коллоидных систем

Жидкообразные тела классифицируют на:

1. ньютоновские жидкости – системы, вязкость которых не зависит от напряжения сдвига и является постоянной величиной в соответствии с законом Ньютона;

2. структурированные – течение которых не следует закону Ньютона, их вязкость зависит от напряжения сдвига;

2.1 стационарные – реологические свойства которых не изменяются со временем;

2.2 нестационарные – для которых эти характеристики зависят от времени.

Вязкость – способность жидкого вещества оказывать сопротивление движению. В жидкостях вязкость обусловлена внутренним давлением и с повышением температуры вязкость понижается. В газах вязкость обусловлена тепловым движением молекул, с повышением температуры вязкость возрастает.

Коэффициент вязкости представляет собой силу сопротивления , которая возникает между слоями текучего тела с поверхностями площадью и удаленными друг от друга на расстояние при перемещении их относительно друг друга со скоростью .

- динамическая вязкость

Свойства вещества, противоположные вязкости, называется текучестью, а величину противоположная коэффициенту вязкости коэффициент вязкости.

Кинематическая вязкость учитывает плотность вещества и связана с динамической вязкостью:

Жидкости способные течь, но не подчиняющиеся закону Ньютона, принято называть аномальными.

По определению вязкости, данному Ньютоном, сила внутреннего трения , равная по значению, но обратная по направлению приложенной извне силе, пропорциональная площади слоя , к которому приложена эта сила, и градиенту скорости движения между слоями:

Относя силу к площади, тогда уравнение будет выглядеть так:

где - напряжение сдвига, поддерживающее течение жидкости.

Ламинарное течение жидкости по трубкам описывается уравнением Пуазейля:

где - объемная скорость истечения;

- радиус и длина трубки;

- разность давлений на концах трубки;

- вязкость жидкости.

Бингам выразил пластическую вязкость уравнением:

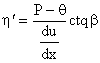где - угол, образуемый прямой с осью абцисс.

Однако для большинства структурированных коллоидных систем зависимость от выражается не прямой, а кривой.

Причина такого явления заключается в том, что при достижении предела текучести структура разрушается не сразу, а постепенно по мере увеличения градиента скорости жидкости.

Различают три критических напряжения сдвига:

1. - первый, или минимальный, предел текучести, соответствующий началу течения.

2. - предел текучести по Бингаму, отвечающий отрезку на оси абсцисс, отсекаемому продолжением прямолинейного участка кривой.

3. - максимальный предел текучести, соответствующий значению , при которой кривая переходит в прямую линию.

Первая аксиома реологии: при всестороннем равномерном сжатии материальные системы ведут себя одинаково – как идеальные упругие тела.

Вторая аксиома реологии: любая материальная система обладает всеми реологическими свойствами.

Эйнштейном была установлена связь между вязкостью дисперсной системы и объемной долей дисперсной фазы :

где - вязкость дисперсной среды.

Была установлено, что коэффициент при зависит от формы частиц, поэтому уравнению Эйнштейна можно придать более общий вид:

где - коэффициент, зависящий от формы частицы дисперсной фазы.

Для относительной и удельной вязкости дисперсной системы уравнение Эйнштейна переходит в следующие соотношения:

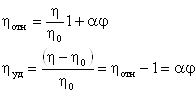
IV. Раздел «Растворы ВМС»

1. Особенности строения полимеров. Причины гибкости макромолекул. Образование ассоциатов

Высокомолекулярными соединениями называют вещества, имеющие относительную молекулярную массу приблизительно от 10000 до нескольких миллионов. ВМС, состоящие из большого числа повторяющихся одинаковых звеньев, называются полимерами.

Молекулы полимеров могут быть линейными и разветвленными. Именно линейные формы макромолекул определяют типичные свойства полимеров: каучукоподобная эластичность, способность образовывать прочностные пленки и нити, набухать, давать при растворении вязкие растворы.

Разветвление у макромолекул сильно влияет на их гибкость. Короткие и часто расположенные боковые цепи увеличивают жесткость молекул. На гибкость макромолекулы могут влиять молекулы растворителя или пластификаторы.

Гибкость углеводородной цепи обуславливается вращением одних участков цепи относительно других вокруг одинаковой валентной связи, соединяющей соседние атомы углерода. Так как таких отдельных связей в макромолекуле множество, то становится понятной та исключительная гибкость, которой обладают углеводородные цепочки. Молекулы полимеров не связанные друг с другом и ведут себя вполне самостоятельно, когда они находятся в относительно разбавленных растворах. В концентрированных растворах, когда вероятность столкновения молекул растворенного вещества велика, макромолекулы могут взаимодействовать и образовывать ассоциаты.

Ассоциаты в разбавленных растворах полимеров не являются постоянно существующими образованиями и не имеют определенного состава. Ассоциаты образуются и в растворах НМС за счет столкновения двух, трех, четырех и более молекул. Особенностью образования ассоциатов в растворах ВМС является то, что длинные и гибкие макромолекулы могут входить отдельными своими участками в состав различных ассоциатов.

2. Общие и отличительные свойства растворов высокомолекулярных соединений (ВМС) и золей

Растворы ВМС представляют собой истинные растворы, термодинамически устойчивые и обратимые, не нуждающиеся в стабилизаторе частицы, содержащиеся в таких растворах, состоят не из множеств малых молекул, как это имеет место у коллоидов, и представляют отдельные молекулы относительно очень больших размеров. В этом и заключается отличие растворов ВМС от растворов низкомолекулярных соединений.

Растворы ВМС в плохих растворителях содержат молекулы свернутые в компактный клубок с явно выраженной межфазной поверхностью.

Они представляют отдельную фазу. Такие растворы ВМС можно отнести к коллоидным системам. Растворы ВМС благодаря большим размерам их молекул обладают рядом свойств лиозолей, что позволяет рассматривать многие проблемы одновременно и для коллоидных растворов и для растворов ВМС.

В отличие от золей, для растворов ВМС характерны большая вязкость, высокая устойчивость, способность к набуханию.

Золи могут существовать в газообразном состоянии (аэрозоли), а ВМС – нет, т.к. произойдет разрыв макромолекулы.

3. Набухание. Стадии процесса набухания. Факторы, влияющие на набухание. Кинетика набухания. Степень набухания. Ограниченное и неограниченное набухание. Давление набухания. Концентрация

Растворение высокомолекулярных соединений с линейными гибкими молекулами в отличие от растворения НМС сопровождается набуханием.

При набухании высокомолекулярных соединений поглощает низкомолекулярный растворитель, значительно увеличивается в массе, при этом изменяет механические свойства без потери однородности. Объем ВМС может увеличиваться при набухании до 1000 – 1500%.

На первой стадии набухания происходит сольватация макромолекул в результате диффузии растворителя в высокомолекулярное вещество. Эта стадия характеризуется выделением тепла и упорядочением расположения молекул растворителя около макромолекулы, в результате чего энтропия системы в первой стадии растворения обычно даже понижается. Основное значение этой стадии при растворении сводится к разрушению связей между отдельными макромолекулами, следствии чего они становятся свободными.

Второй стадией является набухание или растворение, обусловленное чисто энтропийными причинами. В этой стадии, поскольку сольватация уже завершилась, тепловой эффект равен нулю или имеет отрицательное значение, а энтропия резко возрастает. Вторую стадию растворения можно рассматривать как чисто осмотический процесс. Легче всего набухают полимеры в вязкотекучем и высокоэластичном состоянии.

К факторам, влияющим на набухание, относятся: термодинамическая активность растворителя, температура, физическое состояние полимера, природа полимера и растворителя. Типичные кинетические кривые набухания, характеризующие зависимость растворителя, представлены на рисунке.

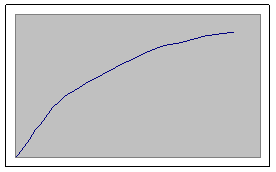
Кинетические кривые для ограниченного набухания представляют аналитически:

где - константа скорости набухания; - степень набухания при достижении равновесия и ко времени соответственно.

Проинтегрировав, получим уравнение кинетики набухания, подобное уравнению для кинетики ленгмюровской адсорбции:

Набухание полимера в жидкости характеризуется степенью набухания , вычисляемой по формуле:

где - навеска полимера до и после набухания.

Набухание не всегда заканчивается растворением. Очень часто после достижения известной степени набухания процесс прекращается.

Причины ограниченного набухания:

1. ВМС и растворитель способны смешиваться ограниченно. Поэтому в результате набухания в системе образуется две фазы – насыщенный раствор полимера в растворителе и насыщенный раствор растворителя в полимере (гель, студень). Такое ограниченное набухание носит равновесный характер.

2. Между молекулами полимера существуют поперечные химические связи, и вещество по существу представляет собой пространственную сетку.

Неограниченное набухание это, когда полимер растворяется в растворителе. Набухание ВМС может прийти к возникновению значительного давления, если что-то препятствует увеличению объема образца (набухание древесины в воде).

Давление набухания зависит от степени поперечной связанности полимера, что достаточно проявляется лишь при достаточной большой степени набухания. Давление набухания аналогично осмотическому давлению и определяется по уравнению:

где - парциальный мольный объем растворителя;

- активность растворителя;

- давление насыщенного пара растворителя соответственно над набухшим полимером и чистым растворителем.

Контракция – уменьшение объема системы при набухании вещества в растворителе. Зависимость контракции от степени набухания:

где - константы, зависящие от природы набухающего вещества и растворителя.

Контракция объясняется взаимодействием (сальватацией) вещества с растворителем, при котором происходит уплотнение системы.

4. Термодинамика растворения ВМС

Процесс растворения ВМС рассматривают как процесс смешения двух жидкостей. ВМС с гибкими макромолекулами должны лучше растворяться, чем с жидкими, поскольку первые могут располагаться в растворе большим числом способов. У жестких макромолекул энергия взаимодействия между отдельными макромолекулами цепочка очень велика, и такие цепи трудно оторвать друг от друга.

Самопроизвольное растворение ВМС сопровождается уменьшением изобарно-изотермического потенциала, согласно второму закону термодинамики:

Когда система не изменяет своего объема:

При самопроизвольном растворении полимера . Это может быть в двух случаях:

1. если , т.е. при растворении выделяется тепло;

2. если , так как некоторые полимеры способны растворяться с поглощением тепла.

5. Особенности осмотического давления и вязкости у растворов ВМС

Осмотическое давление растворов полимеров значительно выше, чем у НМС и не подчиняется закону Вант-Гоффа. Объясняется это тем, что макромолекула благодаря гибкости ведет себя в растворе как несколько коротких молекул. Осмотическое давление увеличивается прямо пропорционально концентрации.

На основании представлений Галлера для описания зависимости осмотического давления от концентрации полимеров было предложено уравнение:

где - второй вириальный коэффициент;

- константа, характеризующая отклонения от уравнения Вант-Гоффа, зависящая от природы растворителя и растворенного вещества, но не зависящее от молекулярного веса растворенного вещества.

Вязкость растворов, содержащих макромолекулы, обычно выше вязкости растворов НМС и коллоидных растворов тех же концентраций.

Отклонения вязкости растворов ВМС от законов, которым подчиняются растворы НМС, следует объяснить особенностями гидродинамики систем, содержащих вытянутые и гибкие макромолекулы и наличием в них ассоциатов и легко разрушаемых структур.

6. Определение молекулярной массы по вязкости их растворов

Приведенная вязкость растворов одного и того же полимера обычно возрастает с повышением концентрации, причем это возрастание в интервале небольших концентраций происходит по прямой.

Отрезок, отсекаемый этой прямой отвечает величине характеристической вязкости , отражающей гидродинамическое сопротивление потоку молекул данного полимера. Характеристическая вязкость представляет собой приведенную вязкость при бесконечно большом разбавлении раствора.

В настоящее время для определения молекулярного веса предложено уравнение, учитывающее взаимодействие макромолекул даже в разбавленных растворах и изменение константы с длиной молекулы:

где - коэффициент постоянный для растворов полимергомологического ряда в данном растворителе;

- величина, характеризующая форму макромолекул в растворе и связанная с гибкостью цепи.

7. Полиэлектролиты и их свойства

Полиэлектролиты – это ВМС, молекулы которых содержат гомогенные группы и в растворах способны распадаться на ионы. По природе содержащихся в них ионогенных групп можно разделить на три категории:

1. полиэлектролиты, содержащие кислотную группу . Первую группу содержат гуммиарабик, альгинаты, растворимый крахмал, а вторую – агар.

2. полиэлектролиты, содержащие основную группу . Такие вещества в природе не встречаются, но могут быть синтезированы.

3. полиэлектролиты, содержащие одновременно как кислотную, так и основную группу (полиамфолиты). К ним относятся белки, синтетические полиамфолиты – сополимеры акриловой кислоты и винилпиридина, глютаминовой кислоты и лизина.

Полиэлектролиты, за исключением белков, характеризуются высокой плотностью расположения ионогенных групп – обычно на одно звено цепи приходится по одной ионогенной группе. Вследствие этого молекулы полиэлектролитов могут испытывать в растворе значительные электростатические взаимодействия, что приводит к значительной деформации цепей гибких молекул.

Все высокомолекулярные электролиты растворяются в полярных растворителях, т.к. макромолекулы с гомогенными группами взаимодействуют с полярными жидкостями сильнее, чем с неполярными.

Молекулы белков являются амфотерными соединениями, pH белков ниже 7, т.к. они являются более сильной кислотой, чем основанием.

8. Латексы и дисперсии полимеров. Их применение

Натуральные латексы представляют собой млечный сок бразильской гевеи, синтетические латексы получают путем полимеризации в водной среде непредельных углеводородов – бутадиена, хлоропрена и других мономеров.

Латексы содержат макроскопические и ультра микроскопические частицы, приближающиеся по формуле к сферическим, на поверхности которых адсорбированы стабилизатор – соединения типа белков для натурального латекса и мыла али другие ПАВ у синтетических латексов. Вещество дисперсной фазы состоит из каучука, макромолекулы которого представляют собой гибкие углеводородные цепи, не содержащие или содержащие полярные группы.

Коллоидные системы с твердой дисперсионной средой называют твердые золи. Их можно разделить на системы с газовой, жидкой и твердой дисперсной фазой.

Системы с твердой дисперсионной средой и газовой дисперсной фазой часто называют твердыми пенами.

Системы с твердой дисперсионной средой и жидкой дисперсной фазой можно считать твердыми эмульсиями.

Наибольшее значение имеют системы твердой дисперсионной средой и твердой дисперсной фазой. Натуральные и синтетические латексы широко применяются для получения эластичных пленок, для изготовления эластичных пористых материалов, заменителей кожи, для пропитки корда в шинной промышленности и др.

V. Раздел «Представители гетерогенно – дисперсных систем»

1. Суспензии. Способы получения и стабилизации. Особенности суспензий и их применение

Суспензии – системы с твердой дисперсной фазой и жидкой дисперсионной средой, размеры частиц которых превышают коллоидные размеры.

Методы получения суспензий делят на физико-механические и физико-химические.

К физико-механическим относятся дробление и измельчение твердых материалов, и распыление жидких сред, т.е. диспергирование. В ходе осуществления этого метода химический состав материала не меняется. При физико-химических методах получения суспензий изменяется химический состав материала. К таким методам относятся восстановление оксидов и других металлов, электролиз водных растворов и расплавов солей и др.

Суспензии одновременно поглощают и рассеивают свет, при этом в отличие от опалесцирующих золей суспензии проявляют мутность не только при боковом освещении, но и в проходящем свете. Суспензии, так же как и золи, способны проявлять двойное лучепреломление в потоке.

Поскольку частицы суспензий обладают сравнительно большими размерами, суспензии седиментационно неустойчивы, если плотность дисперсной фазы не очень близка к плотности дисперсной среды и вязкость этой среды не очень велика.

Для суспензий характерен ряд процессов, не свойственных коллоидным системам или протекающих у последних иначе, чем у суспензии. К таким процессам относятся седиментация, флотация, фильтрация и кольматация.

К суспензиям при достаточном содержании влаги относятся почвы и грунты, цементные и известковые растворы, применяемые в строительстве. Суспензиями являются взвеси пигментов в органических средах, применяющихся в качестве масляных красок и цветных лаков, взвеси графита и угля, используемые для создания центров кристаллизации с целью предотвращения образования накипи в котлах и т.д.

2. Эмульсии. Способы получения и стабилизации. Прямые и обратные эмульсии, обращение фаз в эмульсиях, эмульгаторы и деэмульгаторы. Применение эмульсии

Эмульсии – это дисперсные системы, образованные двумя взаимно нерастворимыми жидкостями. Их получают как конденсационными, так и диспергационными методами.

Отличительной особенностью не слишком концентрированных эмульсий является сферическая форма частиц.

Существуют лиофобные и лиофольные – критические эмульсии.

Критические эмульсии – это системы, образующиеся из двух ограниченно смешивающихся жидкостей при температурах, близких к критической температуре смешения, когда поверхностное натяжение на границе фаз становится весьма малым и тепловое движение молекул уже достаточно для диспергирования одной жидкости в другой.

Лиофобные эмульсии классифицируют:

- по полярности дисперсной фазы и дисперсной среды и различают:

1 эмульсии неполярной или слабополярной жидкости в полярной – эмульсии первого рода (прямые);

2 эмульсии полярной жидкости в неполярной – эмульсии второго рода (обратные).

- по концентрации дисперсной фазы в системе эмульсии делят на:

1 разбавленные эмульсии – системы жидкость-жидкость, содержащие до 0,1% дисперсной фазы, обладающие характерными свойствами;

2 концентрированные эмульсии – система жидкость-жидкость со сравнительно значительным содержанием дисперсной фазы, вплоть до 74 %.

3 Высококонцентрированные (желатинированные) эмульсии – с содержанием дисперсной фазы выше, чем 74 %. Их можно приготовить с очень большим содержанием дисперсной фазы и соответственно с ничтожным содержанием дисперсной среды.

Эмульсии агрегативно неустойчивы из-за избытка свободной энергии на межфазной поверхности. На агрегативную устойчивость эмульсий сильнее всего влияют природа и содержание в системе эмульгатора. Эффективность эмульгатора характеризуется специальным числом – гидофильно-липофильным балансом. Если число ГЛБ лежит в пределах 3-6, образуется эмульсия обратная. Эмульгаторы с числом ГЛБ 8-13 дают прямую эмульсию.

Часто перед технологом стоит задача не получить эмульсию, а наоборот, предупредить ее возникновение или разрушить (деэмульгировать) уже образовавшуюся систему. Разрушение всех эмульсий можно достичь введением в систему ПАВ, вытесняющего из адсорбционного слоя эмульгатор, но неспособного стабилизовать эмульсию. Эмульсии можно также разрушить центрифугированием, фильтрованием, электрофорезом.

В пищевой промышленности к эмульсиям принадлежат молочные продукты, маргарин, майонез, различные соусы. В фармацевтической промышленности многие лекарства применяются в виде эмульсий.

3. Пены. Способы получения и стабилизации. Применение пен. Пеногашение

Пены свободнодисперсные системы, состоящие из газообразной дисперсной фазы и жидкой дисперсной среды.

Пены получают диспергационными и конденсационными методами. Пена получается при диспергировании газа в жидкость из узкого отверстия – струя газа разрывается и разбивается на пузырьки. Пена образуется и при механическом перемешивании газа с жидкостью, что можно наблюдать при флотации, стирки и др. процессах. Устойчивость пен обеспечивается с помощью стабилизаторов, в качестве которых применяется ПАВ.

Пены применяются при флотации, при стирке, в противопожарном деле.

4. Аэрозоли. Способы получения и стабилизации. Особенности аэрозолей и их применение. Необходимость и способы разрушения аэрозолей

Аэрозоли – дисперсные системы с газообразной дисперсной средой и взвешенными или жидкими частицами. По методам получения они подразделяются на:

· диспергационные, образующиеся при измельчении и распылении веществ;

· конденсационные, получаемые конденсацией из пересыщенных паров и в результате реакций, протекающих в газовой фазе.

По агрегатному состоянию и размерам частиц дисперсной фазы аэрозоли делят на:

· туманы – системы с жидкой дисперсной фазой, размер частиц 10-0,1мкм;

· пыли – системы с твердыми частицами размером больше 10мкм;

· дымы – размер твердых частиц, которых находится в пределах 10-0,001мкм.

В практике «дым» означает аэродисперсную систему, возникающую при сгорании топлива и содержащие твердые частицы сажи и золы и жидкие частицы продуктов перегонки топлива и капли воды, образовавшиеся в результате конденсации водяного пара.

Туманы имеют частицы правильной сферической формы, а пыли и дымы содержат твердые частицы самой разнообразной формы.

Аэрозоли – сравнительно сильно разреженные системы, обладающие малым коэффициентом внутреннего трения дисперсионной среды.

Аэрозоли, обладая при высокой дисперсности достаточной седиментационной устойчивостью, обычно являются весьма агрегативно-неустойчивыми системами, и в них всегда идет процесс коагуляции.

На скорость разрушения систем с газовой дисперсионной средой влияют такие факторы, как: частота столкновения частиц, полидисперсность, анизодиаметрическая форма частиц. Разрушение аэрозолей ускоряется при наличии в них противоположно заряженных частиц. Наоборот, если частицы аэрозолей обладают одинаковым по знаку и достаточно большим по величине зарядом, то наблюдается рассеяние частиц.

Природные аэрозоли – это облака и туманы, определяют выпадение осадков и в значительной степени обуславливают климат того или иного района. Пыльца растений, споры бактерий и плесени, а также легкие семена переносятся в природе в форме аэрозоля.

Литература

1. Пасынский А.Г. Коллоидная химия. М.: Высшая школа - 1968.

2. Кузнецов В.В. Физическая и коллоидная химия. М.: Высшая школа - 1968.

3. Воюцкий С.С. Курс коллоидной химии. – М.: Химия, 1975.

4. Фролов Ю.Г. Курс коллоидной химии. – М.: Химия, 1982.

5. Фридрихсберг Д.А. Курс коллоидной химии. – Л.: Химия, 1974.