
Рефераты по авиации и космонавтике
Рефераты по административному праву
Рефераты по безопасности жизнедеятельности
Рефераты по арбитражному процессу
Рефераты по архитектуре
Рефераты по астрономии
Рефераты по банковскому делу
Рефераты по сексологии
Рефераты по информатике программированию
Рефераты по биологии
Рефераты по экономике
Рефераты по москвоведению
Рефераты по экологии
Краткое содержание произведений
Рефераты по физкультуре и спорту
Топики по английскому языку
Рефераты по математике
Рефераты по музыке
Остальные рефераты
Рефераты по биржевому делу
Рефераты по ботанике и сельскому хозяйству
Рефераты по бухгалтерскому учету и аудиту
Рефераты по валютным отношениям
Рефераты по ветеринарии
Рефераты для военной кафедры
Рефераты по географии
Рефераты по геодезии
Рефераты по геологии
Рефераты по геополитике
Рефераты по государству и праву
Рефераты по гражданскому праву и процессу
Рефераты по кредитованию
Рефераты по естествознанию
Рефераты по истории техники
Рефераты по журналистике
Рефераты по зоологии
Рефераты по инвестициям
Рефераты по информатике
Исторические личности
Рефераты по кибернетике
Рефераты по коммуникации и связи
Рефераты по косметологии
Рефераты по криминалистике
Рефераты по криминологии
Рефераты по науке и технике
Рефераты по кулинарии
Рефераты по культурологии
Дипломная работа: Теория остатков
Дипломная работа: Теория остатков
МИНИСТЕРСТВО ОБРАЗОВАНИЯ РЕСПУБЛИКИ БЕЛАРУСЬ
Учреждение образования
«Гомельский государственный университет
имени Франциска Скорины »
Математический факультет
Кафедра алгебры и геометрии
Допущена к защите
Зав. кафедрой _________ Шеметков Л.А.
«_____» ____________ 2006 г.
ТЕОРИЯ ОСТАТКОВ
ДИПЛОМНАЯ РАБОТА
Исполнитель:
студентка группы М-52 ____________ Клименко Ю.
Научный руководитель:
к.ф-м.н., доцент кафедры
алгебры и геометрии ____________ Подгорная В.
Рецензент:
ст. преподаватель
кафедры высшей
математики ____________ Курносенко Н.
Гомель 2008
Содержание
Введение. 3
1 Алгоритм Евклида. 4
1.1 Определения алгоритма. 4
1.2 Алгоритм Евклида. 5
1.3 Применения алгоритма Евклида. 12
2 Делимость в кольцах. 17
2.1 Область целостности. 17
2.2 Кольцо частных. 19
2.3 Евклидовы кольца. 21
3 Сравнения и арифметика остатков. 27
4 Функция Эйлера. 41
5 Китайская теорема об остатках. 53
Заключение. 62
Список использованных источников. 63
Введение
История арифметики остатков начинается с исследований К.Ф. Гаусса, который впервые стал рассматривать сравнения. В дальнейшем была обнаружена связь теории сравнений с астрономическими задачами (китайская теорема об остатках). В результате многочисленных исследований теория остатков была распространена на кольца произвольной природы. В последнее время обнаружилось приложение этой теории в криптографии. В дипломной работе изложена теория остатков на современном алгебраическом языке.
Дипломная работа состоит из пяти разделов.
В первом разделе изложено понятие остатка, наибольшего общего делителя, алгоритма Евклида, расширенного алгоритма Евклида и применение алгоритма Евклида для решения линейных диофантовых уравнений и разложение чисел в цепные дроби.
Во втором разделе изложен алгебраический подход к делимости в кольцах. Рассмотрена область целостности, кольцо частных и евклидовы кольца.
В третьем разделе изложены теории вычетов по модулю и теория сравнений. Приведено применении теории остатков в криптографии (алгоритм RSA).
В четвертом разделе изложена теория мультипликативных функция и подробно рассмотрена функция Эйлера, с её свойствами.
В пятом разделе изложена китайская теорема об остатках для колец.
1 Алгоритм Евклида
1.1 Определения алгоритма
Единого «истинного» определения понятия «алгоритм» нет.
«Алгоритм — это всякая система вычислений, выполняемых по строго определённым правилам, которая после какого-либо числа шагов заведомо приводит к решению поставленной задачи.» (А. Колмогоров)
«Алгоритм — это точное предписание, определяющее вычислительный процесс, идущий от варьируемых исходных данных к искомому результату.» (А. Марков)
«Алгоритм есть формализованная последовательность действий (событий). Алгоритм может быть записан словами и изображен схематически. Практически любое неслучайное повторяемое действие поддается описанию через алгоритм.»
«Алгоритм — это система операторов, взятых из множества операторов некоторого исполнителя, которая полностью определяет некоторый класс алгоритмических процессов, то есть процессов, которые:
1. дискретны;
2. детерминированы;
3. потенциально конечны;
4. преобразовывают некоторые конструктивные объекты.
Между операторами алгоритма и операциями (элементарными действиями) алгоритмического процесса существует гомоморфное соответствие. Поэтому алгоритм следует также считать моделью алгоритмического процесса». (А. Копаев)
Формальные признаки алгоритмов
Различные определения алгоритма в явной или неявной форме содержат следующий ряд общих требований:
· детерминированность — определённость. В каждый момент времени следующий шаг работы однозначно определяется состоянием системы. Таким образом, алгоритм выдаёт один и тот же результат (ответ) для одних и тех же исходных данных. В современной трактовке у разных реализаций одного и того же алгоритма должен быть изоморфный граф. С другой стороны, существуют вероятностные алгоритмы, в которых следующий шаг работы зависит от текущего состояния системы и генерируемого случайного числа.
· понятность — алгоритм для исполнителя должен включать только те команды, которые ему (исполнителю) доступны, которые входят в его систему команд.
· завершаемость (конечность) — при корректно заданных исходных данных алгоритм должен завершать работу и выдавать результат за конечное число шагов. С другой стороны, вероятностный алгоритм может и никогда не выдать результат, но вероятность этого равна 0.
· массовость — алгоритм должен быть применим к разным наборам исходных данных.
Современное формальное определение алгоритма было дано в 30-50-х гг. XX века в работах Тьюринга, Поста, Чёрча (тезис Чёрча — Тьюринга), Н. Винера, А. А. Маркова.
1.2 Алгоритм Евклида
Определение. Число d Z , делящее одновременно числа а , b , c , ... , k Z , называется общим делителем этих чисел. Наибольшее d с таким свойством называется наибольшим общим делителем. Обозначение: d = ( a , b , c , ..., k ) .
Теорема. Если ( a , b ) = d , то найдутся такие целые числа u и v , что d = au + bv .
Доказательство. Рассмотрим множество P = { au + bv u,v Z }. Очевидно, что P Z , а знатоки алгебры могут проверить, что P – идеал в Z . Очевидно, что a , b , 0 P . Пусть x , y P и y 0 . Тогда остаток от деления x на y принадлежит P . Действительно:
x = yq + r , 0 r < y ,
r = x – yq = ( au 1 + bv 1 ) – ( au 2 + bv 2 ) q = a ( u 1 – u 2 q )+ b ( v 1 – v 2 q ) P .
Пусть d P - наименьшее положительное число из P (призадумайтесь, почему такое имеется!). Тогда а делится на d . В самом деле, a = dq + r 1 , 0 r 1 < d , a P , d P , значит r 1 P , следовательно r 1 = 0. Аналогичными рассуждениями получается, что b делится на d , значит d - общий делитель a и b .
Далее, раз d P , то d = au 0 + bv 0 . Если теперь d 1 - общий делитель a и b , то d 1 | ( au 0 + bv 0 ), т.е. d 1 | d . Значит d d 1 и d - наибольший общий делитель.
Определение. Целые числа a и b называются взаимно простыми, если (a , b ) = 1.
Вспоминая свойство 1 из предыдущего пункта, легко заметить, что два числа a и b являются взаимно простыми тогда и только тогда, когда найдутся целые числа u и v такие, что au + bv = 1.
Пусть даны два числа a и b ; a 0, b 0, считаем, что a > b . Символом := в записи алгоритма обозначаем присваивание. Алгоритм:
1. Ввести a и b .
2. Если b = 0 , то Ответ: а . Конец .
|
a = bq 1 + r 1 b = r 1 q 2 + r 2 r 1 = r 2 q 3 + r 3 r 2 = r 3 q 4 + r 4 |
0 r 1 < b 0 r 2 < r 1 0 r 3 < r 2 0 r 4 < r 3 |
| · · · · · · · · · | |
|
r n -3 = r n -2 q n -1 + r n -1 r n -2 = r n -1 q n + r n r n -1 = r n q n +1 |
0 r n -1 < r n -2 0 r n < r n -1 r n +1 = 0 |
3. Заменить r := "остаток от деления а на b ", а := b , b := r .
4. Идти на 2.
В современной буквенной записи, алгоритм Евклида выглядит так: a > b; a, b Z .
Имеем: b > r 1 > r 2 >... > r n > 0, следовательно процесс оборвется максимум через b шагов. Очень интересный и практически важный народохозяйственный вопрос о том, когда алгоритм Евклида работает особенно долго, а когда справляется с работой молниеносно, мы рассмотрим чуть позже. Давайте сейчас покажем, что r n = ( a , b ). Просмотрим последовательно равенства сверху вниз: всякий делитель а и b делит r 1 , r 2 ,..., r n . Если же просматривать эту цепочку равенств от последнего к первому, то видно, что r n | r n -1 , r n | r n -2 , и т.д., т.е. r n делит а и b . Поэтому r n - наибольший общий делитель чисел а и b .
Как и всякая добротно выполненная работа, алгоритм Евклида дает гораздо больше, чем от него первоначально ожидалось получить. Из его разглядывания ясно, например, что совокупность делителей а и b совпадает с совокупностью делителей ( a , b ). Еще он дает практический способ нахождения чисел u и v из Z (или, если угодно, из теоремы пункта 2) таких, что r n = au + bv = ( a, b ).
Действительно, из цепочки равенств имеем:
r n = r n -2 - r n -1 q n = r n -2 - ( r n -3 - r n -2 q n -1 ) q n = ...
(идем по цепочке равенств снизу вверх, выражая из каждого следующего равенства остаток и подставляя его в получившееся уже к этому моменту выражение)
... = au + bv = ( a , b ).
Пример. Пусть а = 525, b = 231. (ниже приводится запись деления уголком, и каждый раз то, что было в уголке, т.е. делитель, приписывается к остатку от деления с левой стороны, а остаток, как новый делитель, берется в уголок)
|
_ _42| 42 | 0 |
_ 63| 42 | 21 2 |
_ 231| 189 | 42 1 |
525| 462 | 63 3 |
231 2 |
Запись того же самого в виде цепочки равенств:
525 = 231 · 2 + 63
231 = 63 · 3 + 42
63 = 42 · 1 + 21
42 = 21 · 2
Таким образом, (525, 231) = 21. Линейное представление наибольшего общего делителя:
21 = 63 - 42 · 1 = 63 - (231 - 63 · 3) · 1 =
= 525 - 231 · 2 - (231 - (525 - 231 · 2) · 3) =
= 525 · 4 - 231 · 9,
и наши пресловутые u и v из Z равны, соответственно, 4 и - 9.
Приступим теперь к исполнению второй части названия этого пункта - анализу алгоритма Евклида. Нас будет интересовать наихудший случай - когда алгоритм работает особенно долго? Спросим точнее: какие два наименьших числа надо засунуть в алгоритм Евклида, чтобы он работал в точности заданное число шагов? Ответ на этот вопрос дает
Теорема (Ламэ, 1845 г.). Пусть n N , и пусть a > b > 0 такие, что алгоритму Евклида для обработки а и b необходимо выполнить точно n шагов (делений с остатком), причем а - наименьшее с таким свойством. Тогда а = n +2 , b = n +1 , где k - k- ое число Фибоначчи.
Следствие. Если натуральные числа a и b не превосходят N N , то число шагов (операций деления с остатком), необходимых алгоритму Евклида для обработки a и b не превышает log Ф ( 5 N ) - 2, где - верхнее целое , = (1 + 5)/2 - больший корень характеристического уравнения последовательности Фибоначчи.
Доказательство. Максимальное число шагов n достигается при а = n+2 , b = n +1 , где n - наибольший номер такой, что n +2 < N . Рассматривая формулу для n -ого члена последовательности Фибоначчи, легко понять, что n +2 - ближайшее целое к (1/ 5) n +2 . Значит (1/ 5) n +2 < N , следовательно, n+2 < log Ф ( 5 N ), откуда моментально даже n < log Ф ( 5 N ) - 3 (именно "минус три", ведь рассматривается верхнее целое).
log Ф ( 5 N ) 4,785 · lg N + 1,672, поэтому, например, с любой парой чисел, меньших миллиона, алгоритм Евклида разбирается не более, чем за 4,785 · 6 + 1,672 - 3 = 31 - 3 = 28 шагов.
Листинг алгоритма Евклида на языке С
// Обобщенный алгоритм Евклида для поиска наибольшего общего
// делителя gcd = НОД(u,v) целых положительных чисел u и v
// и коэффициентов a и b уравнения a*u + b*v = gcd
// Все числа полагаются типа long
// Подстановки упрощающие запись исходного текста
#define isEven(x) ((x & 0x01L) == 0) // x - четное?
#define isOdd(x) ((x & 0x01L)) // x - нечетное?
#define swap(x,y) (x ^= y, y ^= x, x ^= y) // обмен значений x и y
void GenEuclid(long *u, long *v, long *a, long *b, long *gcd)
{
int k; // Параметр циклов
long a1, b1, g1; // Вспомогательные переменные
// Алгоритм предполагает, что u > v, если u < v, то они переставляются
if (*u < *v) swap(*u, *v);
// Если u = n * 2^k1 или v = m * 2^k2, то перед поиском НОД
// производим сокращение u = u/(2^k), v = v/(2^k),
// где k - минимальное из k1, k2. Показатель k запоминаем.
for (k = 0; isEven(*u) && isEven(*v); ++k){
*u >>= 1; *v >>= 1;
}
// Задание начальных значений
*a = 1; *b = 0; *gcd = *u; a1 = *v; b1 = *u - 1; g1 = *v;
do {
do {
if (isEven(*gcd)){
if (isOdd(*a) || isOdd(*b)){
*a += *v; *b += *u;
}
*a >>= 1; *b >>= 1; *gcd >>= 1;
}
if (isEven(g1) || *gcd < g1){
swap(*a, a1); swap(*b, b1); swap(*gcd, g1);
}
} while (isEven(*gcd));
while(*a < a1 || *b < b1){
*a += *v; *b += *u;
}
*a -= a1; *b -= b1; *gcd -= g1;
} while (g1 > 0);
while (*a >= *v && *b >= *u){
*a -= *v; *b -= *u;
}
// производим умножение коэффициентов уравнения
// на сокращенный ранее множитель 2^k
*a <<= k; *b <<= k; *gcd <<= k;
}
Расширенный алгоритм Евклида и соотношение Безу
Формулы для ri могут быть переписаны следующим образом:
r1 = a + b( - q0)
r2 = b − r1q1 = a( − q1) + b(1 + q1q0)
![]()
(a,b) = rn = as + bt
здесь s и t целые. Это представление наибольшего общего делителя называется соотношением Безу, а числа s и t — коэффициентами Безу. Соотношение Безу является ключевым в доказательстве основной теоремы арифметики.
1.3 Применения алгоритма Евклида
Пусть требуется решить линейное диофантово уравнение:
ax + by = c ,
где a , b , c Z ; a и b - не нули.
Попробуем порассуждать, глядя на это уравнение.
Пусть ( a , b ) = d . Тогда a = a 1 d ; b = b 1 d и уравнение выглядит так:
a 1 d· x + b 1 d· y = c , т.е. d· ( a 1 x + b 1 y ) = c .
Теперь ясно, что у такого уравнения имеется решение (пара целых чисел x и y ) только тогда, когда d | c . Пусть d | c . Поделим обе части уравнения на d , и всюду далее будем считать, что ( a , b ) = 1.
Рассмотрим несколько случаев.
Случай 1. Пусть c = 0, уравнение имеет вид ax + by = 0 - " однородное линейное диофантово уравнение".
| x = - |
b a |
y . |
Так как x должен быть целым числом, то y = at , где t - произвольное целое число (параметр). Значит x = - bt и решениями однородного диофантова уравнения ax + by = 0 являются все пары вида {- bt , at }, где t = 0; ±1; ±2;... Множество всех таких пар называется общим решением линейного однородного диофантова уравнения, любая же конкретная пара из этого множества называется частным решением.
Случай 2. Пусть теперь c 0. Этот случай закрывается следующей теоремой.
Теорема. Пусть ( a , b ) = 1, { x 0 , y 0 } - частное решение диофантова уравнения ax + by = c . Тогда его общее решение задается формулами:
|
|
x = x 0 - bt y = y 0 + at . |
Таким образом, и в теории линейных диофантовых уравнений общее решение неоднородного уравнения есть сумма общего решения соответствующего однородного уравнения и некоторого (любого) частного решения неоднородного уравнения.
Доказательство. То, что правые части указанных в формулировке теоремы равенств действительно являются решениями, проверяется их непосредственной подстановкой в исходное уравнение. Покажем, что любое решение уравнения ax + by = c имеет именно такой вид, какой указан в формулировке теоремы. Пусть { x * , y *} - какое-нибудь решение уравнения ax + by = c . Тогда ax * + by * = c , но ведь и ax 0 + by 0 = c . Следуя многолетней традиции доказательства подобных теорем, вычтем из первого равенства второе и получим:
a ( x *- x 0 ) + b ( y *- y 0 ) = 0
- однородное уравнение. Далее, глядя на случай 1, рассмотрение которого завершилось несколькими строками выше, пишем сразу общее решение: x *- x 0 = - bt , y *- y 0 = at , откуда моментально, используя навыки третьего класса средней школы, получаем:
|
|
x * = x 0- bt , y * = y 0 + at. |
Как же искать то самое частное решение { x 0 , y 0 }. Мы договорились, что ( a , b ) = 1. Это означает, что найдутся такие u и v из Z , что au + bv = 1, причем эти u и v мы легко умеем находить с помощью алгоритма Евклида. Умножим теперь равенство au + bv = 1 на c и получим: a ( uc ) + b ( vc ) = c , т.е. x 0 = uc , y 0 = vc .
Определение. Цепной (или, непрерывной) дробью называется выражение вида:
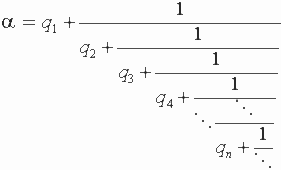
(Бедные наборщики в докомпьютерные времена буквально стрелялись, когда им приходилось набирать в книжках подобные многоэтажные выражения.) Договоримся называть числа q 1 , q 2 ,..., q n ,... - неполными частными и считаем, что q 1 Z , а q 2 ,..., q n ,... N . Числа называются подходящими дробями цепной дроби .
| 1 = q 1 , 2 , = q 1 + |
1 q 2 |
, 3 = q 1 + |
1
|
, и т. д. |
Цепная дробь может быть как конечной (содержащей конечное число дробных линий и неполных частных), так и бесконечной вниз и вправо (на юго-восток). В первом случае она, очевидно, представляет некоторое рациональное число, во втором случае - пока непонятно что она вообще из себя представляет, но ясно, что все ее подходящие дроби - рациональные числа.
Пусть Q , = a / b ; a , b Z , b > 0. Оказывается, что при этих условиях, указанный выше процесс разложения числа в цепную дробь всегда конечен и выполним с помощью достопочтенного и любимого нами алгоритма Евклида. Действительно, отдадим алгоритму числа a и b , и внимательно посмотрим, что получится.
a = bq 1 + r 1 |
т.е. |
a b |
= q 1 + |
1 b / r 1 |
| b = r 1 q 2 + r 2 | т.е. |
b r 1 |
= q 2 + |
1 r 1 / r 2 |
| r 1 = r 2 q 3 + r 3 | т.е. |
r 1 r 2 |
= q 3 + |
1 r 2 / r 3 |
| . . . . . . . | ||||
| r n -2 = r n -1 q n + r n | т.е. |
r n -2 r n -1 |
= q n + |
1 r n -1 / r n |
| r n -1 = r n q n +1 | т.е. |
r n -1 r n |
= q n +1 . | |
Значит:
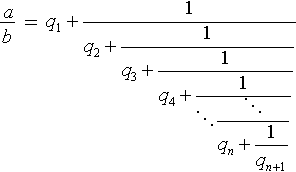
где q 1 , q 2 ,..., q n +1 - как раз те самые неполные частные из алгоритма Евклида (вот откуда название этих чисел в цепных дробях). Таким образом, в случае рационального числа a / b , процесс разложения в цепную дробь конечен и дробь содержит не более b этажей. Наиболее одаренные читатели в этом месте уже поняли, что основная теорема о цепных дробях для рациональных чисел оказалась почти доказана (не доказали только единственность разложения, но она в случае конечных цепных дробей почти очевидна - приравняйте две цепных дроби и, рассуждая по индукции, получите, что у равных дробей совпадают все неполные частные).
Пример. Пример заимствован из книги И. М. Виноградова "Основы теории чисел". Итак: разложить 105/38 в цепную дробь.
Включаем алгоритм Евклида:
105 = 38 · 2 + 29
38 = 29 · 1 + 9
29 = 9 · 3 + 2
9 = 2 · 4 + 1
2 = 1 · 2
Неполные частные я специально подчеркнул потому, что теперь для написания ответа нужно аккуратно расположить их подряд на этажах цепной дроби перед знаками плюс:
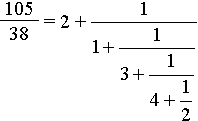
2 Делимость в кольцах
2.1 Область целостности
Область целостности (или целостное кольцо, или область цельности) — понятие абстрактной алгебры: ассоциативное коммутативное кольцо с единицей, в котором 0≠1 и произведение двух ненулевых элементов не равно нулю. Условие 0≠1 исключает из рассмотрения тривиальное кольцо {0}.
Эквивалентное определение: область целостности — это ассоциативное коммутативное кольцо, в котором нулевой идеал {0} является простым. Любая область целостности является подкольцом своего поля частных.
·
Простейший пример
области целостности — кольцо целых чисел ![]() .
.
· Любое поле является областью целостности. С другой стороны, любая артинова область целостности есть поле. В частности, все конечные области целостности суть конечные поля.
·
Кольцо
многочленов с коэффициентами из некоторого целостного кольца также является
целостным. Например, целостными будут кольцо ![]() многочленов
одной переменной с целочисленными коэффициентами и кольцо
многочленов
одной переменной с целочисленными коэффициентами и кольцо ![]() многочленов
двух переменных с вещественными коэффициентами.
многочленов
двух переменных с вещественными коэффициентами.
·
Множество действительных
чисел вида ![]() есть подкольцо поля
есть подкольцо поля ![]() , а значит, и
область целостности. То же самое можно сказать про множество комплексных чисел
вида a + bi, где a
и b целые (множество Гауссовых целых).
, а значит, и
область целостности. То же самое можно сказать про множество комплексных чисел
вида a + bi, где a
и b целые (множество Гауссовых целых).
·
Пусть U — связное открытое подмножество комплексной
плоскости ![]() . Тогда кольцо H(U)
всех голоморфных функций
. Тогда кольцо H(U)
всех голоморфных функций ![]() будет целостным. То же самое верно
для любого кольца аналитических функций, определённых на связном подмножестве
аналитического многообразия.
будет целостным. То же самое верно
для любого кольца аналитических функций, определённых на связном подмножестве
аналитического многообразия.
· Если K — коммутативное кольцо, а I — идеал в K, то факторкольцо K / I целостное тогда и только тогда, когда I — простой идеал.
Делимость, простые и неприводимые элементы
Пусть a и b — элементы
целостного кольца K. Говорят, что «a делит b» или «a — делитель b»
(и пишут ![]() ), если и только если существует элемент
), если и только если существует элемент ![]() такой, что ax = b.
такой, что ax = b.
Делимость транзитивна: если a делит b и b делит c, то a делит c. Если a делит b и c, то a делит также их сумму b + c и разность b - c.
Для кольца K с единицей элементы ![]() , которые делят 1,
называются делителями единицы, а иногда и просто единицами. Они и
только они, обратимы в K. Единицы делят все
остальные элементы кольца.
, которые делят 1,
называются делителями единицы, а иногда и просто единицами. Они и
только они, обратимы в K. Единицы делят все
остальные элементы кольца.
Элементы a и b называются ассоциированными, если a делит b и b делит a. a и b ассоциированны тогда и только тогда, когда a = b * e, где e — обратимый элемент.
Необратимый элемент q целостного кольца называется неприводимым, если его нельзя разложить в произведение двух необратимых элементов.
Ненулевой
необратимый элемент p называется простым,
если из того, что ![]() , следует
, следует ![]() или
или
![]() . Это определение обобщает понятие простого числа в кольце
. Это определение обобщает понятие простого числа в кольце ![]() ,
однако учитывает и отрицательные простые числа. Если p
— простой элемент кольца, то порождаемый им главный идеал (p)
будет простым. Любой простой элемент неприводим, но обратное верно не во всех
областях целостности.
,
однако учитывает и отрицательные простые числа. Если p
— простой элемент кольца, то порождаемый им главный идеал (p)
будет простым. Любой простой элемент неприводим, но обратное верно не во всех
областях целостности.
· Любое поле, а также любое кольцо с единицей, содержащееся в некотором поле, является областью целостности.
Обратно, любая область целостности может быть вложена в некоторое поле. Такое вложение дает конструкция поля частных.
· Если A ― область целостности, то кольцо многочленов и кольцо формальных степенных рядов над A также будут областями целостности.
· Если A ― коммутативное кольцо с единицей и I ― некоторый идеал в A, то кольцо A / I является областью целостности тогда и только тогда, когда идеал I прост.
· Кольцо будет областью целостности тогда и только тогда, когда его спектр есть неприводимое топологическое пространство.
· Прямое произведение колец никогда не бывает областью целостности, так как единица первого кольца, умноженная на единицу второго кольца, даст 0.
· Тензорное произведение целостных колец тоже будет целостным кольцом.
Иногда в определении области целостности не требуют коммутативности. Примерами некоммутативных областей целостности являются тела, а также подкольца тел, содержащие единицу, например целые кватернионы. Однако, вообще говоря, неверно, что любая некоммутативная область целостности может быть вложена в некоторое тело.
2.2 Кольцо частных
В
коммутативной алгебре кольцом частных S-1R кольца R
(коммутативного с единицей) по мультипликативной системе ![]() называется
пространство дробей с числителями из R и знаменателями из S с
арифметическими операциями и отождествлениями, обычными для дробей.
называется
пространство дробей с числителями из R и знаменателями из S с
арифметическими операциями и отождествлениями, обычными для дробей.
Мультипликативной
системой в кольце R
называется подмножество S в R, содержащее 1, не содержащее нуля и
замкнутое по умножению (в кольце R). Для мультипликативной системы S
множество ![]() образует идеал в кольце R.
В случае, когда множество S не содержит делителей нуля кольца R,
идеал IS = (0) и система S
называется регулярной. Если R - целостное кольцо, в ней всякая
мультипликативная система регулярна.
образует идеал в кольце R.
В случае, когда множество S не содержит делителей нуля кольца R,
идеал IS = (0) и система S
называется регулярной. Если R - целостное кольцо, в ней всякая
мультипликативная система регулярна.
Элементами кольца
частных кольца R по мультипликативной системе S являются
формальные дроби вида r/s, где r - произвольный элемент R,
а s - элемент множества S. Две дроби r1
/ s1 и r2 / s2
считаются эквивалентными (представляют один и тот же элемент кольца частных),
если ![]() . Операции сложения и умножения определяются как
обычно:
. Операции сложения и умножения определяются как
обычно:
![]()
![]()
Проверяется, что если в сумме или произведении дроби заменить на эвивалентные, новый результат будет выражаться дробью, эквивалентной прежней. С такими операциями множество S − 1R приобретает структуру коммутативного кольца с единицей. Нулём в нём служит дробь 0/1, единицей - дробь 1/1.
Свойства
· Кольцо частных имеет каноническую структуру алгебры над кольцом R, так как вместе с кольцом S-1R сразу определён и канонический гомоморфизм кольца R в S-1R (каждому элементу r из R соответствует дробь r/1). Ядром этого гомоморфизма является идеал IS. В случае, если система S регулярна (не содержит делителей нуля), этот гомоморфизм инъективен, и кольцо R, таким образом, вложено в своё кольцо частных по системе S. При этом дробь r/s является единственным решением уравнения sx = r.
· Если оба элемента r и s принадлежат S, тогда в кольце S-1R содержатся дроби r/s и s/r. Их произведение равно 1, следовательно, они обратимы. Обратно: каждый обратимый элемент кольца S-1R имеет вид er/s, где r и s принадлежат S, а e - обратимый элемент кольца R.
· Если кольцо R не имеет (собственных) делителей нуля (т.е. это целостное кольцо), множество всех ненулевых элементов образует мультипликативную систему S. Соответствующее кольцо частных будет полем, которое называется полем частных целостного кольца. Отсюда следует, что каждое целостное кольцо вложено в некоторое поле, а именно - в своё поле частных.
· Если R - евклидово кольцо, то всякое кольцо, промежуточное между R и его полем частных, является кольцом частных кольца R по некоторой мультипликативной системе S.
· Если система S состоит из одних только обратимых элементов кольца R, канонический гомоморфизм кольца R в S-1R превращается в изоморфизм, так как каждая дробь r/s оказывается сократимой в кольце R.
· Если кольцо R' является подкольцом кольца R, то множество всех элементов из R', обратимых в кольце R, образует регулярную мультипликативную систему S в кольце R'. Тогда каждой дроби r/s однозначно соответствует некоторый элемент кольца R. Множество всех таких элементов кольца R образует кольцо частных кольца R' в кольце R.
Примеры
·
Полем частных
кольца целых чисел ![]() является поле
рациональных чисел
является поле
рациональных чисел ![]() .
.
·
Степени числа 10
в ![]() образуют мультипликативную систему. Кольцом частных по ней
будет кольцо конечных десятичных дробей.
образуют мультипликативную систему. Кольцом частных по ней
будет кольцо конечных десятичных дробей.
· Полем частных кольца многочленов k[X1,X2,...,Xn] над полем k будет поле рациональных функций k(X1,X2,...,Xn).
·
Пусть ![]() — простой идеал в R. Тогда
дополнение к нему - мультипликативная система. Кольцо частных по ней называется
локализацией кольца R
по простому идеалу
— простой идеал в R. Тогда
дополнение к нему - мультипликативная система. Кольцо частных по ней называется
локализацией кольца R
по простому идеалу ![]() .
.
·
Чётные числа в ![]() образуют
простой идеал. Локализацией кольца
образуют
простой идеал. Локализацией кольца ![]() по нему будет
кольцо рациональных дробей, у которых в несократимом виде знаменатель —
нечётное число.
по нему будет
кольцо рациональных дробей, у которых в несократимом виде знаменатель —
нечётное число.
2.3 Евклидовы кольца
Неформально, евклидово кольцо — в абстрактной алгебре — кольцо, в котором «работает» алгоритм Евклида.
Евклидово
кольцо — это область
целостности R, для которой определена евклидова функция (евклидова
норма) ![]() ,
причём
,
причём ![]() , и возможно деление с остатком, по
норме меньшим делителя, то есть для любых
, и возможно деление с остатком, по
норме меньшим делителя, то есть для любых ![]() имеется
представление a = bq + r, для
которого d(r) < d(b).
имеется
представление a = bq + r, для
которого d(r) < d(b).
Часто на
евклидову норму накладывают дополнительное ограничение: ![]() для
любых a и ненулевых b из кольца R. Если на R задана
норма, не удовлетворяющая этому условию, её можно поправить, переопределив:
для
любых a и ненулевых b из кольца R. Если на R задана
норма, не удовлетворяющая этому условию, её можно поправить, переопределив:
![]()
Такая норма
нужному неравенству удовлетворяет, однако прежний алгоритм деления с остатком
уже не годится — его тоже надо поправлять. Пусть ![]() таков, что d'(b) = d(bx). Разделим с
остатком ax на bx: ax = bxq' + r'x,
где r' = a − bq' и d(r'x) < d(bx) = d'(b).
Так как из определения
таков, что d'(b) = d(bx). Разделим с
остатком ax на bx: ax = bxq' + r'x,
где r' = a − bq' и d(r'x) < d(bx) = d'(b).
Так как из определения ![]() , мы
получили представление a = bq' + r'
с d'(r') < d'(b), что
и требовалось.
, мы
получили представление a = bq' + r'
с d'(r') < d'(b), что
и требовалось.
Тем не менее бонусов от такой нормы не так много — все обратимые элементы имеют одно и то же значение нормы, причём минимальное из всех (конечных), собственные делители элемента a имеют меньшее значение нормы, а также упрощается непосредственное доказательство факториальности евклидовых колец (без ссылки на факториальность колец главных идеалов, доказательство чего требует применения трансфинитной индукции). Основные же свойства евклидовых колец остаются в силе и без этого дополнительного свойства.
·
Кольцо целых
чисел Z. Пример евклидовой функции — абсолютное значение ![]() .
.
· Кольцо целых гауссовых чисел Z[i] (где i — мнимая единица, i2 = − 1) с нормой d(a + ib) = a2 + b2 — евклидово.
· Произвольное поле K является евклидовым кольцом с нормой, равной 1 для всех элементов, кроме 0.
· Кольцо многочленов в одной переменной K[x] над полем K. Пример евклидовой функции — степень deg.
· Кольцо формальных степенных рядов K[[x]] над полем K является евклидовым кольцом. Норма степенного ряда — номер первого ненулевого коэффициента в нём (для нулевого ряда норма равна минус бесконечности).
· Обобщая предыдущий пример, всякое локальное кольцо является евклидовым, если в нём максимальный идеал является главным и пересечение всех его степеней состоит только из нуля. Норма обратимого элемента — 0, необратимого ненулевого — равна максимальной степени максимального идеала, которая содержит данный элемент, а норма нуля — минус бесконечность.
· Кольцо функций H(K), голоморфных на связном компакте K в C (каждая из них должна быть голоморфна в какой-нибудь окрестности этого компакта; две такие функции считаются равными в H(K), если они совпадают в некоторой окрестности K), тоже евклидово. За норму ненулевой функции принимается число нулей (с учётом кратности), которые она принимает на K.
· Счётное пересечение евклидовых колец (подколец в каком-нибудь кольце) не обязано быть евклидовым кольцом (и даже нётеровым или факториальным). Например, кольцо функций H(D), голоморфных в открытом круге D, является пересечением евклидовых колец функций H(K), голоморфных на замкнутых кругах K, содержащихся внутри D (см. предыдущий пример), однако оно ни нётерово, ни факториально, соответственно, и неевклидово.
· Кольцо частных S-1R евклидова кольца R по мультипликативной системе S тоже является евклидовым. Нормой дроби x из S-1R принимается
![]() , где dR — евклидова норма в R, а dS — норма в S-1R.
, где dR — евклидова норма в R, а dS — норма в S-1R.
Деление с остатком определяется так. Пусть есть две ненулевые дроби x = r / t и y из S-1R. По определению нормы в S-1R существует элементы u в R и s в S, такие что y = u / s и dS(y) = dR(u). Произведём деление с остатком в кольце R элементов rs и u:
rs = uq + r', так что dR(r')
< dR(u). Тогда r
/ t = (u / s)(q / t) + r' / ts.
Из построения следуют неравенства ![]() .
.
· Евклидовыми являются кольца конечных двоичных и конечных десятичных дробей, так как они являются кольцами частных кольца целых чисел Z.
· Евклидовыми являются кольца рациональных функций над полем C с фиксированными полюсами, так как такие кольца являются кольцами частных кольца многочленов C[x].
В евклидовом
кольце осуществим алгоритм Евклида нахождения наибольшего общего делителя двух
чисел (элементов). Пусть изначально даны два элемента a0 и a1,
причём ![]() и
и ![]() . Деление с
остатком даёт элемент a2 = a0
− a1q1 с d(a2)
< d(a1). Если он не равен нулю, можно опять
применить деление с остатком, и получить элемент a3
= a1 − a2q2,
и т. д. Таким образом генерируется цепочка значений
. Деление с
остатком даёт элемент a2 = a0
− a1q1 с d(a2)
< d(a1). Если он не равен нулю, можно опять
применить деление с остатком, и получить элемент a3
= a1 − a2q2,
и т. д. Таким образом генерируется цепочка значений ![]() с
с ![]() . Однако эта цепочка прерывается,
поскольку всякое число из
. Однако эта цепочка прерывается,
поскольку всякое число из ![]() может
строго превосходить лишь конечное количество других таких чисел. Это означает,
что при некотором n остаток an+1 равен нулю, а an
не равен, он и есть НОД элементов a0 и a1.
Следовательно, в евклидовом кольце гарантировано завершение алгоритма Евклида.
Строго говоря, именно в евклидовых кольцах и возможна реализация алгоритма
Евклида.
может
строго превосходить лишь конечное количество других таких чисел. Это означает,
что при некотором n остаток an+1 равен нулю, а an
не равен, он и есть НОД элементов a0 и a1.
Следовательно, в евклидовом кольце гарантировано завершение алгоритма Евклида.
Строго говоря, именно в евклидовых кольцах и возможна реализация алгоритма
Евклида.
· В евклидовом кольце каждый идеал — главный (в частности, все евклидовы кольца нётеровы).
o Пусть I — произвольный идеал в евклидовом кольце. Если он содержит лишь 0, — он главный. В противном случае среди его ненулевых элементов найдётся элемент f с минимальной нормой (принцип минимума для натуральных чисел). Он делит все остальные элементы идеала: Если g — произвольный элемент идеала I, представим его в виде g = fq + r с d(r)<d(f). Тогда r - тоже элемент идеала I и он обязан быть нулём, так как его норма меньше, чем у f. Следовательно, идеал I содержится в идеале (f). С другой стороны, всякий идеал, содержащий элемент f, содержит идеал (f). Значит, I = (f) - главный идеал.
· Каждое евклидово кольцо факториально, то есть каждый элемент представим конечным произведением простых элементов, и притом однозначно (с точностью до их перестановки и умножения на обратимые элементы). Факториальность - общее свойство всех колец главных идеалов.
·
Каждое евклидово
кольцо R целозамкнуто, то есть если дробь ![]() , является
корнем многочлена
, является
корнем многочлена ![]() со старшим
коэффициентом, равным 1, тогда a делится на b. Целозамкнутость - общее свойство всех
факториальных колец.
со старшим
коэффициентом, равным 1, тогда a делится на b. Целозамкнутость - общее свойство всех
факториальных колец.
Свойства модулей над евклидовым кольцом
Пусть R - евклидово кольцо. Тогда конечнопорождённые R-модули обладают следующими свойствами:
· Всякий подмодуль N конечнопорождённого R-модуля M конечно порождён. (следствие нётеровости кольца R)
· Ранг подмодуля N не превосходит ранга модуля M. (следствие главности идеалов в R)
· Подмодуль свободного R-модуля свободен. (то же)
·
Гомоморфизм ![]() конечнопорождённых
R-модулей всегда приводится к нормальной форме. То есть существуют
образующие (базис, если модуль свободен)
конечнопорождённых
R-модулей всегда приводится к нормальной форме. То есть существуют
образующие (базис, если модуль свободен) ![]() модуля N,
образующие (базис)
модуля N,
образующие (базис) ![]() модуля M,
номер
модуля M,
номер ![]() и
и ![]() - элементы
кольца R, такие что ai
делит ai + 1 и при i>k
Aui = 0, а при остальных — Aui = aivi.
При этом коэффициенты
- элементы
кольца R, такие что ai
делит ai + 1 и при i>k
Aui = 0, а при остальных — Aui = aivi.
При этом коэффициенты ![]() определены
однозначно с точностью до умножения на обратимые элементы кольца R. (Тут
прямо задействована евклидовость кольца R.)
определены
однозначно с точностью до умножения на обратимые элементы кольца R. (Тут
прямо задействована евклидовость кольца R.)
3 Сравнения и арифметика остатков
Определение. Пусть а, b Z , m N . Говорят, что число а сравнимо с b по модулю m , если а и b при делении на m дают одинаковые остатки. Запись этого факта выглядит так:
a b(mod m) .
Очевидно, что бинарное отношение сравнимости m (неважно, по какому модулю) есть отношение эквивалентности на множестве целых чисел, а любители алгебры скажут, что это отношение является даже конгруэнцией кольца Z , фактор-кольцо по которой Z/ m называется кольцом вычетов и обозначается Z m .
Ясно, что число a сравнимо с b по модулю m тогда и только тогда, когда a-b делится на m нацело. Очевидно, это, в свою очередь, бывает тогда и только тогда, когда найдется такое целое число t , что a=b+mt . Знатоки алгебры добавят к этим эквивалентным утверждениям, что сравнимость a с b по модулю m означает, что a и b представляют один и тот же элемент в кольце Z m .
Свойство 1. Сравнения по одинаковому модулю можно почленно складывать.
Доказательство. Пусть a1b1(mod m), a2b2(mod m). Это означает, что a 1 =b 1 +mt 1 , a 2 =b 2 +mt 2 . После сложения последних двух равенств получим a 1 +a 2 =b 1 +b 2 +m(t 1 +t 2 ) , что означает a 1 +a 2 b 1 +b 2 (mod m).
Свойство 2. Слагаемое, стоящее в какой-либо части сравнения, можно переносить в другую часть, изменив его знак на обратный.
Доказательство.
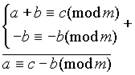
Свойство 3. К любой части сравнения можно прибавить любое число, кратное модулю.
Доказательство.
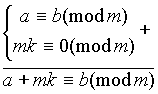
Свойство 4. Сравнения по одинаковому модулю можно почленно перемножать и, следовательно,
Свойство 5. Обе части сравнения можно возвести в одну и ту же степень.
Доказательство.
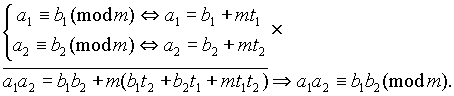
Как следствие из вышеперечисленных свойств, получаем
Свойство 6. Если
a 0 b 0 (mod m) , a 1 b 1 (mod m) ,..., a n b n (mod m) , x y(mod m) ,
то a 0 x n +a 1 x n-1 +...+a n b 0 y n +b 1 y n-1 +...+b n (mod m)
Свойство 7. Обе части сравнения можно разделить на их общий делитель, взаимно простой с модулем.
Доказательство. Пусть a b(mod m) , a=a 1 d , b=b 1 d . Тогда (a 1 -b 1 ) d делится на m . Поскольку d и m взаимно просты, то на m делится именно (a 1 -b 1 ) , что означает a 1 b 1 (mod m) .
Свойство 8. Обе части сравнения и его модуль можно умножить на одно и то же целое число или разделить на их общий делитель.
Доказательство.
a b(mod m) a=b+mt ak=bk+mkt ak bk(mod mk) .
Свойство 9. Если сравнение a b имеет место по нескольким разным модулям, то оно имеет место и по модулю, равному наименьшему общему кратному этих модулей.
Доказательство. Если a b(mod m 1 ) и a b(mod m 2 ) , то a-b делится на m 1 и на m 2 , значит a-b делится на наименьшее общее кратное m 1 и m 2 .
Свойство 10. Если сравнение имеет место по модулю m , то оно имеет место и по модулю d , равному любому делителю числа m .
Доказательство очевидно следует из транзитивности отношения делимости: если a b(mod m) , то a-b делится на m , значит a-b делится на d , где d|m .
Свойство 11. Если одна часть сравнения и модуль делятся на некоторое число, то и другая часть сравнения должна делиться на то же число.
Доказательство.
a b(mod m) a=b+mt .
Отношение m сравнимости по произвольному модулю m есть отношение эквивалентности на множестве целых чисел. Это отношение эквивалентности индуцирует разбиение множества целых чисел на классы эквивалентных между собой элементов, т.е. в один класс объединяются числа, дающие при делении на m одинаковые остатки. Число классов эквивалентности m (знатоки скажут - "индекс эквивалентности m ") в точности равно m .
Определение. Любое число из класса эквивалентности m будем называть вычетом по модулю m . Совокупность вычетов, взятых по одному из каждого класса эквивалентности m , называется полной системой вычетов по модулю m (в полной системе вычетов, таким образом, всего m штук чисел). Непосредственно сами остатки при делении на m называются наименьшими неотрицательными вычетами и, конечно, образуют полную систему вычетов по модулю m . Вычет называется абсолютно наименьшим, если наименьший среди модулей вычетов данного класса.
Пример : Пусть m = 5 . Тогда:
0, 1, 2, 3, 4 - наименьшие неотрицательные вычеты;
-2, -1, 0, 1, 2 - абсолютно наименьшие вычеты.
Обе приведенные совокупности чисел образуют полные системы вычетов по модулю 5 .
Лемма 1. 1) Любые m штук попарно не сравнимых по модулю m чисел образуют полную систему вычетов по модулю m .
2) Если а и m взаимно просты, а x пробегает полную систему вычетов по модулю m , то значения линейной формы аx+b , где b - любое целое число, тоже пробегают полную систему вычетов по модулю m .
Доказательство. Утверждение 1) – очевидно. Докажем утверждение 2). Чисел аx+b ровно m штук. Покажем, что они между собой не сравнимы по модулю m . Ну пусть для некоторых различных x 1 и x 2 из полной системы вычетов оказалось, что ax 1 +b ax 2 +b(mod m) . Тогда, по свойствам сравнений из предыдущего пункта, получаем:
ax 1 ax 2 (mod m)
x 1 x 2 (mod m)
– противоречие с тем, что x 1 и x 2 различны и взяты из полной системы вычетов.
Поскольку все числа из данного класса эквивалентности получаются из одного числа данного класса прибавлением числа, кратного m , то все числа из данного класса имеют с модулем m один и тот же наибольший общий делитель. По некоторым соображениям, повышенный интерес представляют те вычеты, которые имеют с модулем m наибольший общий делитель, равный единице, т.е. вычеты, которые взаимно просты с модулем.
Определение. Приведенной системой вычетов по модулю m называется совокупность всех вычетов из полной системы, взаимно простых с модулем m .
Приведенную систему обычно выбирают из наименьших неотрицательных вычетов. Ясно, что приведенная система вычетов по модулю m содержит ( m ) штук вычетов, где ( m )– функция Эйлера – число чисел, меньших m и взаимно простых с m . Если к этому моменту вы уже забыли функцию Эйлера, загляните в пункт 14 и убедитесь, что про нее там кое-что говорилось.
Пример. Пусть m = 42. Тогда приведенная система вычетов суть:
1, 5, 11, 13, 17, 19, 23, 25, 29, 31, 37, 41.
Лемма 2. 1) Любые ( m ) чисел, попарно не сравнимые по модулю m и взаимно простые с модулем, образуют приведенную систему вычетов по модулю m .
2) Если ( a,m ) = 1 и x пробегает приведенную систему вычетов по модулю m , то аx так же пробегает приведенную систему вычетов по модулю m .
Доказательство. Утверждение 1) – очевидно. Докажем утверждение 2). Числа аx попарно несравнимы (это доказывается так же, как в лемме 1 этого пункта), их ровно ( m ) штук. Ясно также, что все они взаимно просты с модулем, ибо (a,m)=1, (x,m)=1 (ax.m)=1 . Значит, числа аx образуют приведенную систему вычетов.
Лемма 3. Пусть m 1 , m 2 , ..., m k – попарно взаимно просты и m 1 m 2 ...m k =M 1 m 1 =M 2 m 2 =...=M k m k , где M j =m 1 ...m j-1 m j+1 ...m k
1) Если x 1 , x 2 , ..., x k пробегают полные системы вычетов по модулям m 1 , m 2 , ..., m k соответственно, то значения линейной формы M 1 x 1 +M 2 x 2 + ...+M k x k пробегают полную систему вычетов по модулю m=m 1 m 2 ...m k .
2) Если 1 , 2 , ..., k пробегают приведенные системы вычетов по модулям m 1 , m 2 , ..., m k соответственно, то значения линейной формы M 1 1 +M 2 2 + ...+M k k пробегают приведенную систему вычетов по модулю m=m 1 m 2 ...m k .
Доказательство.
1) Форма M 1 x 1 +M 2 x 2 + ...+M k x k принимает, очевидно, m 1 m 2 ...m k =m значений. Покажем, что эти значения попарно несравнимы. Ну пусть
M 1 x 1 +M 2 x 2 + ...+M k x k M 1 x 1 +M 2 x 2 + ...+M k x k (mod m)
Всякое M j , отличное от M s , кратно m s . Убирая слева и справа в последнем сравнении слагаемые, кратные m s , получим:
M s x s M s x s (mod m s ) x s x s (mod m s )
– противоречие с тем, что x s пробегает полную систему вычетов по модулю m s .
2). Форма M 1 1 +M 2 2 + ...+M k k принимает, очевидно, ( m 1 ) ( m 2 ) ... ( m k ) = ( m 1 m 2 ... m k )= ( m ) (функция Эйлера мультипликативна!) различных значений, которые между собой по модулю m=m 1 m 2 ...m k попарно несравнимы. Последнее легко доказывается рассуждениями, аналогичными рассуждениям, проведенным при доказательстве утверждения 1) этой леммы. Так как ( M 1 1 +M 2 2 + ...+M k k ,m s )=(M s s ,m s )=1 для каждого 1 s k , то ( M 1 1 +M 2 2 + ...+M k k ,m s )=1 , следовательно множество значений формы M 1 1 +M 2 2 + ...+M k k образует приведенную систему вычетов по модулю m .
Лемма 4. Пусть x 1 , x 2 , ..., x k ,x пробегают полные, а 1 , 2 ,..., k , – пробегают приведенные системы вычетов по модулям m 1 , m 2 , ..., m k и m=m 1 m 2 ...m k соответственно, где (m i m j )=1 при i j . Тогда дроби {x 1 /m 1 +x 2 /m 2 +...+x k /m k } совпадают с дробями {x/m} , а дроби { 1 /m 1 + 2 /m 2 +...+ k /m k } совпадают с дробями { /m} .
Доказательство. Доказательство обоих утверждений леммы 4 легко получается применением предыдущей леммы 3 после того, как вы приведете каждую сумму {x 1 /m 1 +x 2 /m 2 +...+x k /m k } и { 1 /m 1 + 2 /m 2 +...+ k /m k } к общему знаменателю:
{x 1 /m 1 +x 2 /m 2 +...+x k /m k }={(M 1 x 1 +M 2 x 2 +...+M k x k )/m} ;
{ 1 /m 1 + 2 /m 2 +...+ k /m k }={(M 1 1 +M 2 2 +...+M k k )/m} ,
где M j =m 1 ...m j-1 m j+1 ...m k .
Если теперь принять во внимание, что дробные части чисел, получающихся при делении на модуль m любых двух чисел, сравнимых по модулю m , одинаковы (они равны r/m , где r – наименьший неотрицательный вычет из данного класса), то утверждения настоящей леммы становятся очевидными.
Теорема (Эйлер). Пусть m>1 , (a,m)=1 , ( m ) – функция Эйлера. Тогда:
a ( m ) 1(mod m) .
Доказательство. Пусть х пробегает приведенную систему вычетов по mod m :
x=r 1 ,r 2 ,...,r c
где c= (m) их число, r 1 ,r 2 ,..., r c - наименьшие неотрицательные вычеты по mod m . Следовательно, наименьшие неотрицательные вычеты, соответствующие числам ax суть соответственно:
1 , 2 ,..., c
– тоже пробегают приведенную систему вычетов, но в другом порядке (см. Лемму 2 из пункта 17). Значит:
a r 1 (mod m)
a r 2 (mod m)
...
a r c (mod m)
Перемножим эти с штук сравнений. Получится:
a c r 1 r 2 ...r c j 1 j 2 ... j c (mod m)
Так как r 1 r 2 ...r c = 1 2 ... c 0 и взаимно просто с модулем m , то, поделив последнее сравнение на r 1 r 2 ...r c , получим a ( m ) 1(mod m) .
Вторая теорема этого пункта – теорема Ферма – является непосредственным следствием теоремы Эйлера (конечно, при схеме изложения материала, принятой в этой книжке).
Теорема (Ферма). Пусть р – простое число, р не делит a . Тогда:
a p-1 1(mod p) .
Доказательство 1. Положим в условии теоремы Эйлера m=p , тогда (m)=p-1 (см. пункт 14 ) . Получаем a p-1 1(mod p) .
Необходимо отметить важность условия взаимной простоты модуля и числа a в формулировках теорем Эйлера и Ферма. Простой пример: сравнение 6 2 1(mod 3) очевидно не выполняется. Однако можно легко подправить формулировку теоремы Ферма, чтобы снять ограничение взаимной простоты.
Следствие 1. Без всяких ограничений на a Z ,
a p a(mod p) .
Доказательство. Умножим обе части сравнения a p-1 1(mod p) на a . Ясно, что получится сравнение, справедливое и при a , кратном р .
Доказательство 2. Так как р - простое число, то все биномиальные коэффициенты:
(кроме C 0 p и C p p ) делятся на р , ибо числитель выписанного выражения содержит р , а знаменатель не содержит этого множителя. Если вспомнить бином Ньютона, то становится понятно, что разность (A+B) p -A p -B p =C p 1 A p-1 B 1 +C p 2 A p-2 B 2 +...+C p p-2 A 2 B p-2 +C p p-1 A 1 B p-1 , где А и В – какие угодно целые числа, всегда делится на р . Последовательным применением этого незатейливого наблюдения получаем, что (A+B+C) p -A p -B p -C p ={[(A+B)+C] p -(A+B) p -C p }+(A+B) p -A p -B p всегда делится на р ; (A+B+C+D) p -A p -B p -C p -D p всегда делится на р ; и вообще, (A+B+C+...+K) p -A p -B p -C p -...-K p всегда делится на р . Положим теперь в последнем выражении A=B=C=...=K=1 и возьмем количество этих чисел равным a . Получится, что a p -a делится на р , а это и есть теорема Ферма в более общей формулировке.
Следствие 2. (a+b) p a p +b p (mod p) .
Система шифрования RSA
Пусть ![]() и
и ![]() натуральные
числа. Функция
натуральные
числа. Функция ![]() , реализующая схему
RSA, устроена следующим образом
, реализующая схему
RSA, устроена следующим образом
| (1) |
Для дешифрования
сообщения ![]() достаточно решить сравнение
достаточно решить сравнение
| (2) |
При некоторых условиях на
![]() и
и
![]() это
сравнение имеет единственное решение
это
сравнение имеет единственное решение ![]() .
.
Для того,
чтобы описать эти условия и объяснить, как можно найти решение, нам потребуется
одна теоретико-числовая функция, так называемая функция Эйлера. Эта функция
натурального аргумента ![]() обозначается
обозначается ![]() и
равняется количеству целых чисел на отрезке от
и
равняется количеству целых чисел на отрезке от ![]() до
до ![]() , взаимно
простых с
, взаимно
простых с ![]() . Так
. Так ![]() и
и ![]() для любого простого числа
для любого простого числа ![]() и
натурального
и
натурального ![]() . Кроме того,
. Кроме того, ![]() для любых натуральных взаимно простых
для любых натуральных взаимно простых ![]() и
и ![]() .
Эти свойства позволяют легко вычислить значение
.
Эти свойства позволяют легко вычислить значение ![]() , если известно
разложение числа
, если известно
разложение числа ![]() на простые сомножители.
на простые сомножители.
Если
показатель степени ![]() в сравнении (2) взаимно
прост с
в сравнении (2) взаимно
прост с ![]() , то сравнение (2) имеет единственное решение. Для того, чтобы
найти его, определим целое число
, то сравнение (2) имеет единственное решение. Для того, чтобы
найти его, определим целое число ![]() , удовлетворяющее условиям
, удовлетворяющее условиям
| (3) |
Такое число
существует, поскольку ![]() , и притом
единственно. Здесь и далее символом
, и притом
единственно. Здесь и далее символом ![]() будет обозначаться
наибольший общий делитель чисел
будет обозначаться
наибольший общий делитель чисел ![]() и
и ![]() .
Классическая теорема Эйлера, см. [3], утверждает, что для каждого числа
.
Классическая теорема Эйлера, см. [3], утверждает, что для каждого числа ![]() , взаимно
простого с
, взаимно
простого с ![]() , выполняется сравнение
, выполняется сравнение ![]() и,
следовательно,
и,
следовательно,
| (4) |
Таким образом, в
предположении ![]() , единственное
решение сравнения (2) может быть найдено в виде
, единственное
решение сравнения (2) может быть найдено в виде
| (5) |
Если
дополнительно предположить, что число ![]() состоит из различных
простых сомножителей, то сравнение (5) будет выполняться и без предположения
состоит из различных
простых сомножителей, то сравнение (5) будет выполняться и без предположения ![]() .
Действительно, обозначим
.
Действительно, обозначим ![]() и
и ![]() . Тогда
. Тогда ![]() делится
на
делится
на ![]() , а из (2) следует, что
, а из (2) следует, что ![]() . Подобно (4),
теперь легко находим
. Подобно (4),
теперь легко находим ![]() . А
кроме того, имеем
. А
кроме того, имеем ![]() . Получившиеся сравнения в силу
. Получившиеся сравнения в силу ![]() дают
нам (5).
дают
нам (5).
Функция (1),
принятая в системе RSA, может быть вычислена достаточно быстро. Как это
сделать, мы обсудим чуть ниже. Пока отметим лишь, что обратная к ![]() функция
функция ![]() вычисляется по тем же правилам, что и
вычисляется по тем же правилам, что и
![]() , лишь с заменой показателя степени
, лишь с заменой показателя степени ![]() на
на ![]() . Таким
образом, для функции (1) будут выполнены указанные выше свойства а) и б).
. Таким
образом, для функции (1) будут выполнены указанные выше свойства а) и б).
Для
вычисления функции (1) достаточно знать лишь числа ![]() и
и ![]() . Именно они
составляют открытый ключ для шифрования. А вот для вычисления обратной функции
требуется знать число
. Именно они
составляют открытый ключ для шифрования. А вот для вычисления обратной функции
требуется знать число ![]() , оно и является
``секретом'' , о котором речь идет в пункте в). Казалось бы, ничего не стоит,
зная число
, оно и является
``секретом'' , о котором речь идет в пункте в). Казалось бы, ничего не стоит,
зная число ![]() , разложить его на простые сомножители, вычислить затем с помощью
известных правил значение
, разложить его на простые сомножители, вычислить затем с помощью
известных правил значение ![]() и, наконец, с
помощью (3) определить нужное число
и, наконец, с
помощью (3) определить нужное число ![]() . Все шаги этого
вычисления могут быть реализованы достаточно быстро, за исключением первого.
Именно разложение числа
. Все шаги этого
вычисления могут быть реализованы достаточно быстро, за исключением первого.
Именно разложение числа ![]() на простые множители и
составляет наиболее трудоемкую часть вычислений. В теории чисел несмотря на
многолетнюю ее историю и на очень интенсивные поиски в течение последних 20
лет, эффективный алгоритм разложения натуральных чисел на множители так и не
найден. Конечно, можно, перебирая все простые числа до
на простые множители и
составляет наиболее трудоемкую часть вычислений. В теории чисел несмотря на
многолетнюю ее историю и на очень интенсивные поиски в течение последних 20
лет, эффективный алгоритм разложения натуральных чисел на множители так и не
найден. Конечно, можно, перебирая все простые числа до ![]() , и, деля на них
, и, деля на них
![]() ,
найти требуемое разложение. Но, учитывая, что количество простых в этом
промежутке, асимптотически равно
,
найти требуемое разложение. Но, учитывая, что количество простых в этом
промежутке, асимптотически равно ![]() ,
находим, что при
,
находим, что при ![]() , записываемом 100 десятичными
цифрами, найдется не менее
, записываемом 100 десятичными
цифрами, найдется не менее ![]() простых
чисел, на которые придется делить
простых
чисел, на которые придется делить ![]() при разложении его на
множители. Очень грубые прикидки показывают, что компьютеру, выполняющему
миллион делений в секунду, для разложения числа
при разложении его на
множители. Очень грубые прикидки показывают, что компьютеру, выполняющему
миллион делений в секунду, для разложения числа ![]() таким
способом на простые сомножители потребуется не менее, чем
таким
способом на простые сомножители потребуется не менее, чем ![]() лет.
Известны и более эффективные способы разложения целых чисел на множители, чем
простой перебор простых делителей, но и они работают очень медленно. Таким
образом, название статьи М. Гарднера вполне оправдано.
лет.
Известны и более эффективные способы разложения целых чисел на множители, чем
простой перебор простых делителей, но и они работают очень медленно. Таким
образом, название статьи М. Гарднера вполне оправдано.
Авторы схемы
RSA предложили выбирать число ![]() в виде произведения
двух простых множителей
в виде произведения
двух простых множителей ![]() и
и ![]() , примерно
одинаковых по величине. Так как
, примерно
одинаковых по величине. Так как
| (6) |
то единственное условие
на выбор показателя степени ![]() в отображении (1) есть
в отображении (1) есть
| (7) |
Итак, лицо,
заинтересованное в организации шифрованной переписки с помощью схемы RSA,
выбирает два достаточно больших простых числа ![]() и
и ![]() . Перемножая
их, оно находит число
. Перемножая
их, оно находит число ![]() . Затем выбирается
число
. Затем выбирается
число ![]() , удовлетворяющее условиям (7), вычисляется с помощью (6) число
, удовлетворяющее условиям (7), вычисляется с помощью (6) число ![]() и
с помощью (3) - число
и
с помощью (3) - число ![]() . Числа
. Числа ![]() и
и ![]() публикуются,
число
публикуются,
число ![]() остается секретным. Теперь любой может отправлять зашифрованные с
помощью (3) сообщения организатору этой системы, а организатор легко сможет
дешифровывать их с помощью (5).
остается секретным. Теперь любой может отправлять зашифрованные с
помощью (3) сообщения организатору этой системы, а организатор легко сможет
дешифровывать их с помощью (5).
Для
иллюстрации своего метода Ривест, Шамир и Адлеман зашифровали таким способом
некоторую английскую фразу. Сначала она стандартным образом (a=01, b=02, ...,
z=26, пробел=00) была записана в виде целого числа ![]() , а затем зашифрована с
помощью отображения (1) при
, а затем зашифрована с
помощью отображения (1) при
![]()
и ![]() .
Эти два числа были опубликованы, причем дополнительно сообщалось, что
.
Эти два числа были опубликованы, причем дополнительно сообщалось, что ![]() ,
где
,
где ![]() и
и ![]() - простые числа,
записываемые соответственно
- простые числа,
записываемые соответственно ![]() и
и ![]() десятичными
знаками. Первому, кто дешифрует соответствующее сообщение
десятичными
знаками. Первому, кто дешифрует соответствующее сообщение
![]()
была обещана награда в 100$.
Эта история
завершилась спустя 17 лет в 1994 г., когда D. Atkins, M. Graff, A. K. Lenstra и
P. C. Leyland сообщили о дешифровке фразы, предложенной в [1]. Она1) была
вынесена в заголовок статьи, а соответствующие числа ![]() и
и ![]() оказались
равными
оказались
равными
![]()
Определение. Функция : R R (или, более общо, : C C ) называется мультипликативной если:
1). Функция определена всюду на N и существует а N такой, что ( а ) 0.
2). Для любых взаимно простых натуральных чисел а 1 и а 2 выполняется ( а 1 · а 2 ) = ( а 1 ) · ( а 2 ).
Пример 1. ( а ) = а s , где s - любое (хоть действительное, хоть комплексное) число. Проверка аксиом 1) и 2) из определения мультипликативной функции не составляет труда, а сам пример показывает, что мультипликативных функций по меньшей мере континуум, т.е. много.
Перечислим, кое-где доказывая, некоторые свойства мультипликативных функций. Пусть всюду ниже ( а ) - произвольная мультипликативная функция.
Свойство 1. (1) = 1.
Доказательство. Пусть а - то самое натуральное число, для которого
( а ) 0. Тогда ( а · 1) = ( а ) · (1) = ( а ).
Свойство 2.
![]() ,
,
где р 1 , р 2 ,..., р n - различные простые числа.
Доказательство очевидно.
Свойство 3. Обратно, мы всегда построим некоторую мультипликативную функцию ( a ), если зададим (1) = 1 и произвольно определим ( р ) для всех простых р и всех натуральных , а для остальных натуральных чисел доопределим функцию ( a ) используя равенство
![]() .
.
Доказательство сразу следует из основной теоремы арифметики.
Пример 2. Пусть (1) = 1 и ( р ) = 2 для всех р и . Тогда, для произвольного числа,
![]() .
.
Свойство 4. Произведение нескольких мультипликативных функций является мультипликативной функцией.
Доказательство. Сначала докажем для двух сомножителей: Пусть 1 и 2 - мультипликативные функции = 1 · 2 , тогда (проверяем аксиомы определения)
1) (1) = 1 (1) · 2 (1) = 1 и, кроме того, существует такое a (это a = 1), что ( a ) 0.
2) Пусть ( a , b ) = 1 - взаимно просты. Тогда
( a · b ) = 1 ( a · b ) · 2 ( a · b ) =
= 1 ( a ) 1 ( b ) 2 ( a ) 2 ( b ) =
= 1 ( a ) 2 ( a ) · 1 ( b ) 2 ( b ) = ( a ) ( b ).
Доказательство для большего числа сомножителей проводится стандартным индуктивным рассуждением.
Введем удобное обозначение. Всюду далее, символом
![]()
будем обозначать сумму чего-либо, в которой суммирование проведено по всем делителям d числа n . Следующие менее очевидные, чем предыдущие, свойства мультипликативных функций я сформулирую в виде лемм, ввиду их важности и удобства дальнейших ссылок.
Лемма 1. Пусть
![]()
- каноническое разложение числа a N , - любая мультипликативная функция. Тогда:
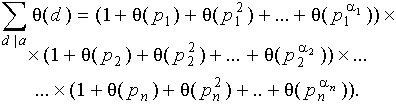
Если a = 1, то считаем правую часть равной 1.
Доказательство. Раскроем скобки в правой части. Получим сумму всех (без пропусков и повторений) слагаемых вида
![]() ,
,
где 0 k k , для всех k n . Так как различные простые числа заведомо взаимно просты, то
![]() ,
,
а это как раз то, что стоит в доказываемом равенстве слева.
Лемма 2. Пусть ( a ) - любая мультипликативная функция. Тогда
![]() ,
,
- также мультипликативная функция.
Доказательство. Проверим для ( a ) аксиомы определения мультипликативной функции.
1). ![]()
2). Пусть
![]()
и все р и q различны. Тогда, по предыдущей лемме, имеем: (благо, делители у чисел a и b различны)
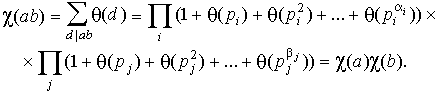
Пример 1. Число делителей данного числа.
Пусть ( а ) = а 0 1 - тождественная единица (заведомо мультипликативная функция). Тогда, если
![]() ,
,
то тождество леммы 1 пункта 13 принимает вид:
![]() ,
,
- это не что иное, как количество делителей числа a . По лемме 2 пункта 13, количество делителей ( a ) числа a есть мультипликативная функция.
Пример 2. Сумма делителей данного числа.
Пусть ( a ) = a 1 a - тождественная мультипликативная функция. Тогда, если
![]() ,
,
то тождество леммы 1 пункта 13 принимает вид:
![]()
|
|
|
сумма первых ( + 1) членов геометрической прогрессии |
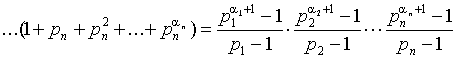
- сумма всех делителей числа a . По лемме 2 пункта 13, сумма всех делителей есть мультипликативная функция.
Пример 3. Функция Мебиуса.
Функция Мебиуса ( a ) - это мультипликативная функция, определяемая следующим образом: если p - простое число, то ( p ) = -1; ( p ) = 0, при > 1; на остальных натуральных числах функция доопределяется по мультипликативности.
Таким образом, если число a делится на квадрат натурального числа, отличный от единицы, то ( a ) = 0; если же a = p 1 p 2· · · p n (теоретик-числовик сказал бы на своем жаргоне: "если a свободно от квадратов"), то ( a ) = (-1) k , где k - число различных простых делителей a . Понятно, что (1) = (-1) 0 = 1, как и должно быть.
Лемма 1. Пусть ( a ) - произвольная мультипликативная функция,
![]() .
.
Тогда:
![]()
(при a = 1 считаем правую часть равной 1).
Доказательство. Рассмотрим функцию 1 ( x ) = ( x ) · ( x ). Эта функция мультипликативна, как произведение мультипликативных функций. Для 1 ( x ) имеем ( p - простое): 1 ( p ) = - ( x ); 1 ( p ) = 0, при > 1. Следовательно, для 1 ( x ) тождество леммы 1 пункта 13 выглядит так:
![]()
Следствие 1. Пусть ( d ) = d -1 = 1/ d (это, конечно, мультипликативная функция),
![]()
Тогда:
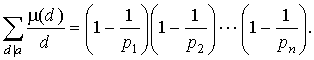
Пример 4. Функция Эйлера.
Функция Эйлера, пожалуй, самая знаменитая и "дары приносящая" функция из всех функций, рассматриваемых в этом пункте. Функция Эйлера ( a ) есть количество чисел из ряда 0, 1, 2,..., a - 1, взаимно простых с a . Полезность и практическое применение этой функции я продемонстрирую в следующих пунктах, а сейчас давайте поймем, как ее вычислять.
Лемма 2. Пусть
![]() .
.
Тогда:
1) 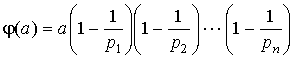 (формула
Эйлера);
(формула
Эйлера);
2) ![]()
в частности, ( p ) = p - p -1 , ( p ) = p - 1.
Доказательство. Пусть x пробегает числа 0, 1, 2,..., a - 1. Положим x = ( x , a ) - наибольший общий делитель. Тогда ( a ) есть число значений x , равных 1. Придумаем такую функцию ( x ), чтобы она была единицей, когда x единица, и была нулем в остальных случаях. Вот подходящая кандидатура:
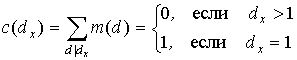
Последнее легко понять, если вспомнить лемму 1 из этого пункта и в ее формулировке взять ( d ) 1. Далее, сделав над собой некоторое усилие, можно усмотреть, что:
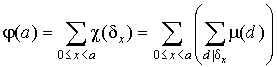
Поскольку справа сумма в скобках берется по всем делителям d числа x = ( x , a ), то d делит x и d делит a . Значит в первой сумме справа в суммировании участвуют только те x , которые кратны d . Таких x среди чисел 0, 1, 2,..., a - 1 ровно a / d штук. Получается, что:
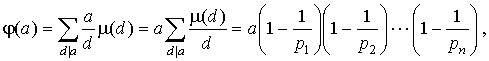
что и требовалось.
Пояснение для читателей, у которых предыдущие соображения не захотели укладываться в голову, например, из-за плохих погодных условий. Имеем
![]()
Зафиксируем некоторое d 0 такое, что d 0 делит a , d 0 делит x , x < a . Значит в сумме справа в скобках слагаемых ( d 0 ) ровно a / d 0 штук и ( a ) есть просто сумма
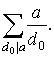
После этого, равенство

получается применением следствия из леммы 1 этого пункта. Должен признать, что приведенное доказательство формулы Эйлера и, в особенности, его последний момент с изменением порядка суммирования, объективно тяжеловаты для понимания. Но мы не боимся трудностей!
Второе утверждение леммы следует из первого внесением впереди стоящего множителя a внутрь скобок.
Оказывается, только что доказанная формула
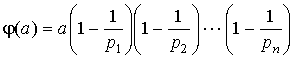
для вычисления функции Эйлера имеет ясный "физический смысл". Дело в том, что в ней отражено так называемое правило включений и исключений:
Правило включений и исключений. Пусть задано множество А и выделено k его подмножеств. Количество элементов множества А , которые не входят ни в одно из выделенный подмножеств, подсчитывается так: надо из общего числа элементов А вычесть количества элементов всех k подмножеств, прибавить количества элементов всех их попарных пересечений, вычесть количества элементов всех тройных пересечений, прибавить количества элементов всех пересечений по четыре и т.д. вплоть до пересечения всех k подмножеств.
Проиллюстрирую это правило на примере подсчета функции Эйлера для чисел вида
![]()
Посмотрите на рисунок 1.

Рис. 1.
Прямоугольник изображает множество всех целых чисел от 0 до a ; овал N 1 - множество чисел, кратных p 1 ; кружок N 2 - числа, кратные p 2 ; пересечение N 1,2 - множество чисел, делящихся одновременно на p 1 и p 2 , т.е. на p 1 p 2 ; числа вне овала и кружочка взаимно просты с a . Для подсчета числа чисел, взаимно простых с a , нужно из a вычесть количество чисел в N 1 и количество чисел в N 2 (их, соответственно, a / p 1 и a / p 2 штук), при этом общая часть N 1,2 (там a /( p 1 p 2 ) штук чисел) вычтется дважды, значит ее надо один раз прибавить (вот оно, "включение - исключение"!). В результате получим:
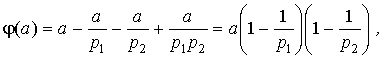
что я вам и утверждал. Мне кажется, что таким способом можно объяснить формулу Эйлера любому смышленому школьнику.
Кстати, любому смышленому школьнику вполне возможно объяснить и то, что при a > 2, ( a ) всегда число четное. Действительно, если k взаимно просто с a и k < a , то число a - k тоже меньше a , взаимно просто с a и не равно k . (Если бы a и a - k имели общий делитель, то их разность a - ( a - k ) = k тоже делилась бы на этот делитель, что противоречит взаимной простоте a и k .) Значит числа, взаимно простые с a разбиваются на пары k и a - k , следовательно, их четное число.
Из леммы 2 вытекают приятные следствия.
Следствие 2. Функция Эйлера мультипликативна.
Доказательство. Имеем:
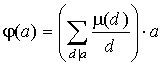
- произведение двух мультипликативных функций, первая из которых мультипликативна по лемме 2 пункта 13. Значит, ( a ) - мультипликативна.
Следствие
3.  .
.
Доказательство. Пусть
![]() .
.
Тогда, по лемме 1 пункта 13 имеем:
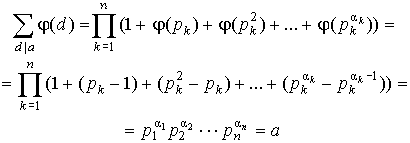 .
.
5 Китайская теорема об остатках
В этом пункте детально рассмотрим только сравнения первой степени вида
ax b(mod m),
оставив более высокие степени на съедение следующим пунктам. Как решать такое сравнение? Рассмотрим два случая.
Случай 1. Пусть а и m взаимно просты. Тогда несократимая дробь m/a сама просится разложиться в цепную дробь:
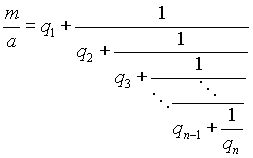
Эта цепная дробь, разумеется, конечна, так как m/a - рациональное число. Рассмотрим две ее последние подходящие дроби:
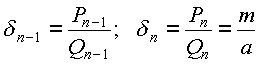 .
.
Вспоминаем (пункт 9) важное свойство числителей и знаменателей подходящих дробей: mQ n-1 -aP n-1 =(-1) n . Далее (слагаемое mQ n-1 , кратное m , можно выкинуть из левой части сравнения):
-aP n-1 (-1) n (mod m) т.е.
aP n-1 (-1) n-1 (mod m) т.е.
a[(-1) n-1 P n-1 b] b(mod m)
и единственное решение исходного сравнения есть:
x (-1) n-1 P n-1 b(mod m)
Пример. Решить сравнение 111x 75(mod 322).
Решение. (111, 322)=1. Включаем алгоритм Евклида:
322=11 · 2+100
111=100 · 1+11
100=11 · 9+1
11=1 · 11
(В равенствах подчеркнуты неполные частные.) Значит, n=4 , а соответствующая цепная дробь такова:
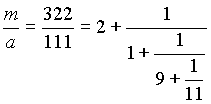
Посчитаем числители подходящих дробей, составив для этого стандартную таблицу:
| 0 | 2 | 1 | 9 | 11 | |
| P n | 1 | 2 | 3 | 29 | 322 |
Числитель предпоследней подходящей дроби равен 29, следовательно, готовая формула дает ответ: x (-1) 3 29 75 -2175 79(mod 322)
Ох уж эти мне теоретико-числовые рассуждения из разных учебников, продиктованные традицией изложения и необходимостью обязательно использовать ранее изложенную теорию! О чем идет речь в нескольких строках выше? Дано сравнение ax b(mod m) , где a и m взаимно просты. Ну возьмите вы алгоритм Евклида, найдите те самые пресловутые u , v Z такие, что au+vm=1 , умножьте это равенство на b : aub+vmb=b , откуда немедленно следует: aub b(mod m) . Значит решением исходного сравнения является x ub(mod m) . Собственно, и все. Поворчал.
Случай 2. Пусть (a,m)=d . В этом случае, для разрешимости сравнения ax b(mod m) необходимо, чтобы d делило b , иначе сравнение вообще выполняться не может. Действительно, ax b(mod m) бывает тогда, и только тогда, когда ax- b делится на m нацело, т.е. ax- b=t · m ,
t Z , откуда b=ax- t m , а правая часть последнего равенства кратна d .
Пусть b=db 1 , a=da 1 , m=dm 1 . Тогда обе части сравнения xa 1 d b 1 d(mod m 1 d) и его модуль поделим на d :
xa 1 b 1 (mod m 1 ) ,
где уже а 1 и m 1 взаимно просты. Согласно случаю 1 этого пункта, такое сравнение имеет единственное решение x 0 :
x x 0 (mod m 1 ) (*)
По исходному модулю m , числа (*) образуют столько решений исходного сравнения, сколько чисел вида (*) содержится в полной системе вычетов: 0,1,2,..., m-2, m-1 . Очевидно, что из чисел x=x 0 +t m в полную систему наименьших неотрицательных вычетов попадают только x 0 , x 0 +m 1 , x 0 +2m 1 , ..., x 0 +(d-1)m 1 , т.е. всего d чисел. Значит у исходного сравнения имеется d решений.
Подведем итог рассмотренных случаев в виде следующей теоремы
Теорема 1. Пусть (a,m)=d . Если b не делится на d , сравнение ax b(mod m) не имеет решений. Если b кратно d , сравнение ax b(mod m) имеет d штук решений.
Пример. Решить сравнение 111x 75(mod 321) .
Решение. (111,321)=3 , поэтому поделим сравнение и его модуль на 3:
37x 25(mod 107) и уже (37,107)=1 .
Включаем алгоритм Евклида (как обычно, подчеркнуты неполные частные):
107=37 2+33
37=33 1+4
33=4 8+1
4=1 4
Имеем n=4 и цепная дробь такова:
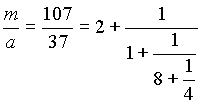
Таблица для нахождения числителей подходящих дробей:
| q n | 0 | 2 | 1 | 8 | 4 |
| P n | 1 | 2 | 3 | 26 | 107 |
Значит, x (-1) 3 26 25 -650(mod 107) -8(mod 107) 99(mod 107) .
Три решения исходного сравнения:
x 99(mod 321), x 206(mod 321), x 313(mod 321) ,
и других решений нет.
Теорема 2. Пусть m>1, (a,m)=1 Тогда сравнение ax b(mod m) имеет решение: x ba (m)-1 (mod m) .
Доказательство. По теореме Эйлера, имеем: a (m) 1(mod m) , следовательно, a ba (m)-1 b(mod m) .
Пример. Решить сравнение 7x 3(mod 10) . Вычисляем:
(10)=4; x 3 7 4-1 (mod 10) 1029(mod 10) 9(mod 10) .
Видно, что этот способ решения сравнений хорош (в смысле минимума интеллектуальных затрат на его осуществление), но может потребовать возведения числа а в довольно большую степень, что довольно трудоемко. Для того, чтобы как следует это прочувствовать, возведите самостоятельно число 24789 в степень 46728.
Теорема 3. Пусть р – простое число, 0<a<p . Тогда сравнение ax b(mod p) имеет решение:
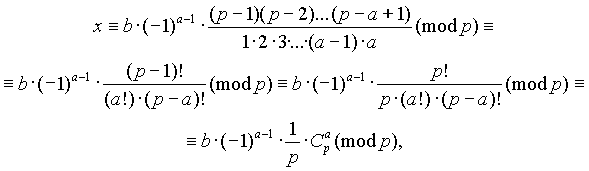
где C a p – биномиальный коэффициент.
Доказательство непосредственно следует из очевидного сравнения
![]()
которое нужно почленно поделить на взаимно простое с модулем число 1 2 3 ... a-1 .
Пример. Решить сравнение 7x 2(mod 11) . Вычисляем:
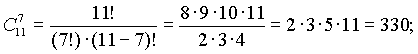
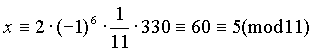
На этом пункт 19 можно было бы и закончить, но невозможно, говоря о решении сравнений первой степени, обойти стороной вопрос о решении систем сравнений первой степени. Дело в том, что умение решать простейшие системы сравнений не только является неотъемлемой частью общечеловеческой культуры, позволяющей гражданину не падать в ямы, расщелины и открытые люки. Такое умение, кроме всего прочего, пригодится нам при изучении сравнений произвольной степени, о которых пойдет речь в следующих пунктах.
Лемма 1 (Китайская теорема об остатках). Пусть дана простейшая система сравнений первой степени:
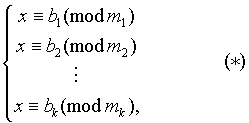
где m 1 ,m 2 ,...,m k попарно взаимно просты. Пусть, далее, m 1 m 2 ...m k =M s m s ; M s M s 1(mod m s ) (Очевидно, что такое число M s всегда можно подобрать хотя бы с помощью алгоритма Евклида, т.к. (m s ,M s )=1 ); x 0 =M 1 M 1 b 1 +M 2 M 2 b 2 +...+M k M k b k . Тогда система (*) равносильна одному сравнению
x x 0 (mod m 1 m 2 ...m k ) ,
т.е. набор решений (*) совпадает с набором решений сравнения x x 0 (mod m 1 m 2 ...m k ) .
Доказательство. Имеем: m s делит M j , при s j. Следовательно, x 0 M s M s b s (mod m s ) , откуда x 0 b s (mod m s ) . Это означает, что система (*) равносильна системе
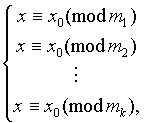
которая, очевидно, в свою очередь, равносильна одному сравнению x x 0 (mod m 1 m 2 ...m k ) .
В следующей лемме, для краткости формулировки, сохранены обозначения леммы 1.
Лемма 2. Если b 1 ,b 2 ,...,b k пробегают полные системы вычетов по модулям m 1 ,m 2 ,...,m k соответственно, то x 0 пробегает полную систему вычетов по модулю m 1 m 2 ...m k .
Доказательство. Действительно, x 0 =A 1 b 1 +A 2 b 2 +...+A k b k пробегает m 1 m 2 ...m k различных значений. Покажем, что все они попарно не сравнимы по модулю m 1 m 2 ...m k .
Ну пусть оказалось, что
A 1 b 1 +A 2 b 2 +...+A k b k A 1 b' 1 +A 2 b' 2 +...+A k b' k (mod m 1 m 2 ...m k )
Значит,
A 1 b 1 +A 2 b 2 +...+A k b k A 1 b' 1 +A 2 b' 2 +...+A k b' k (mod m s )
для каждого s , откуда
M s M s b s M s M s b' s
Вспомним теперь, что M s M s 1(mod m s ) , значит M s M s 1+m s t , откуда (M s M s ,m s )=1 . Разделив теперь обе части сравнения
M s M s b s M s M s b' s
на число M s M s , взаимно простое с модулем, получим, что b s b' s (mod m s ) , т.е. b s =b' s для каждого s .
Итак, x 0 пробегает m 1 m 2 ...m k различных значений, попарно не сравнимых по модулю m 1 m 2 ...m k , т.е. полную систему вычетов.
Формулировка для колец
Пусть ![]() - коммутативные ассоциативные кольца с единицей,
- коммутативные ассоциативные кольца с единицей, ![]() сюрьективные гомоморфизмы, обладающие свойством
сюрьективные гомоморфизмы, обладающие свойством ![]() для всех
для всех ![]() . Тогда
гомоморфизм
. Тогда
гомоморфизм ![]() , заданный формулой
, заданный формулой
![]()
является сюрьективным. Более того, Φ опеределяет изоморфизм
![]() .
.
Если положить
![]() ,
, ![]() и определить гомоморфизмы следующим
образом
и определить гомоморфизмы следующим
образом
![]()
то мы получим арифметическую версию теоремы.
Также часто
встречается следующая эквивалентная формулировка для колец, где Bi имеют форму A
/ Ii, φi
являются естественными проекциями на A / Ii
и требуется, чтобы Ii + Ij
= A для любых ![]() .
.
Заключение
История арифметики остатков начинается с исследований К.Ф. Гаусса, который впервые стал рассматривать сравнения. В дальнейшем была обнаружена связь теории сравнений с астрономическими задачами (китайская теорема об остатках). В результате многочисленных исследований теория остатков была распространена на кольца произвольной природы. В последнее время обнаружилось приложение этой теории в криптографии. В дипломной работе изложена теория остатков на современном алгебраическом языке.
Список использованных источников
1. С. Ленг, Алгебра, М., 1968
2. С. Коунтинхо, Введение в теорию чисел. Алгоритм RSA, М. 2001
3. А.И. Кострикин, Введение в алгебру, М., 2000
4. О. Зарисский, Коммутативная алгебра, т.1., М., 1963