Рефераты по авиации и космонавтике
Рефераты по административному праву
Рефераты по безопасности жизнедеятельности
Рефераты по арбитражному процессу
Рефераты по архитектуре
Рефераты по астрономии
Рефераты по банковскому делу
Рефераты по сексологии
Рефераты по информатике программированию
Рефераты по биологии
Рефераты по экономике
Рефераты по москвоведению
Рефераты по экологии
Краткое содержание произведений
Рефераты по физкультуре и спорту
Топики по английскому языку
Рефераты по математике
Рефераты по музыке
Остальные рефераты
Рефераты по биржевому делу
Рефераты по ботанике и сельскому хозяйству
Рефераты по бухгалтерскому учету и аудиту
Рефераты по валютным отношениям
Рефераты по ветеринарии
Рефераты для военной кафедры
Рефераты по географии
Рефераты по геодезии
Рефераты по геологии
Рефераты по геополитике
Рефераты по государству и праву
Рефераты по гражданскому праву и процессу
Рефераты по кредитованию
Рефераты по естествознанию
Рефераты по истории техники
Рефераты по журналистике
Рефераты по зоологии
Рефераты по инвестициям
Рефераты по информатике
Исторические личности
Рефераты по кибернетике
Рефераты по коммуникации и связи
Рефераты по косметологии
Рефераты по криминалистике
Рефераты по криминологии
Рефераты по науке и технике
Рефераты по кулинарии
Рефераты по культурологии
Контрольная работа: Прогноз среднего значения цены
Контрольная работа: Прогноз среднего значения цены
Задача 1
Магазин торгует подержанными автомобилями. Статистика их потребительских цен накапливается в базе данных. В магазин пригоняют на продажу очередную партию небольших однотипных автомобилей. Как назначить их цену? Статистический подход позволяет дать прогноз среднего значения цены и доверительных интервалов для него.
Цена автомобиля зависит от множества факторов. К числу объясняющих переменных можно отнести, например, модель автомобиля, фирму-производитель, регион производства (Европа, США, Япония), объем двигателя, фирму-производитель, регион производства (Европа, США, Япония), объем производителя, количество цилиндров, время разгона до 100 км/час, пробег, потребление горючего, год выпуска и т.д. Первые из названных переменных очень важны при ценообразовании, но они – качественные. Традиционный регрессионный анализ, рассматриваемый в этом задании, предназначен для количественных данных. Поэтому, не претендуя на высокую точность, не будем включать их в эконометрическую модель. Сделаем выборку, например, только для автомобилей одной фирмы-производителя. Пусть, например, оказалось, что продано n= 16 таких автомобилей. Для упрощения выберем из базы данных цены yi (i = 1......16) проданных автомобилей и только две объясняющие переменные: возраст хi1 (i = 1, …..16) в годах и мощность двигателя хi2 (i = 1, ….16) в лошадиных силах. Выборка представлена в таблице:
| I номер |
yi , цена, тыс. у.е. |
хi1 возраст,лет |
хi2, мощность двигателя |
| 11 | 5,0 | 155 | |
| 2 | 6 | 7,0 | 87 |
| 3 | 9,8 | 5,0 | 106 |
| 4 | 11 | 4,0 | 89 |
| 5 | 12,3 | 4,0 | 133 |
| 6 | 8,7 | 6,0 | 94 |
| 7 | 9,3 | 5,0 | 124 |
| 8 | 10,6 | 5,0 | 105 |
| 9 | 11,8 | 4,0 | 120 |
| 10 | 10,6 | 4,0 | 107 |
| 11 | 5,2 | 7,0 | 53 |
| 12 | 8,2 | 5,0 | 80 |
| 13 | 6,5 | 6,0 | 67 |
| 14 | 5,7 | 7,0 | 73 |
| 15 | 7,9 | 6,0 | 100 |
| 16 | 10,5 | 4,0 | 118 |
1. Построить поля рассеяния между ценой y и возрастом автомобиля х1, между ценой y и мощностью автомобиля x2. На основе их визуального анализа выдвинуть гипотезу о виде статистической зависимости y от х1 и y от х2. Найти точечные оценки независимых параметров
а0а1 модели y = а0 + а1 х1 + ε и
β1β2 модели y = β0 + а1 х1 + δ
2. Проанализировать тесноту линейной связи между ценой и возрастом автомобиля, а также ценой и мощностью двигателя х2. Для этого рассчитать коэффициенты парной корреляции ryx1 и ryx2 и проверить их отличие от нуля при уровне значимости α = 0,1.
3. Проверить качество оценивания моделей на основе коэффициента детерминации, F- и t- критериев при уровне значимости α = 0,05 и α = 0,10.
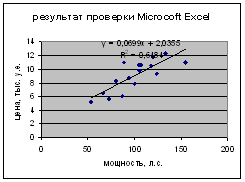
4. Проверить полученные результаты с помощью средств Microcoft Excel.
5. С помощью уравнений регрессии рассчитать доверительные интервалы для среднего значения цены, соответствующие доверительной вероятности 0,9. Изобразить графически поля рассеяния, линии регрессии и доверительные полосы.
На продажу поступила очередная партия однотипных автомобилей. Их возраст х1 равен 3 года. Мощность двигателя х2 = 165 л.с. Рассчитать точечный и интервальный прогноз среднего значения цены поступивших автомобилей по моделям y = а0 + а1 х1 + ε и y = β0 + а1 х1 + δ с доверительной вероятностью 0,9.
Решение:
На основе поля рассеяния, построенного на основе табл. 1, выдвигаем гипотезу о том, что зависимость цены y от возраста автомобиля x1 описывается линейной моделью вида
y = а0 + а1 х1 + ε
где а0 и а1 – неизвестные постоянные коэффициенты, а ε – случайная переменная (случайное возмущение), отражающая влияние неучтенных факторов и погрешностей измерений.
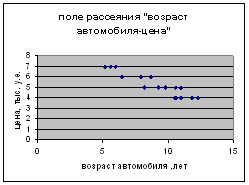
Рисунок 1 – Поле рассеяния «возраст автомобиля-цена»
Аналогично, на основе анализа поля рассеяния (рис. 2), также построенного на основе таблицы 1, выдвигаем гипотезу о том, что зависимость цены y от мощности автомобиля x2 описывается линейной моделью вида
y = β0 + β1 х1 + δ
где β0 и β1 – неизвестные постоянные коэффициенты, а ε – случайная переменная (случайное возмущение), отражающая влияние неучтенных факторов и погрешностей измерений.
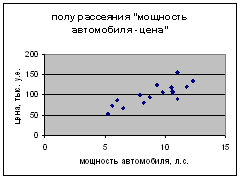
Рисунок 2 – Поле рассеяния «мощность автомобиля-цена»
На основе табл. 1 исходных данных для вычисления оценок параметров моделей составляется вспомогательная табл. 1.1. Воспользуемся формулами и левой частью таблицы 1.1. для нахождения оценок а0 и а1.
Так как n = 16, получаем
![]() = 145/16=9.0625
= 145/16=9.0625
![]() = 84.0/16=5.25
= 84.0/16=5.25
![]() = 27.5625
= 27.5625
![]() = 365
= 365
![]() = 460
= 460
| i |
yi |
xi1 |
xi12 |
xi1 yi |
yi2 |
i |
yi |
xi2 |
xi22 |
xi2 yi |
| 11 | 5.0 | 25 | 55 | 121 | 1 | 11 | 155 | 24025 | 1705 | |
| 2 | 6 | 7.0 | 49 | 42 | 36 | 2 | 6 | 87 | 7569 | 522 |
| 3 | 9,8 | 5.0 | 25 | 49 | 96,04 | 3 | 9,8 | 106 | 11236 | 1038,8 |
| 4 | 11 | 4.0 | 16 | 44 | 121 | 4 | 11 | 89 | 7921 | 979 |
| 5 | 12,3 | 4.0 | 16 | 49,2 | 151,29 | 5 | 12,3 | 133 | 17689 | 1635,9 |
| 6 | 8,7 | 6.0 | 36 | 52,2 | 75,69 | 6 | 8,7 | 94 | 8836 | 817,8 |
| 7 | 9,3 | 5.0 | 25 | 46,5 | 86,49 | 7 | 9,3 | 124 | 15376 | 1153,2 |
| 8 | 10,6 | 5.0 | 25 | 53 | 112,36 | 8 | 10,6 | 105 | 11025 | 1113 |
| 9 | 11,8 | 4.0 | 16 | 47,2 | 139,24 | 9 | 11,8 | 120 | 14400 | 1416 |
| 10 | 10,6 | 4.0 | 16 | 42,4 | 112,36 | 10 | 10,6 | 107 | 11449 | 1134,2 |
| 11 | 5,2 | 7.0 | 49 | 36,4 | 27,04 | 11 | 5,2 | 53 | 2809 | 275,6 |
| 12 | 8,2 | 5.0 | 25 | 41 | 67,24 | 12 | 8,2 | 80 | 1600 | 656 |
| 13 | 6,5 | 6.0 | 36 | 39 | 42,25 | 13 | 6,5 | 67 | 4489 | 435,5 |
| 14 | 5,7 | 7.0 | 49 | 39,9 | 32,49 | 14 | 5,7 | 73 | 5329 | 416,1 |
| 15 | 7,9 | 6.0 | 36 | 47,4 | 62,41 | 15 | 7,9 | 100 | 10000 | 790 |
| 16 | 10,5 | 4.0 | 16 | 42 | 110,25 | 16 | 10,5 | 118 | 13924 | 1239 |
| Сумма | 145,1 | 84.0 | 460 | 726,2 | 1393,15 | 145,1 | 1611 | 167677 | 15327,1 |
Следовательно,
а1 = ![]()
а0 = 9,0625- (-1,844) * 5.25 = 18,74
Таким образом,
![]()
Аналогично находятся оценки коэффициентов второй регрессионной модели y = β0 + β1 х1 + δ. При этом используется правая часть таблицы
![]() = 1611/16=100,6875
= 1611/16=100,6875
![]() = 10137.97
= 10137.97
![]() = 153271,1
= 153271,1
![]() = 167677
= 167677
β1 = ![]()
β 0 = 9,0625- 0,0099 * 100.6875= 2.0355
Окончательно получаем:
![]()
Подставляем соответствующие значения в формулу:
ryx = 
ryx1 = ![]() = 0,915
= 0,915
ryx2 = ![]() = 0.8
= 0.8
В нашей задаче t0.95;14 = 1,761
Для ryx1 получаем
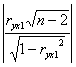 =
= 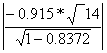 = 0,955
<1.761
= 0,955
<1.761
Условие не выполняется, следовательно, коэффициент парной корреляции не значим, гипотеза отвергается, между переменными отсутствует линейная связь
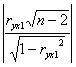 =
= 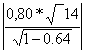 = 4.98>1.761
= 4.98>1.761
Условие выполняется, следовательно, коэффициент парной корреляции значимый, гипотеза подтверждается, между переменными существует сильная линейная связь
Коэффициент парной корреляции ryx связан с коэффициентом а1 уравнения регрессии
![]() следующим образом
следующим образом
ryx = a1 Sx/Sy
где Sx, Sy – выборочные среднеквадратичные отклонения случайных переменных х и y соответственно, рассчитывающиеся по формулам:
Sx1 = √ Sx12
Sx12 = 1/n ∑(xi
- ![]() )2
)2
Sy = √ Sy2
Sy2 = 1/n ∑(yi
- ![]() )2
)2
ryx1 = 0,915
ryx2 = 0,8
R2 = ryx12 = 0,8372
Вариация на 83,72 % объясняется вариацией возраста автомобиля
R2 = ryx22 = 0,64
Вариация на 64 % объясняется вариацией мощности двигателя автомобиля
Рассчитаем фактическое значение F- статистики Фишера по формуле:
F=![]()
F=![]() = 0,768 для
зависимости y от х1
= 0,768 для
зависимости y от х1
F=![]() = 0,285для
зависимости y от х2
= 0,285для
зависимости y от х2
Fт = 4,6
Поэтому для зависимостей y от х1 и y от х2 выполняется неравенство
Fт <Fф
гипотеза отклоняется и признается статистическая значимость уравнения регрессии.
Для оценки статистической значимости коэффициентов регрессии используется t-критерий Стьюдента.
Для зависимости y от х1:
![]() = √F = √0,768 = 0,876
= √F = √0,768 = 0,876
Поскольку это значение меньше 1,761, то принимаем нулевую гипотезу равенства нулю а1
Для зависимости y от х2:
![]() = √F = √0,285 = 0,533
= √F = √0,285 = 0,533
Поскольку это значение меньше 1,761, то принимаем нулевую гипотезу равенства нулю а1
Проверка с помощью Microsoft Excel
| Оценка параметра а1 | -1,87237 | Оценка параметра а0 | 18,89868 |
| Среднеквадратическое отклонение | 0,200234 | Среднеквадратическое отклонение а0 | 1,073633 |
|
Коэффициент детерминации R2 |
0,861987 | Среднеквадратическое отклонение y | 0,872798 |
| F-Статистика | 87,43972 | Число степеней свободы | 14 |
| Регрессионная сумма квадратов | 66,60951 | Остаточная сумма квадратов | 10,66487 |
| Оценка параметра а1 | 0,0698523 | Оценка параметра а0 | 2,0354973 |
| Среднеквадратическое отклонение | 0,013746 | Среднеквадратическое отклонение а0 | 1,4271948 |
|
Коэффициент детерминации R2 |
0,648444 | Среднеквадратическое отклонение y | 1,3929996 |
| F-Статистика | 25,822959 | Число степеней свободы | 14 |
| Регрессионная сумма квадратов | 50,108105 | Остаточная сумма квадратов | 27,16627 |
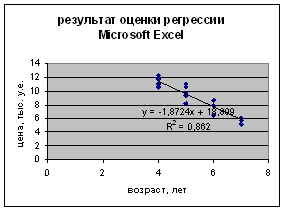
Рассчитаем доверительный интервал среднего значения цены для y = a0 + a1x1/
: ŷв.н. = ŷ(х0) ± t1-α/2,n-2Sŷ,
где ув, ун – соответственно верхняя и нижняя границы
доверительного интервала;
ŷ(х0) – точечный прогноз;
t1-α/2,n-2 –квантиль распределения Стьюдента;
(1-α/2) – доверительная верояность;
(n-2) – число степеней свободы;
: ŷв.н. = ŷ(х0) ± t1-α/2,n-2Sŷ,
ta = 2,57
Доверительный интервал для уn:
Нижняя граница интервала:
![]() = 18,74-1,844*5 = 9,52
= 18,74-1,844*5 = 9,52
Верхняя граница интервала:
![]() = 18,74-1,844*7 = 5,832
= 18,74-1,844*7 = 5,832
![]()
Sx12 = 1/n ∑(xi
- ![]() )2 = 19/16 = 1,1875
)2 = 19/16 = 1,1875
Sx1 = 1,089
|
xi1 |
xi1 - хср1 |
(xi1 - хср1)2 |
х2 |
х1х2 |
| 5.0 | -0,25 | 0,0625 | 155 | 775 |
| 7.0 | 1,75 | 3,0625 | 87 | 609 |
| 5.0 | -0,25 | 0,0625 | 106 | 530 |
| 4.0 | -1,25 | 1,5625 | 89 | 356 |
| 4.0 | -1,25 | 1,5625 | 133 | 532 |
| 6.0 | 0,75 | 0,5625 | 94 | 564 |
| 5.0 | -0,25 | 0,0625 | 124 | 620 |
| 5.0 | -0,25 | 0,0625 | 105 | 525 |
| 4.0 | -1,25 | 1,5625 | 120 | 480 |
| 4.0 | -1,25 | 1,5625 | 107 | 428 |
| 7.0 | 1,75 | 3,0625 | 53 | 371 |
| 5.0 | -0,25 | 0,0625 | 80 | 400 |
| 6.0 | 0,75 | 0,5625 | 67 | 402 |
| 7.0 | 1,75 | 3,0625 | 73 | 511 |
| 6.0 | 0,75 | 0,5625 | 100 | 600 |
| 4.0 | -1,25 | 1,5625 | 118 | 472 |
| 19 | 8175 |
myx= S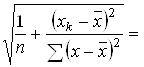 1,089*√1/16 + 1,5625/19 = 0,414
1,089*√1/16 + 1,5625/19 = 0,414
5,832 – 2,57*0,414 ≤ yn ≤ 5,832 + 2,57*0,414
На продажу поступила очередная партия однотипных автомобилей. Их возраст xp1 = 3 года. Мощность двигателя xp2 = 165 л.с.
Рассчитаем точечный и интервальный прогноз среднего значения цены поступивших автомобилей по первой парной регрессионной модели
y = β0 + β1 х1 + δ
Подставляем xp1
в уравнение регрессии: ![]()
Получим точечный интервальный прогноз среднего цены.
![]() (xp1)
= 18,74 – 1,844*3 = 13,208 тыс. у.е.
(xp1)
= 18,74 – 1,844*3 = 13,208 тыс. у.е.
Подставляем точечный интервальный прогноз среднего цены![]() (xp1) = 12,3 тыс. и xp1 = 3 года в уравнения границ доверительного интервала
регрессии. Получим интервальный прогноз с доверительной вероятностью 0,9
(xp1) = 12,3 тыс. и xp1 = 3 года в уравнения границ доверительного интервала
регрессии. Получим интервальный прогноз с доверительной вероятностью 0,9
ŷв.н. = 13,208±2,57*0,414 или ŷн = 12,14 тыс. у.е.,
ŷв = 14,27 тыс. у.е.
Задача 2
Найти по методу наименьших квадратов оценки коэффициентов множественной регрессионной модели
y = а0 + а1 х1 + а2 х2 +ε
Проверить качество оценивания моделей на основе коэффициента детерминации и F-критерия. Пояснить их содержательный смысл.
Проверить полученные в заданиях результаты с помощью средств Microcoft Excel.
Рассчитать точечный и интервальный прогноз среднего значения цены поступивших автомобилей по множественной модели y = а0 + а1 х1 + а2 х2 +ε с доверительной вероятностью 0,9. Как в задаче 1, возраст поступивших автомобилей х1 = 3 года, мощность двигателя х2 = 165 л.с.
На основе полученных в задачах 1-2 статистических характеристик провести содержательную интерпретацию зависимости цены автомобиля от возраста и мощности двигателя.
Сумма произведений ∑х1х2 равна: 8175
ХТХ =  ХТY =
ХТY =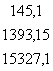
Найдем матрицу (Хт Х), обратную матрице ХТХ.
Для этого сначала вычислим определитель.
ХТХ = 16*460*167667+1611*84*8175+1611*84*8175-1611*460*1611-84*84*167677-16*8175*8175 = 1234102720+1106273700+1106273700-1193847660-1183128912-1069290000 = 383548
Определим матрицу алгебраических дополнений
Задача 3
В таблице представлены ежегодные данные объема продаж автомагазина. Построить график во времени. Выдвинуть гипотезу о наличии тренда. Оценить неизвестные параметры линейной трендовой модели z = а0 а1t +ε с методом наименьших квадратов.
Таблица 2 Ежегодные объемы продаж
| t годы | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
|
zt, продажи, тыс.у.е. |
350 | 314 | 300 | 293 | 368 | 393 | 339 | 443 | 467 | 457 | 488 | 424 |
Для найденного уравнения тренда построить доверительную полосу при уровне доверия 0,9. Изобразить графически точечный и интервальный прогноз среднего объема продаж.
В таблице 3 объемы продаж zt в тыс. у.е. детализированы по месяцам. Построить график объема продаж во времени. Выдвинуть гипотезу о наличии линейного тренда и сезонных колебаний объема продаж:
z1 = а0 а1t + а2cos (2πt/12) + а3sin (2πt/12) + εt
Оценить параметры этой модели методом наименьших квадратов.
По уравнению трендово-сезонной модели найти точечный прогноз среднего объема продаж на 12 месяцев и интервальный прогноз среднего объема продаж на 1 месяц вперед при доверительной вероятности 0,9.
Ежемесячные объемы продаж
| t,годы |
Zt |
t |
ytt |
t2 |
| 1 | 2 | 3 | 4 | 5 |
| 1 | 350 | 1 | 350 | 1 |
| 2 | 314 | 2 | 728 | 4 |
| 3 | 300 | 3 | 900 | 9 |
| 4 | 293 | 4 | 1172 | 16 |
| 5 | 368 | 5 | 1840 | 25 |
| 6 | 393 | 6 | 2358 | 36 |
| 7 | 339 | 7 | 2373 | 49 |
| 8 | 443 | 8 | 3544 | 64 |
| 9 | 467 | 9 | 3736 | 81 |
| 10 | 457 | 10 | 4570 | 100 |
| 11 | 488 | 11 | 5368 | 121 |
| 12 | 424 | 12 | 5088 | 144 |
| 78 | 4636 | 78 | 32027 | 650 |
∑t = ½*12 (12+1) = 78
∑t2 = 1/6 *12 (12+1) (24+1)= 650
а0 = ![]() 515294/1716=283,61
515294/1716=283,61
а1 =![]() =
22716/1716=15,804
=
22716/1716=15,804
Следовательно, уравнение тренда (регрессии) будет иметь вид:
y= 283,61+15,84t
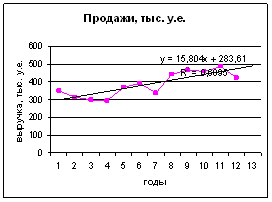
Доверительный интервал для линейного тренда находится по формуле:
ŷв.н. = ŷ(х0) ± t1-α/2,n-2Sŷ,
где ув, ун – соответственно верхняя и нижняя границы
доверительного интервала;
ŷ(х0) – точечный прогноз;
t1-α/2,n-2 –квантиль распределения Стьюдента;
(1-α/2) – доверительная верояность;
(n-2) – число степеней свободы;
ŷв.н. = ŷ(х0) ± t1-α/2,n-2Sŷ,
ta = 2,35
Доверительный интервал для уn:
Нижняя граница интервала:
y= 300.29+13.24t = 300,29+13,24*293 = 4179,61
Верхняя граница интервала:
y= 300.29+13.24t = 300,29+13,24*488= 6761,41
![]()
Sx12 = 1/n ∑(xi
- ![]() )2 = 51804,7/12 = 4317,06
)2 = 51804,7/12 = 4317,06
Sx1 = 65,704
zср = 386.33
| z |
zi - zср |
(zi - zi ср)2 |
| 350 | -36.33 | 1319,87 |
| 314 | -72.33 | 5231,63 |
| 300 | -86.33 | 7452,89 |
| 293 | -93.33 | 8710,49 |
| 368 | -18.33 | 335,99 |
| 393 | 6.67 | 44,49 |
| 339 | -47.33 | 2240,13 |
| 443 | 56.67 | 3211,49 |
| 467 | 80.67 | 6507,65 |
| 457 | 70.67 | 4994,25 |
| 488 | 101.67 | 10336,79 |
| 424 | 37.67 | 1419,03 |
| 4636 | 24624 | 51804,7 |
myx= S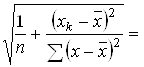 65,704*√1/12+ 24624/51804,7 =
36,71
65,704*√1/12+ 24624/51804,7 =
36,71
65,704 – 2,35*36,71 ≤ yn ≤ 65,704 + 2,35*36,71
Точечный прогноз среднего значения продаж по линейному тренду находится следующим образом:
ŷв.н. = 283,61+15,84*13 = 489,53
Окончательно получаем интервальный прогноз продаж
ŷв.н. = 489,5 ±2,353*36,71
Или ŷв= 489,5 ±2,353*36,71 = 575,89
Или ŷн= 489,5 ±2,353*36,71 = 403,12
Задача 4
Для регрессионных моделей:
y = а0 + а1 х1 + а2 х2 +ε
z1 = а0 а1t + а2cos (2πt/12) + а3sin (2πt/12) + εt
проверить наличие или отсутствие автокорреляции, используя критерий Дарбина-Уотсона при уровне значимости α = 0,05.
Для регрессионной модели y = а0 + а1 х1 + а2 х2 +ε
Проверить наличие или отсутствие мультиколлинеарности, используя критерии xи-квадрат (χ2) при уровне значимости α = 0,05.