
Рефераты по авиации и космонавтике
Рефераты по административному праву
Рефераты по безопасности жизнедеятельности
Рефераты по арбитражному процессу
Рефераты по архитектуре
Рефераты по астрономии
Рефераты по банковскому делу
Рефераты по сексологии
Рефераты по информатике программированию
Рефераты по биологии
Рефераты по экономике
Рефераты по москвоведению
Рефераты по экологии
Краткое содержание произведений
Рефераты по физкультуре и спорту
Топики по английскому языку
Рефераты по математике
Рефераты по музыке
Остальные рефераты
Рефераты по биржевому делу
Рефераты по ботанике и сельскому хозяйству
Рефераты по бухгалтерскому учету и аудиту
Рефераты по валютным отношениям
Рефераты по ветеринарии
Рефераты для военной кафедры
Рефераты по географии
Рефераты по геодезии
Рефераты по геологии
Рефераты по геополитике
Рефераты по государству и праву
Рефераты по гражданскому праву и процессу
Рефераты по кредитованию
Рефераты по естествознанию
Рефераты по истории техники
Рефераты по журналистике
Рефераты по зоологии
Рефераты по инвестициям
Рефераты по информатике
Исторические личности
Рефераты по кибернетике
Рефераты по коммуникации и связи
Рефераты по косметологии
Рефераты по криминалистике
Рефераты по криминологии
Рефераты по науке и технике
Рефераты по кулинарии
Рефераты по культурологии
Курсовая работа: Чисельні методи розв’язування крайових задач для звичайних диференціальних рівнянь
Курсовая работа: Чисельні методи розв’язування крайових задач для звичайних диференціальних рівнянь
Міністерство освіти і науки України
Сумський Державний Університет
Кафедра Інформатики
Курсова робота
на тему:
«Чисельні методи розв’язування крайових задач для звичайних диференціальних рівнянь»
«Метод скінченних різниць»
Суми 2006
Зміст
Вступ
Постановка задачі
Метод скінчених різниць
Дослідження точності
Збіжність різницевої схеми
Програмна реалізація(представлена на мові Delphi
Висновки
Література
Вступ
На сьогоднішній день існує багато чисельних методів розв’язування крайових задач для звичайних диференціальних рівнянь. Але всі вони поділяються на дві групи: наближені методи чисельного розв’язання і наближені аналітичні методи.
Наближені чисельні методи:
1.Розв'язання лінійної крайової задачі комбінуванням двох задач Коші:
Припустимо, що розв'язок задачі (11.4), (11.5) будемо шукати у вигляді
![]() (11.6)
(11.6)
де
![]() - деяка константа,
- деяка константа, ![]() - функція, що задовольняє
однорідне рівняння
- функція, що задовольняє
однорідне рівняння
![]() (11.7)
(11.7)
а
![]() - функція, яка задовольняє
неоднорідне рівняння
- функція, яка задовольняє
неоднорідне рівняння
![]() (11.8)
(11.8)
Через
те, що рівняння (11.4) є лінійним, функція ![]() буде
його розв'язком для будь-якого
буде
його розв'язком для будь-якого ![]() . Справді,
. Справді,
![]()
Якщо
припустити, що розв’язок (11.6) задовольняє першу граничну умову (11.5) для
будь-якого ![]() , то отримаємо рівняння
, то отримаємо рівняння
![]()
Ця гранична умова задовольняється, якщо покласти
![]() (11.9)
(11.9)
![]() (11.10)
(11.10)
Рівність (11.9) справедлива, коли прийняти, наприклад, що
![]() ,
, ![]() (11.11)
(11.11)
Щоб задовольнити рівність (11.10), можна покласти
![]() ,
, ![]() ,
якщо
,
якщо ![]() (11.12)
(11.12)
![]() ,
, ![]() ,
якщо
,
якщо ![]() (11.13)
(11.13)
Враховуємо,
що одночасно ![]() і
і ![]() на нуль не перетворюються
через умову (11.5).
на нуль не перетворюються
через умову (11.5).
Таким чином, для розв'язання крайової задачі (11.4), (11.5) необхідно знайти розв'язок задач
![]() ,
, ![]() ,
,
![]() (11.14)
(11.14)
![]() (11.15)
(11.15)
з
початковими умовами (11.12) чи (11 13). Для цього можна використати будь-який
чисельний метод розв'язання задачі Коші для рівнянь другого порядку. Наближений
розв'язок цих рівнянь отримуємо на відрізку ![]() ,
у результаті чого стають відомими значення
,
у результаті чого стають відомими значення ![]() ,
,![]() ,
,![]() ,
,![]() . Це дозволяє вибрати таку
константу
. Це дозволяє вибрати таку
константу ![]() . щоб функція (11.6)
задовольняла не тільки рівняння (11.12) і першу граничну умову, але і другу
граничну умову (11.5). Маємо
. щоб функція (11.6)
задовольняла не тільки рівняння (11.12) і першу граничну умову, але і другу
граничну умову (11.5). Маємо
![]() ,
,
звідки
![]() ,
,
якщо ![]() . (11.16)
. (11.16)
Коли ![]() , то однорідна крайова
задача
, то однорідна крайова
задача
![]() ,
, ![]() ,
,
![]()
мас нетривіальний
розв'язок ![]() , який є ознакою
виродженості початкової задачі (11.4), (11.5).
, який є ознакою
виродженості початкової задачі (11.4), (11.5).
2. Метод прицілювання:
Викладений вище метод редукції крайової задачі до задачі Коші має певні недоліки.
Він не дозволяє
використовувати методи розв'язання задачі Коші зі змінним порядком і змінним
кроком. Розв'язки ![]() і
і ![]() повинні обчислюватись на
сітці з однаковим кроком, інакше знайти їх комбінацію (11.6) буде неможливо.
повинні обчислюватись на
сітці з однаковим кроком, інакше знайти їх комбінацію (11.6) буде неможливо.
Використання методу, як правило, обмежується лише одновимірною лінійною задачею. Причина полягає в тому, що під час розв'язання системи рівнянь потрібно обчислювати не одне значення константи А (11.16), а матрицю А, що є далеко не простою задачею.
Метод не придатний для розв'язання нелінійних крайових задач.
Ці недоліки спричинилися до появи нових методів. На практиці двоточкова крайова задача (лінійна чи нелінійна) звичайно розв'язується методом прицілювання (стрільби), назва якого запозичена із теорії артилерійської стрільби. Відповідно до цього методу розв'язок шуканого рівняння другого порядку
![]()
із заданими граничними умовами
![]() ,
, ![]() ,
,
![]()
знаходять у такий спосіб: ітераційним розв'язанням задачі Коші
![]() (11.18)
(11.18)
![]() і
і ![]()
підбирається
значення першої похідної ![]() , для
якої виконується друга крайова умова
, для
якої виконується друга крайова умова ![]() .
.
Спочатку
вибирається довільне значення ![]() і
розв'язується задача Коші (11.18). Значення
і
розв'язується задача Коші (11.18). Значення ![]() бажано
вибирати так, щоб наближений розв'язок на кінці інтервалу задовольняв умову
бажано
вибирати так, щоб наближений розв'язок на кінці інтервалу задовольняв умову ![]() (рис 1.). Потім
вибирається
(рис 1.). Потім
вибирається ![]() , і розв'язання задачі Коші
повторюється. Тепер бажано вибрати його так, щоб виконувалась умова
, і розв'язання задачі Коші
повторюється. Тепер бажано вибрати його так, щоб виконувалась умова ![]() (рис 1.).
(рис 1.).
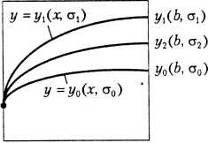
рис. 1. Ілюстрація методу стрільби.
Після цього
шляхом інтерполяції уточнюється значення ![]() для
задач Коші з початковими умовами:
для
задач Коші з початковими умовами:
![]() ,
,
![]()
…….. …….. ……..
де ![]() - наближений розв'язок
задачі Коші в точці
- наближений розв'язок
задачі Коші в точці ![]() для вибраного
значення
для вибраного
значення ![]() .
.
Метод
прицілювання є універсальним і використовується для розв'язання нелінійних
диференціальних рівнянь ![]() -ого
порядку. Слід зазначити, що довільний вибір початкового наближення
-ого
порядку. Слід зазначити, що довільний вибір початкового наближення ![]() може привести до того, що
задача (11.18) виявиться жорсткою навіть у випадку, коли задача (11.1), (11.2)
є добре обумовленою.
може привести до того, що
задача (11.18) виявиться жорсткою навіть у випадку, коли задача (11.1), (11.2)
є добре обумовленою.
Наближені аналітичні методи:
3.Метод колокацій:
У методі колокацій розв'язок крайової задачі (11.4), (11.5) шукається у вигляді функції
![]() . (11.36)
. (11.36)
де ![]() ,
, ![]() - лінійно незалежні, двічі
диференційовані базисні функції, визначені на відрізку
- лінійно незалежні, двічі
диференційовані базисні функції, визначені на відрізку![]() . Функція
. Функція ![]() повинна задовольняти
задані граничні умови (11.5):
повинна задовольняти
задані граничні умови (11.5):
![]()
![]() (11.37,а)
(11.37,а)
а функції![]() ,
, ![]() - відповідні однорідні
граничні умови, тобто
- відповідні однорідні
граничні умови, тобто
![]() ,
,
![]() ,
,
![]() . (11.37,б)
. (11.37,б)
Через лінійність
граничних умов функція ![]() у (11.36)
задовольняє граничним умовам (11.24) для будь-яких значень
у (11.36)
задовольняє граничним умовам (11.24) для будь-яких значень ![]() . Наприклад, у точці
. Наприклад, у точці ![]() маємо
маємо
![]() .
.
Аналогічно для ![]() отримаємо
отримаємо
![]()
Суть методу
колокацій полягає в тому, що для заданих ![]() точок
на відрізку
точок
на відрізку ![]() , названих вузлами
колокації, підбирають значення
, названих вузлами
колокації, підбирають значення ![]() так,
щоб отримана при цьому функція
так,
щоб отримана при цьому функція ![]() (11.36)
задовольняла рівняння (11.4) у кожному з вузлів колокації:
(11.36)
задовольняла рівняння (11.4) у кожному з вузлів колокації:
![]() ,
,![]() (11.38)
(11.38)
де
![]() ,
, ![]() .
.
Покладемо
![]() , (11.39)
, (11.39)
![]()
тоді (11.39) матиме стандартний вигляд системи лінійних алгебраїчних рівнянь:
![]() ,
, ![]() (11.40)
(11.40)
відносно
коефіцієнтів ![]() . Якщо розв'язати цю
систему і підставити отримані значення коефіцієнтів у вираз (11.36), отримаємо
наближений розв'язок
. Якщо розв'язати цю
систему і підставити отримані значення коефіцієнтів у вираз (11.36), отримаємо
наближений розв'язок ![]() .
.
Точність
розв'язку крайової задачі методом колокацій залежить від типу базисних функцій ![]() . У конкретних задачах
вибір цих функцій слід здійснювати з урахуванням апріорної інформації про
розв'язки задачі або на основі емпіричних даних. Нехай
. У конкретних задачах
вибір цих функцій слід здійснювати з урахуванням апріорної інформації про
розв'язки задачі або на основі емпіричних даних. Нехай ![]() - це лінійна функція
- це лінійна функція
![]() , (11.41)
, (11.41)
параметри якої визначимо таким чином, щоб вона задовольняла неоднорідні граничні умови (11.5), тобто з системи рівнянь
![]() ,
,
![]() . (11.42)
. (11.42)
Функції ![]() можна задати у вигляді:
можна задати у вигляді:
![]() ,
, ![]() . (11.43)
. (11.43)
Очевидно, що за
будь-яких ![]() функція (11.43)
задовольняє умову (11.37, а). Значення
функція (11.43)
задовольняє умову (11.37, а). Значення ![]() ,
за якого буде задовольнятися друга умова (11.37, б), таке:
,
за якого буде задовольнятися друга умова (11.37, б), таке:
![]() . (11.44)
. (11.44)
Якщо в умовах
(11.37, а, б) ![]() , то можливий
інший вибір, а саме:
, то можливий
інший вибір, а саме:
![]() ,
,
![]() . (11.45)
. (11.45)
4.Метод Гальоркіна
Як і в методі колокацій, у методі Гальоркіна наближений розв'язок крайової задачі (11.4), (11.5) шукаємо у вигляді
![]() (11.48)
(11.48)
де ![]() ,
, ![]() - лінійно незалежні, двічі
диференційовані базисні функції, визначені на відрізку
- лінійно незалежні, двічі
диференційовані базисні функції, визначені на відрізку ![]() . Функція
. Функція ![]() повинна задовольняти
задані граничні умови (11.37, а), а функції
повинна задовольняти
задані граничні умови (11.37, а), а функції ![]() ,
,
![]() - відповідні однорідні
граничні умови (11.37, 6).
- відповідні однорідні
граничні умови (11.37, 6).
Необхідно, щоб
система базисних функцій ![]() ,
, ![]() була ортогональною на
відрізку
була ортогональною на
відрізку ![]() , тобто
, тобто
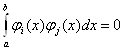 при
при ![]() і
і
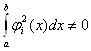 ,
,
і повною. Остання
вимога означає, що не повинно існувати ніякої іншої відмінної від нуля функції,
яка ортогональна до всіх функцій ![]() ,
, ![]() .
.
Використовуючи наближений розв'язок (11.48) знайдемо нев'язку:
![]() (11.49)
(11.49)
Коефіцієнти ![]() мають бути такими, щоб
значення інтеграла від квадрата нев'язки
мають бути такими, щоб
значення інтеграла від квадрата нев'язки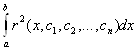
було найменшим.
Це досягається
лише в тому випадку, коли нев'язка ![]() ортогональна
до всіх базисних функцій
ортогональна
до всіх базисних функцій ![]() . Умову
ортогональності запишемо у вигляді:
. Умову
ортогональності запишемо у вигляді:
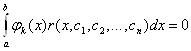 ,
, ![]()
або
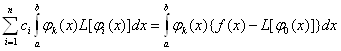 ,
, ![]() (11.50)
(11.50)
Таким чином,
отримаємо систему лінійних алгебраїчних рівнянь для обчислення коефіцієнтів ![]()
5.Метод найменших квадратів
У методі найменших квадратів наближений розв'язок крайової задачі (11.4) і (11.5) задасться у вигляді:
![]() , (11.54)
, (11.54)
де ![]() ,
, ![]() - лінійно незалежні, двічі
диференційовані базисні функції, визначені на відрізку
- лінійно незалежні, двічі
диференційовані базисні функції, визначені на відрізку ![]() . Функція
. Функція ![]() повинна задовольняти
задані граничні умови (11.37, а), а функції
повинна задовольняти
задані граничні умови (11.37, а), а функції ![]() ,
,
![]() - відповідні однорідні
граничні умови (11.38, б).
- відповідні однорідні
граничні умови (11.38, б).
Підставимо наближений розв'язок (11.54) у рівняння (11.4) і знайдемо нев'язку:
![]() , (11.55)
, (11.55)
абсолютна
величина якої для ![]() повинна бути
якомога меншою. Тому вимагатимемо, щоб виконувалася умова
повинна бути
якомога меншою. Тому вимагатимемо, щоб виконувалася умова
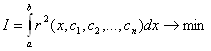 (11.56)
(11.56)
Значення інтегралу будуть мінімальними за умов:
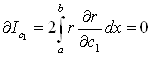 ,
,
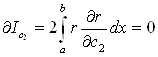 ,
,
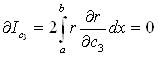 ,
,
… … … …
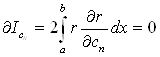 .
.
На основі цих
умов формується система лінійних рівнянь для обчислення коефіцієнтів ![]() .
.
6.Метод скінченних елементів
Метод Гальоркіна
накладає певні обмеження на вибір системи базисних функцій, які залежать від
граничних умов крайової задачі. Це обмеження значно ускладнює реалізацію методу,
особливо під час розв'язання задач математичної фізики. Це обмеження можна
подолати, якщо для апроксимації розв'язку використовувати систему простих
базисних функцій, які залежать від координат вузлів на відрізку ![]() . У цьому випадку
розв'язання крайової задачі зводиться до формування і розв'язання системи
лінійних алгебраїчних рівнянь, тому метод отримав назву методу скінченних
елементів. Його часто використовують для розв'язання дво- та тривимірних
диференціальних рівнянь із частинними похідними.
. У цьому випадку
розв'язання крайової задачі зводиться до формування і розв'язання системи
лінійних алгебраїчних рівнянь, тому метод отримав назву методу скінченних
елементів. Його часто використовують для розв'язання дво- та тривимірних
диференціальних рівнянь із частинними похідними.
Шукатимемо наближений розв'язок задачі
![]() ,
, ![]() (11.59)
(11.59)
як лінійну комбінацію простих однотипних функцій
![]() , (11.60)
, (11.60)
що мають вигляд
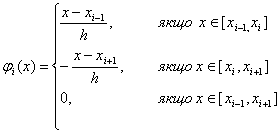 (11.61)
(11.61)
і, як правило,
називаються фінітними. Графік однієї з таких функцій наведено на рис. 2, де
видно, що функція не дорівнює нулю тільки на інтервалі ![]() . Щодо множини фінітних
функцій, які задаються на відрізку
. Щодо множини фінітних
функцій, які задаються на відрізку ![]() відомо,
що вони лінійно незалежні (більш того, ортогональні в спеціальній енергетичній
нормі) і утворюють повну систему в просторі
відомо,
що вони лінійно незалежні (більш того, ортогональні в спеціальній енергетичній
нормі) і утворюють повну систему в просторі ![]() .Це
дає підставу використати їх як базисні функції в методі Гальоркіна.
.Це
дає підставу використати їх як базисні функції в методі Гальоркіна.
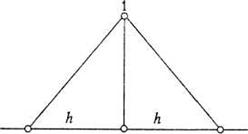
рис. 2. Графік фінітної функції.
Запишемо умову ортогональності (11.50):
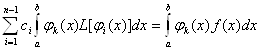 ,
, ![]() (11.62)
(11.62)
і отримаємо
систему лінійних алгебраїчних рівнянь для знаходження невідомих ![]() .Праві частини цих рівнянь
позначимо через
.Праві частини цих рівнянь
позначимо через ![]() і отримаємо для
їх обчислення вираз
і отримаємо для
їх обчислення вираз
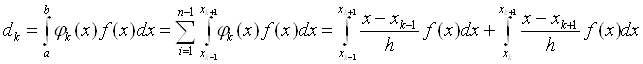 (11.63)
(11.63)
Коефіцієнти системи рівнянь (11.62) позначимо через
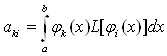
Знайдемо вирази
для коефіцієнтів системи рівнянь ![]() з
невідомими
з
невідомими ![]() . Підставляючи в останній
вираз
. Підставляючи в останній
вираз ![]() , отримаємо
, отримаємо
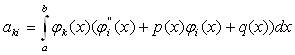
Перший з інтегралів у цьому виразі обчислимо по частинах:
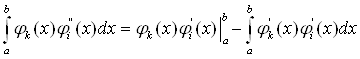
Оскільки за
граничних умов (11.60) використовуються ![]() ,
базисних функцій від
,
базисних функцій від ![]() до
до ![]() і всі вони в точках
і всі вони в точках ![]() і
і ![]() дорівнюють 0, то
дорівнюють 0, то
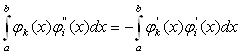
Тоді вираз для обчислення набуває вигляду:
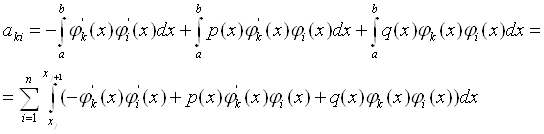 (11.64)
(11.64)
Для обчислення ![]() треба знайти значення
похідних від фінітних функцій. Із цією метою диференціюємо (11.61) і отримуємо:
треба знайти значення
похідних від фінітних функцій. Із цією метою диференціюємо (11.61) і отримуємо:
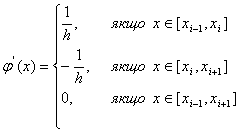 (11.65)
(11.65)
Функція відмінна
від нуля тільки на інтервалі ![]() . Крім
того, на одному і тому ж інтервалі ненульовими є дві базисні функції і їх
похідні з сусідніми індексами (рис. 3), тобто на інтервалі
. Крім
того, на одному і тому ж інтервалі ненульовими є дві базисні функції і їх
похідні з сусідніми індексами (рис. 3), тобто на інтервалі ![]() відмінні від нуля
відмінні від нуля ![]() ,
, ![]() ,
, ![]() ,
, ![]() і т. д.
і т. д.
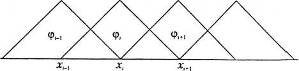
рис. 3. Система фінітних функцій.
У виразі для ![]() (11.64) добутки
(11.64) добутки ![]() ,
, ![]() ,
, ![]() можна вважати відмінними
від нуля тому, що на елементарному інтервалі не дорівнюють нулю фінітні функції
та їх похідні, які мають сусідні індекси у випадках, коли
можна вважати відмінними
від нуля тому, що на елементарному інтервалі не дорівнюють нулю фінітні функції
та їх похідні, які мають сусідні індекси у випадках, коли ![]() . А це означає, що
. А це означає, що
![]() для
для ![]() , (11.66)
, (11.66)
тобто матриця
системи ![]() (11.62) є тридіагональною
матрицею. її ненульові елементи обчислюються таким чином. Формули для
діагональних елементів отримаємо, приймаючи
(11.62) є тридіагональною
матрицею. її ненульові елементи обчислюються таким чином. Формули для
діагональних елементів отримаємо, приймаючи ![]() у
виразі (11.64):
у
виразі (11.64):
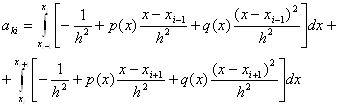 (11.67)
(11.67)
Для ![]() , отримаємо формули для
елементів правої бічної діагоналі матриці
, отримаємо формули для
елементів правої бічної діагоналі матриці ![]() :
:
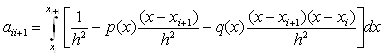 , (11.68)
, (11.68)
а для ![]() - лівої;
- лівої;
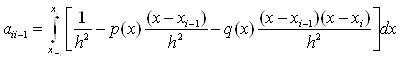
Три останні
вирази визначають систему алгебраїчних рівнянь (11.62) для невідомих
коефіцієнтів ![]() .
.
Розглянемо розв’язання задачі (11.59) у випадку неоднорідних граничних умов
![]() ,
, ![]() (11.70)
(11.70)
і зведемо її до розв'язання задачі з однорідними граничними умовами. Для цього введемо заміну:
![]() , де
, де ![]() .
.
Двічі диференціюючи цю функцію і підставляючи вирази для похідних у рівняння (11.59), отримаємо крайову задачу з однорідними граничними умовами:
![]() ,
,
![]() ,
, ![]() . (11.71)
. (11.71)
Постановка задачі
Щоб знайти єдиний розв'язок звичайного диференціального рівняння, необхідно задати деякі допоміжні умови, що використовуються для обчислення інтегрування. Для рівняння n-ого порядку потрібно п таких умов. Якщо ці умови задаються для одного значення незалежної змінної (зокрема, для одного кінця інтервалу, на якому необхідно знайти розв'язок), то говорять про початкові умови для задачі Коші. Якщо ж додаткові умови задаються для значень незалежної змінної на різних кінцях інтервалу, то мають на увазі крайову задачу і граничні умови для неї.
Двоточкова крайова задача для рівняння другого порядку має такий вигляд:
![]()
![]() (11.1)
(11.1)
із граничними умовами
![]() (11.2)
(11.2)
Перш ніж застосовувати будь-який чисельний метод, варто перевірити умови, що гарантують існування розв'язку цієї задачі. Наведена нижче теорема визначає загальні умови, що забезпечують існування й одиничність розв'язку.
Теорема. Припустимо,
що ![]() неперервна в області
неперервна в області
![]()
І що
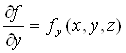 і
і 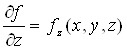
Теж
неперервні на![]() . Якщо існує постійна
. Якщо існує постійна![]() , для якої виконуються
умови
, для якої виконуються
умови
![]() для всіх
для всіх ![]()
![]() для всіх
для всіх ![]() (11.3)
(11.3)
то
крайова задача (11.1) (11.2) має єдиний розв'язок ![]() для
для
![]() .
.
Найчастіше зустрічаються і найкраще вивчені двоточкові лінійні крайові задачі виду
![]() ,
, ![]() (11.4)
(11.4)
![]() ,
, ![]() (11.5)
(11.5)
де
![]() ,
, ![]()
Умови,
які повинні задовольняти функції ![]() ,
, ![]() і
і ![]() , для того щоб задача
(11.4), (11.5) мала єдиний розв'язок, випливають із теореми як наслідок.
, для того щоб задача
(11.4), (11.5) мала єдиний розв'язок, випливають із теореми як наслідок.
Наслідок. Якщо ![]() і
і ![]() неперервні на
неперервні на ![]() і
і ![]() , то задача (11.4), (11.5)
має єдиний розв'язок на
, то задача (11.4), (11.5)
має єдиний розв'язок на ![]() .
.
Граничні
умови (11.5) визначають третю крайову задачу для рівняння (11.4). Якщо
припустити, що ![]() , то умови (11.5)
визначають першу крайову задачу, а коли
, то умови (11.5)
визначають першу крайову задачу, а коли ![]() -
другу.
-
другу.
Точне
(аналітичне) розв'язання крайових задач - більш складна процедура, ніж
знаходження розв'язку задачі Коші. Це спричинило появу великої кількості
наближених методів. Ці методи можна розділити на дві групи:
наближено-аналітичні методи, що дають наближений розв'язок крайової задачі на
відрізку ![]() у вигляді конкретної
аналітичної функції, і чисельні методи, що визначають розвозок у вигляді
табличної функції, заданої на сітці відрізка
у вигляді конкретної
аналітичної функції, і чисельні методи, що визначають розвозок у вигляді
табличної функції, заданої на сітці відрізка ![]() .
.
Метод скінченних різниць
Ідея методу
скінченних різниць полягає в тому, що похідні в диференціальному рівнянні
(11.4) і граничних умовах (11.5) заміняються їх скінченними різницями. Для
цього спочатку введемо на відрізку ![]() сітку з
кроком
сітку з
кроком ![]() :
:
![]() .
.
Позначимо через ![]() точний розв'язок задачі
(11.1) у і-му вузлі сітки, а через
точний розв'язок задачі
(11.1) у і-му вузлі сітки, а через ![]() -
наближений розв'язок у цій точці. Заміняючи в кожному внутрішньому вузлі сітки
похідні різницями, отримаємо різницеві рівняння:
-
наближений розв'язок у цій точці. Заміняючи в кожному внутрішньому вузлі сітки
похідні різницями, отримаємо різницеві рівняння:
![]() ,
, ![]()
Симетричні
різницеві апроксимації похідних першого і другого порядків мають похибку
другого порядку відносно ![]() , тобто
, тобто ![]() . Це легко довести на
основі розкладання в ряд Тейлора точного розв'язку рівняння. Дійсно, для вузлів
. Це легко довести на
основі розкладання в ряд Тейлора точного розв'язку рівняння. Дійсно, для вузлів
![]() та
та ![]() маємо
маємо
![]()
![]()
з різниці яких отримуємо шуканий результат:
![]() ,
,
![]() (11.21)
(11.21)
Знайдемо нев’язку різницевого рівняння
![]() .
.
Оскільки ![]() є точним розв'язком
рівняння (11.4),
є точним розв'язком
рівняння (11.4),
![]() та
та ![]() . (11.22)
. (11.22)
Тому різницеве рівняння (11.21) апроксимує вихідне диференціальне рівняння
(11.4) також із
другим порядком відносно ![]() .
.
Тепер апроксимуємо граничні умови скінченними різницями:
![]() ,
, ![]() (11.23)
(11.23)
Знайдемо похибку апроксимації граничних умов. Нев’язки граничних умов (11.23) мають вигляд:
![]() ,
, ![]() .
.
Асиметрична
апроксимація першої похідної на відміну від симетричної має глобальну похибку
першого порядку відносно ![]() , тобто
, тобто ![]() . Це безпосередньо випливає
з розкладання в ряд Тейлора
. Це безпосередньо випливає
з розкладання в ряд Тейлора
![]() ,
,
із якого отримуємо
![]() ,
, ![]()
Отже, граничні умови (11.23) апроксимуються з першим порядком за к. Порядок їх апроксимації можна підвищити до другого, наприклад, використовуючи співвідношення
![]()
![]() ,
,![]() (11.24)
(11.24)
похибка
апроксимації яких також пропорційна ![]() , як і
для випадку симетричної апроксимації похідних. Це випливає із порівняння двох
рядів Тейлора:
, як і
для випадку симетричної апроксимації похідних. Це випливає із порівняння двох
рядів Тейлора:
![]()
![]()
Якщо перший вираз помножити на 4 і відняти його від другого, отримаємо:
![]() .
.
Після його підстановки у формулу (11.24) знаходимо нев'язку у вигляді:
![]()
тобто крайова
умова апроксимується з другим порядком відносно ![]() .
.
У такий же спосіб
доводиться, що і друга гранична умова (11.23) апроксимується з другим порядком
відносно ![]() .
.
Розглянемо ще одну можливість апроксимації крайових умов типу (11.5) на прикладі умови
![]() .
.
Для цього за
межами інтервалу ![]() вводиться
додаткова точка
вводиться
додаткова точка ![]() , за допомогою
якої обчислюється перша похідна за симетричною формулою апроксимації:
, за допомогою
якої обчислюється перша похідна за симетричною формулою апроксимації:
![]() . (11.25)
. (11.25)
Точку ![]() можна виключити,
скориставшись співвідношенням (11.25) і різницевою апроксимацією
диференціального рівняння (11.4) в кінцевій точці інтервалу
можна виключити,
скориставшись співвідношенням (11.25) і різницевою апроксимацією
диференціального рівняння (11.4) в кінцевій точці інтервалу ![]() .
.
Отримуємо
рівняння для граничної умови в точці ![]() із
порядком
із
порядком ![]() , яким можна замінити
останнє рівняння в системі алгебраїчних рівнянь, одержаній у разі
кусочно-різницевої апроксимації похідних у рівнянні (11.4).
, яким можна замінити
останнє рівняння в системі алгебраїчних рівнянь, одержаній у разі
кусочно-різницевої апроксимації похідних у рівнянні (11.4).
Те ж саме можна
зробити з першою умовою (11.5) і першим апроксимуючим рівнянням для ![]() . Варто підкреслити, що
врахування граничних умов різних типів впливає тільки на перше й останнє
рівняння цієї системи.
. Варто підкреслити, що
врахування граничних умов різних типів впливає тільки на перше й останнє
рівняння цієї системи.
Зведемо подібні члени в рівнянні (11.21) і отримаємо стандартне триточкове різницеве рівняння:
![]() , (11.27)
, (11.27)
![]() .
.
Включивши до
системи рівнянь (11.25) різницеве рівняння (11.23) чи (11.24), отримаємо
систему рівнянь, що містить ![]() рівняння
з
рівняння
з ![]() невідомими
невідомими ![]() .
.
Порівняємо ці два
варіанти апроксимації крайової задачі. У першому з них система лінійних
алгебраїчних рівнянь, утворена рівняннями (11.21) і (11.23), має тридіагональну
матрицю коефіцієнтів, і її можна розв'язати методом прогону. Щоб застосувати
метод прогону в другому випадку, слід створити відповідну тридіагональну
матрицю. Для цього потрібно з першого рівняння (11.27) для ![]()
![]()
Маємо рівняння з
двома невідомими - ![]() і
і ![]() . Замінимо ним перше
рівняння (11.24). Виконаємо такі ж перетворення з другим (11.24) і останнім
рівнянням (11.27) для
. Замінимо ним перше
рівняння (11.24). Виконаємо такі ж перетворення з другим (11.24) і останнім
рівнянням (11.27) для ![]() :
:
![]()
Виключивши з них ![]() , знаходимо:
, знаходимо:
![]()
Це рівняння
містить дві невідомі - ![]() і
і ![]() . Замінимо ним друге
рівняння (11.27). Два останні рівняння разом із (11.27) утворюють систему
рівнянь із тридіагональною матрицею, що апроксимує вихідну крайову задачу
(11.4), (11.5) з порядком
. Замінимо ним друге
рівняння (11.27). Два останні рівняння разом із (11.27) утворюють систему
рівнянь із тридіагональною матрицею, що апроксимує вихідну крайову задачу
(11.4), (11.5) з порядком ![]() . Цю
систему також можна розв'язати методом прогону. Метод прогону є стійким, якщо
матриця коефіцієнтів діагонально домінантна. Забезпечити діагональну
домінантність можна обранням кроку
. Цю
систему також можна розв'язати методом прогону. Метод прогону є стійким, якщо
матриця коефіцієнтів діагонально домінантна. Забезпечити діагональну
домінантність можна обранням кроку ![]() . Для
цього необхідно, щоб для системи рівнянь (11.27) виконувались умови:
. Для
цього необхідно, щоб для системи рівнянь (11.27) виконувались умови:
![]() і
і ![]() ,
, ![]() .
.
Підсилюючи останні нерівності, маємо такі обмеження на величину кроку:
![]() і
і ![]() ,
, ![]() . (11.28)
. (11.28)
Щоб задовольнялись умови (11.23), мають виконуватись нерівності
![]() і
і ![]() . (11.29)
. (11.29)
Наявність обмежень (11.28) і (11.29) свідчить про умовну стійкість розглянутого методу апроксимації.
Дослідження точності
Дослідження точності отриманих виразів при чисельних розрахунках зручно робити за допомогою апостеріорної оцінки, по швидкості спадання членів відповідного ряду Тейлора. Якщо крок сітки досить малий, то похибка близька до першого відкинутого члена.
У такий спосіб порядок точності результату стосовно кроку сітки дорівнює числу залишених членів ряду, чи іншими словами, він дорівнює числу вузлів інтерполяції мінус порядок похідної. тому мінімальне число вузлів необхідне для обчислення m-ої похідної, дорівнює m+1, воно забезпечує перший порядок точності.
Ці висновки відповідають принципу: при почленному диференціюванні ряду швидкість його збіжності зменшується.
Якщо врахувати погіршення збіжності ряду при диференціюванні, то можна зробити висновок: навіть якщо функція задана добре складеною таблицею на досить докладній сітці, то практично чисельним диференціюванням можна визначити першу і другу похідні, а третю і четверту – лише з великою похибкою. Похідні більш високого порядку рідко вдається обчислити з задовільною точністю.
Одним з найбільш простих і досить ефективних методів оцінки похибки й уточнення отриманих результатів є правило Рунге. Для оцінки похибки за правилом Рунге порівнюють наближені розв’язки, отримані при різних кроках сітки. При цьому використовується наступне припущення: глобальна похибка методу порядку p у точці хi подається у вигляді
![]()
![]() .
.
За формулою Рунге
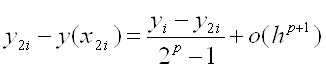
Таким чином, із
точністю до ![]() (величина більш високого
порядку малості) при h→0 похибка методу має вигляд:
(величина більш високого
порядку малості) при h→0 похибка методу має вигляд:
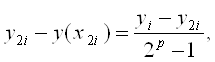
де yi
– наближене значення, отримане в точці ![]() з
кроком h; y2i – із кроком h/2; p
- порядок методу; y(x2i) - точний розв’язок задачі.
з
кроком h; y2i – із кроком h/2; p
- порядок методу; y(x2i) - точний розв’язок задачі.
Формула Рунге:
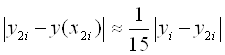 .
.
Збіжність різницевої схеми
Постановка задачі
Універсальним
методом наближеного розв’язання, є метод скінченних різниць. Як задачі
представлені у вигляді систем нелінійних рівнянь у часткових, які розглядаються
у області ![]()
Розв’язок
задачі в ![]() має додаткові умови:
має додаткові умови:
1) умови при ![]() називають початковими
умовами;
називають початковими
умовами;
2) умови на границі ![]() області
області ![]() — крайовими
або граничними умовами.
— крайовими
або граничними умовами.
Задача з початковими умовами – називається задачею Коші.
Нехай
![]() . Тоді для функції
. Тоді для функції ![]() маємо задачу:
маємо задачу:
![]() (1)
(1)
![]() (2)
(2)
де
![]() и
и![]() - диференціальні
оператори задачі і крайових умов. Припустимо ,що відповідно задачі (1-2)
поставлені коректно, тобто оператори А и R; область D и її
границі Г такі, що при виборі відповідних класів функцій і правих частин у
рівняннях (1) и (2) розв’язок існує, і залежить від початкових даних.
- диференціальні
оператори задачі і крайових умов. Припустимо ,що відповідно задачі (1-2)
поставлені коректно, тобто оператори А и R; область D и її
границі Г такі, що при виборі відповідних класів функцій і правих частин у
рівняннях (1) и (2) розв’язок існує, і залежить від початкових даних.
Різницева схема
Введемо
у області ![]() сітку
сітку ![]() , яка складається з множини
внутрішніх вузлів
, яка складається з множини
внутрішніх вузлів ![]() і множини
граничних вузлів
і множини
граничних вузлів ![]() :
:
Далі
розглянемо сіткові функції ![]() і з їх
допомогою побудуємо наближений розв’язок задачі (1-2). Для цього відносно
і з їх
допомогою побудуємо наближений розв’язок задачі (1-2). Для цього відносно ![]() сформулюємо
"різницеву задачу", заміняючи оператори задачі
сформулюємо
"різницеву задачу", заміняючи оператори задачі ![]() і
і ![]() і їх сітковим аналогами
і їх сітковим аналогами ![]() и
и![]() . Тоді на сітковому
шаблоні
. Тоді на сітковому
шаблоні ![]() маємо
маємо
![]() (3)
(3)
![]() (4)
(4)
Задачу
(3)-(4) назвемо різницевою схемою для задачі (1)-(2). Звичайно це алгебраїчна
система рівнянь відносно ![]() .
.
При переході від початкової задачі (1)-(2) до її різницевого аналогу (3)-(4) особливо важливі 3 групи питань:
-
існування, єдиність і алгоритм побудови різницевого розв’язку ![]() ;
;
-
при яких умовах різницевий розв’язок ![]() збігається
до точного розв’язку
збігається
до точного розв’язку ![]() і яка при
цьому швидкість збіжності;
і яка при
цьому швидкість збіжності;
-
як конкретно вибирати сітку ![]() і
побудувати різницеву схему
і
побудувати різницеву схему ![]() і
і ![]() у задачі (3)-(4).
у задачі (3)-(4).
Нев’язка різницевої схеми
При побудові різницевого рівняння задачі
![]()
ми
отримали задачу, якої точний розв’язок ![]() ,
як правило, не задовольняє. Сіткову функцію
,
як правило, не задовольняє. Сіткову функцію
![]()
називають нев’язкою сіткового рівняння (3). Її зручно представити на розв’язку и(х) у вигляді:
![]() на
на ![]() (5)
(5)
Аналогічно знаходяться нев’язки граничних умов
![]() на
на ![]() (5')
(5')
Як
правило нев’язки ![]() і
і ![]() оцінюють по
параметру
оцінюють по
параметру ![]() через розклад у ряд
Тейлора в припущені гладкості відповідного розв’язку
через розклад у ряд
Тейлора в припущені гладкості відповідного розв’язку ![]() для отримання
представлення нев’язки з залишковим членом виду
для отримання
представлення нев’язки з залишковим членом виду ![]() .
.
Апроксимація різницевої схеми
Різницева схема (3)-(4) апроксимує задачу (1)-(2), якщо має місце:
![]()
![]() (6)
(6)
Тобто
відповідні нев’язки ![]() 0 к нулю при
0 к нулю при ![]() .
.
Апроксимація задачі (1)-(2) має порядок![]() ,
якщо
,
якщо
![]() (6')
(6')
У
цих випадках норми рахуються для сіткових функцій на ![]() і
і ![]() але у своїх функціональних
просторах.
але у своїх функціональних
просторах.
Зауваження:
Сам
розв’язок задачі (1)-(2) ,як правило невідомий і використовувати його для
отримання нев’язок ![]() і
і ![]() не можна. Тому
беруть широкий клас функцій
не можна. Тому
беруть широкий клас функцій ![]() і
вимагають апроксимації порядку к задачі (1)-(2)
і
вимагають апроксимації порядку к задачі (1)-(2) ![]()
![]() , тобто
, тобто
![]() .
.
При
цьому на розв’язку ![]() задачі
(1)-(2) апроксимація буде не гірше, ніж порядок
задачі
(1)-(2) апроксимація буде не гірше, ніж порядок ![]()
Як правило схема (3)-(4) по різним змінним має різний порядок апроксимації , наприклад, нев’язка рівняння
![]()
Така апроксимація називається абсолютною на відміну від умовної апроксимації у випадку, коли, наприклад
![]()
При умовній апроксимації різницеве рівняння може апроксимувати різні диференціальні задачі.
Стійкість різницевої схеми
Відсутність
стійкості різницевої схеми характеризується тим, що малі помилки, допущені на
якому-небудь етапі обчислення, надалі сильно зростають і роблять непридатним
результат розрахунку (чи взагалі неможливим сам розрахунок). Звичайно стійкість
різницевої схеми оцінюють по погрішності вхідних даних, оскільки погрішність
апроксимації, у силу визначення (6), при ![]()
![]() до нуля. Виділимо в
структурі погрішності ці доданки:
до нуля. Виділимо в
структурі погрішності ці доданки:
![]()
Типовий графік залежності погрішності сіткового рішення від величини кроку такий:
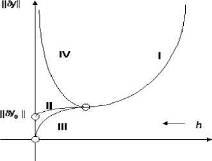
I - При зменшенні кроку спочатку погрішність усіх схем убуває, тому що істотно зменшується погрішність апроксимації.
П -
Для стійких схем погрішність сіткового рішення буде прагнути до скінченої
величини, зв'язаної з помилкою вхідних даних. Якщо при ![]() помилка вхідних даних
зникає, те - це випадок III. Тобто стійка схема в цьому випадку дозволяє
одержати як завгодно високу точність розрахунку.
помилка вхідних даних
зникає, те - це випадок III. Тобто стійка схема в цьому випадку дозволяє
одержати як завгодно високу точність розрахунку.
Якщо
ж схема не стійка (IV), то при ![]() похибка
похибка
![]() зростає(чи зростає об’єм
не стійких обчислень). Похибка
зростає(чи зростає об’єм
не стійких обчислень). Похибка ![]() буде
мати ненульовий мінімум і вже неможливо одержати як завгодно високу точність
розрахунку.
буде
мати ненульовий мінімум і вже неможливо одержати як завгодно високу точність
розрахунку.
Як
правило похибка вхідних даних і апроксимації мають степеневий
характер залежності від ![]() ; а не
стійкість приводить до зростання похибки розв’язку по експоненціальному закону
; а не
стійкість приводить до зростання похибки розв’язку по експоненціальному закону ![]() і при
і при ![]() розрахунки втрачають сенс.
Нагадаємо
розрахунки втрачають сенс.
Нагадаємо
Різницева схема (3-4)стійка по вхідним даним ![]() і
і
![]() , якщо розв’язок різницевої
схеми неперервно залежить від вхідних даних і ця залежність рівномірна відносно
кроку сітки
, якщо розв’язок різницевої
схеми неперервно залежить від вхідних даних і ця залежність рівномірна відносно
кроку сітки ![]() , тобто є
, тобто є ![]() (
(![]() не залежить від
не залежить від ![]() ) таке, що
) таке, що
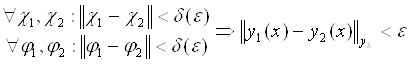 (7)
(7)
Для
лінійних схем різницеве рішення лінійно залежить від вхідних даних (у силу
лінійності зворотного оператора)і ![]() . Тоді
. Тоді
![]()
Зауваження:
На стійкість різницевої схеми впливає не тільки апроксимація рівнянь (1) (тобто оператора А), але, і особливо, крайових умов (2).
Якщо змінних у задачі мало, то розглядають безумовну й умовну стійкість;
Збіжність різницевої схеми
Розв’язуючи сіткову задачу (3)-(4) нас цікавить близькість сіткового розв’язку у(х) до розв’язку и(х) задачі (1)-(2). Різницевий розв’язок у(х) збігається до розв’язку и(х), якщо
![]() (10)
(10)
Різницевий розв’язок має порядок точності ![]() ,
якщо
,
якщо
![]() (10')
(10')
Нагадаємо
ще раз, що ми розглядаємо лише коректні різницеві схеми (3)-(4), тобто рішення
різницевої схеми існує і єдино при будь-яких вхідних даних ![]() и
и ![]() з заданих класів функцій і
схема стійка по вхідним даної (її рішення неперервно них залежить).
з заданих класів функцій і
схема стійка по вхідним даної (її рішення неперервно них залежить).
Теорема: Якщо розв’язок задачі (1)-(2) ![]() існує,
різницева схема (3)-(4) коректна и апроксимує задачу (1)-(2), то різницевий
розв’язок
існує,
різницева схема (3)-(4) коректна и апроксимує задачу (1)-(2), то різницевий
розв’язок ![]() збігається до точного:
збігається до точного:
![]()
("Апроксимація + Стійкість =>Збіжність").
Доведення: Запишемо нев’язку різницевої схеми (3)-(4).
![]() (*)
(*)
Функція
u(x) задовольняє задачі (*) — збуреній задачі (3)-(4). Так як схема
стійка, то ![]() :
:
![]()
В
силу апроксимації ![]() має місце
має місце
![]()
Таким
чином: ![]() маємо
маємо
![]()
тобто
![]() і при
і при ![]()
Зауваження:
Якщо яка-небудь дана нам умова апроксимується точно, то стійкість по ній можна не вимагати, тому що вона не вносить похибки у розв’язок (окрім помилок округлення, тоді стійкість по цим даним потрібна).
Для умовної апроксимації (чи стійкості) збіжність теж носить умовний характер.
Програмна реалізація(представлена на мові Delphi)
Розв’язати диференційне рівняння:
![]()
З крайовими умовами:
![]()
![]()
Розв’язання з використанням методу Гауса:
unit Unit1;
interface
uses
Windows, Messages, SysUtils, Variants, Classes, Graphics, Controls, Forms,
Dialogs, ExtCtrls, StdCtrls, Buttons;
type
TForm1 = class(TForm)
Panel1: TPanel;
Label1: TLabel;
Image1: TImage;
Image2: TImage;
Label2: TLabel;
LabeledEdit1: TLabeledEdit;
LabeledEdit2: TLabeledEdit;
LabeledEdit3: TLabeledEdit;
LabeledEdit4: TLabeledEdit;
LabeledEdit5: TLabeledEdit;
LabeledEdit6: TLabeledEdit;
LabeledEdit7: TLabeledEdit;
LabeledEdit8: TLabeledEdit;
LabeledEdit9: TLabeledEdit;
LabeledEdit10: TLabeledEdit;
LabeledEdit11: TLabeledEdit;
Label3: TLabel;
Label4: TLabel;
SpeedButton1: TSpeedButton;
LabeledEdit12: TLabeledEdit;
Label5: TLabel;
Image3: TImage;
procedure FormCreate(Sender: TObject);
procedure SpeedButton1Click(Sender: TObject);
private
{ Private declarations }
public
{ Public declarations }
end;
var
Form1: TForm1;
type Dynmas=array of array of real;
dynvec=array of real;
var a,b,pi,qi,fi,a1,a2,b1,b2,AA,BB:real;
eps,h:real;
c:dynmas;
st,m,i:integer;
x,d,y,memory:dynvec;
t_all,tx,ty,k_i:textfile;
g:boolean;
str:string;
implementation
uses Unit2;
{$R *.dfm}
function Gauss(n:Integer; a:dynmas; b:dynVec; var x:dynVec):Boolean;
Var i,j,k,l:Integer;
q,m,t:real;
Begin
for k:=0 to n-2 do
begin
l:=-1;
m:=0;
for i:=k to n-1 do
if Abs(a[i, k])>m then
begin
m:=Abs(a[i, k]);
l:=i;
end;
if l=-1 then
begin
Gauss:=false;
Exit;
end;
if l<>k then
begin
For j:=0 to n-1 do
begin
t:=a[k,j];
a[k,j]:=a[l,j];
a[l,j]:=t;
end;
t:=b[k];
b[k]:=b[l];
b[l]:=t;
end;
for i:=k+1 to n-1 do
begin
q:=a[i,k]/a[k,k];
for j:=0 to n-1 do
If j=k then
a[i,j]:= 0
else
a[i,j]:= a[i,j]-q*a[k,j];
b[i]:=b[i]-q*b[k];
end;
end;
if a[n-1,n-1]<>0 then
x[n-1]:=b[n-1]/a[n-1,n-1]
else
begin
Gauss:=false;
Exit;
end;
for i:=n-2 downto 0 do
begin
t:=0;
for j:=1 to n-i do
t:=t+a[i,i+j]*x[i+j];
x[i]:=(1/a[i,i])*(b[i]-t);
end;
Gauss := true;
end;
procedure Koef(var s:dynmas; k:integer; h:real; v:dynvec; var z:dynvec);
var i:integer;
begin
s[0,0]:=h*a1-a2; s[0,1]:=a2;
z[0]:=h*AA;
for i:=0 to 2*(k-1) do
begin
s[i+1,i]:=1-(h*pi*ln(v[i]))/2;
s[i+1,i+1]:=h*h*qi-2;
s[i+1,i+2]:=1+(h*pi*ln(v[i]))/2;
z[i+1]:=h*h*fi;
end;
s[2*k,2*k-1]:=-b2; s[2*k,2*k]:=h*b1+b2;
z[2*k]:=h*BB;
end;
procedure TForm1.FormCreate(Sender: TObject);
begin
getdir(0,str);
str:=str+'\otv\';
end;
procedure TForm1.SpeedButton1Click(Sender: TObject);
begin
if (form1.LabeledEdit1.Text='') and
(form1.LabeledEdit9.Text='') and
(form1.LabeledEdit12.Text='') then
begin
showmessage('так як ви не ввели коефіцієнти, то программа буде задіяна зі стандартним набором данних');
pi:=-1;
qi:=-2;
fi:=1;
a1:=1;
a2:=-1;
a:=0.5;
AA:=1;
b1:=1;
b2:=1;
b:=1.5;
BB:=0;
eps:=0.0001;
end
else
begin
pi:=strtofloat(form1.LabeledEdit1.Text);
qi:=strtofloat(form1.LabeledEdit2.Text);
fi:=strtofloat(form1.LabeledEdit3.Text);
a1:=strtofloat(form1.LabeledEdit4.Text);
a2:=strtofloat(form1.LabeledEdit5.Text);
a:=strtofloat(form1.LabeledEdit6.Text);
AA:=strtofloat(form1.LabeledEdit7.Text);
b1:=strtofloat(form1.LabeledEdit8.Text);
b2:=strtofloat(form1.LabeledEdit9.Text);
b:=strtofloat(form1.LabeledEdit10.Text);
BB:=strtofloat(form1.LabeledEdit11.Text);
eps:=strtofloat(form1.LabeledEdit12.Text);
end;
form2.Series1.Clear;
AssignFile(t_all,str+'otv.txt');
AssignFile(tx,str+'otv_x.txt');
AssignFile(ty,str+'otv_y.txt');
AssignFile(k_i,str+'otv_krok_vuzl.txt');
Rewrite(t_all);
m:=1;
g:=false;
While not g do
begin
h:=(b-a)/(2*m);
SetLength(y,2*m+1);
SetLength(x,2*m+1);
SetLength(d,2*m+1);
for i:=0 to 2*m do
x[i]:=a+i*h;
Setlength(c,2*m+1);
for i:=0 to 2*m do
Setlength(c[i],2*m+1);
Koef(c,m,h,x,d);
if gauss(2*m+1,c,d,y)<>true then
break;
if m<>1 then
for i:=0 to m do
if abs(memory[i]-y[2*i])/15>eps then
begin
g:=false;
break;
end
else
g:=true;
SetLength(memory,2*m+1);
memory:=Copy(y);
if g then
writeln(t_all,'Крайова задача розвязана з точністю eps =',eps:0:4);
for i:=0 to 2*m do
begin
write(t_all,y[i]:0:10);
write(t_all,' ');
writeln(t_all,x[i]:0:10);
end;
Writeln(t_all,'Кількість вузлів - ',2*m+1);
Writeln(t_all,'Крок сітки - ',h:0:10);
Writeln(t_all);
st:=m;
m:=m*2;
end;
rewrite(ty);
rewrite(tx);
rewrite(k_i);
writeln(k_i,h:0:10);
writeln(k_i,2*m+1);
form2.StringGrid1.ColCount:=2*st+2;
for i:=0 to (2*st+1) do
begin
form2.StringGrid1.Cells[i+1,0]:=inttostr(i+1);
form2.StringGrid1.Cells[i+1,1]:=floattostr(x[i]);
form2.StringGrid1.Cells[i+1,2]:=floattostr(y[i]);
writeln(ty,y[i]:0:10);
writeln(tx,x[i]:0:10);
end;
for i:=0 to (2*st) do
form2.Series1.AddXY(x[i],y[i]);
form2.Label1.Caption:='Крок сітки - '+floattostr(h);
form2.Label2.Caption:='Кількість вузлів - '+floattostr(2*st+1);
CloseFile(t_all);
CloseFile(tx);
CloseFile(ty);
CloseFile(k_i);
form2.Show;
end;
end.
Результати записуємо у файл.
Графік отриманий програмою:
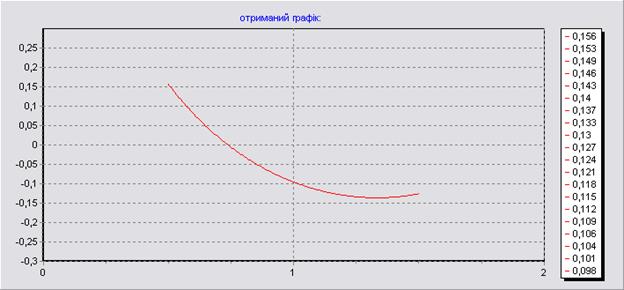
Розв’язання з використанням методу прогонки:
unit Unit1;
interface
uses
Windows, Messages, SysUtils, Variants, Classes, Graphics, Controls, Forms,
Dialogs, ExtCtrls, StdCtrls, Buttons;
type
TForm1 = class(TForm)
Panel1: TPanel;
Label1: TLabel;
Image1: TImage;
Image2: TImage;
Label2: TLabel;
LabeledEdit1: TLabeledEdit;
LabeledEdit2: TLabeledEdit;
LabeledEdit3: TLabeledEdit;
LabeledEdit4: TLabeledEdit;
LabeledEdit5: TLabeledEdit;
LabeledEdit6: TLabeledEdit;
LabeledEdit7: TLabeledEdit;
LabeledEdit8: TLabeledEdit;
LabeledEdit9: TLabeledEdit;
LabeledEdit10: TLabeledEdit;
LabeledEdit11: TLabeledEdit;
Label3: TLabel;
Label4: TLabel;
SpeedButton1: TSpeedButton;
LabeledEdit12: TLabeledEdit;
Label5: TLabel;
Image3: TImage;
procedure FormCreate(Sender: TObject);
procedure SpeedButton1Click(Sender: TObject);
private
{ Private declarations }
public
{ Public declarations }
end;
var
Form1: TForm1;
type Dynmas=array of array of real;
dynvec=array of real;
var a,b,pi,qi,fi,a1,a2,b1,b2,AA,BB:real;
eps,h:real;
c:dynmas;
st,m,i:integer;
w_,v_,x,d,y,memory:dynvec;
t_all,tx,ty,k_i:textfile;
g:boolean;
time1,time2,vremja:longint;
str:string;
implementation
uses Unit2;
{$R *.dfm}
Function Timer:longint;
const c60:longint=60;
var h,m,s,s100:word;
begin
decodetime(now,h,m,s,s100);
timer:=((h*c60+m)*c60+s)*100+s100;
end;
function progonka(n:Integer; a:dynmas; b:dynVec; var x:dynVec):boolean;
Var i,j,k,l:Integer;
q,m,t:real;
ls:integer;
Begin
{прямой ход}
w_[0]:=(-a[0,1]/a[0,0]);
v_[0]:=(d[0]/a[0,0]);
for i:=1 to n-1 do
begin
w_[i]:=-(a[i,i+1]/(a[i,i-1]*w_[i-1]+a[i,i]));
v_[i]:=(d[i]-a[i,i-1]*v_[i-1])/(a[i,i-1]*w_[i-1]+a[i,i]);
end;
{w_[n]:= ;
v_[n]:= ;}
for i:=0 to n-1 do
begin
x[i]:=v_[i]+w_[i]*x[i+1];
end;
x[n-1]:=v_[n-1];
{обратный ход}
x[n-1]:=v_[n-1];
for i:=n-1 downto 0 do
begin
x[i]:=w_[i]*x[i+1]+v_[i];
end;
{for k:=0 to n-2 do
begin
l:=-1;
m:=0;
for i:=k to n-1 do
if Abs(a[i, k])>m then
begin
m:=Abs(a[i, k]);
l:=i;
end;
if l=-1 then
begin
progonka:=false;
Exit;
end;
if l<>k then
begin
For j:=0 to n-1 do
begin
t:=a[k,j];
a[k,j]:=a[l,j];
a[l,j]:=t;
end;
t:=b[k];
b[k]:=b[l];
b[l]:=t;
end;
for i:=k+1 to n-1 do
begin
q:=a[i,k]/a[k,k];
for j:=0 to n-1 do
If j=k then
a[i,j]:= 0
else
a[i,j]:= a[i,j]-q*a[k,j];
b[i]:=b[i]-q*b[k];
end;
end;
if a[n-1,n-1]<>0 then
x[n-1]:=b[n-1]/a[n-1,n-1]
else
begin
progonka:=false;
Exit;
end;
for i:=n-2 downto 0 do
begin
t:=0;
for j:=1 to n-i do
t:=t+a[i,i+j]*x[i+j];
x[i]:=(1/a[i,i])*(b[i]-t);
end;}
progonka := true;
end;
procedure Koef(var s:dynmas; k:integer; h:real; v:dynvec; var z:dynvec);
var i:integer;
begin
s[0,0]:=h*a1-a2; s[0,1]:=a2;
z[0]:=h*AA;
for i:=0 to 2*(k-1) do
begin
s[i+1,i]:=1-(h*pi*ln(v[i]))/2;
s[i+1,i+1]:=h*h*qi-2;
s[i+1,i+2]:=1+(h*pi*ln(v[i]))/2;
z[i+1]:=h*h*fi;
end;
s[2*k,2*k-1]:=-b2; s[2*k,2*k]:=h*b1+b2;
z[2*k]:=h*BB;
end;
procedure TForm1.FormCreate(Sender: TObject);
begin
getdir(0,str);
str:=str+'\otv\';
vremja:=0;
end;
procedure TForm1.SpeedButton1Click(Sender: TObject);
begin
if (form1.LabeledEdit1.Text='') and
(form1.LabeledEdit9.Text='') and
(form1.LabeledEdit12.Text='') then
begin
showmessage('так як ви не ввели коефіцієнти, то программа буде задіяна зі стандартним набором данних');
pi:=-1;
qi:=-2;
fi:=1;
a1:=1;
a2:=-1;
a:=0.5;
AA:=1;
b1:=1;
b2:=1;
b:=1.5;
BB:=0;
eps:=0.0001;
end
else
begin
pi:=strtofloat(form1.LabeledEdit1.Text);
qi:=strtofloat(form1.LabeledEdit2.Text);
fi:=strtofloat(form1.LabeledEdit3.Text);
a1:=strtofloat(form1.LabeledEdit4.Text);
a2:=strtofloat(form1.LabeledEdit5.Text);
a:=strtofloat(form1.LabeledEdit6.Text);
AA:=strtofloat(form1.LabeledEdit7.Text);
b1:=strtofloat(form1.LabeledEdit8.Text);
b2:=strtofloat(form1.LabeledEdit9.Text);
b:=strtofloat(form1.LabeledEdit10.Text);
BB:=strtofloat(form1.LabeledEdit11.Text);
eps:=strtofloat(form1.LabeledEdit12.Text);
end;
time2:=timer;
form2.Series1.Clear;
AssignFile(t_all,str+'otv.txt');
AssignFile(tx,str+'otv_x.txt');
AssignFile(ty,str+'otv_y.txt');
AssignFile(k_i,str+'otv_krok_vuzl.txt');
Rewrite(t_all);
m:=1;
g:=false;
While not g do
begin
h:=(b-a)/(2*m);
SetLength(y,2*m+1);
SetLength(x,2*m+1);
SetLength(d,2*m+1);
SetLength(w_,2*m+1);
SetLength(v_,2*m+1);
for i:=0 to 2*m do
x[i]:=a+i*h;
Setlength(c,2*m+1);
for i:=0 to 2*m do
Setlength(c[i],2*m+1);
Koef(c,m,h,x,d);
if progonka(2*m+1,c,d,y)<>true then
break;
if m<>1 then
for i:=0 to m do
if abs(memory[i]-y[2*i])/15>eps then
begin
g:=false;
break;
end
else
g:=true;
SetLength(memory,2*m+1);
memory:=Copy(y);
if g then
writeln(t_all,'Крайова задача розвязана з точністю eps =',eps:0:4);
for i:=0 to 2*m do
begin
write(t_all,y[i]:0:10);
write(t_all,' ');
writeln(t_all,x[i]:0:10);
end;
Writeln(t_all,'Кількість вузлів - ',2*m+1);
Writeln(t_all,'Крок сітки - ',h:0:10);
Writeln(t_all);
st:=m;
m:=m*2;
end;
rewrite(ty);
rewrite(tx);
rewrite(k_i);
writeln(k_i,h:0:10);
writeln(k_i,2*m+1);
form2.StringGrid1.ColCount:=2*st+2;
for i:=0 to (2*st+1) do
begin
form2.StringGrid1.Cells[i+1,0]:=inttostr(i+1);
form2.StringGrid1.Cells[i+1,1]:=floattostr(x[i]);
form2.StringGrid1.Cells[i+1,2]:=floattostr(y[i]);
writeln(ty,y[i]:0:10);
writeln(tx,x[i]:0:10);
end;
for i:=0 to (2*st) do
form2.Series1.AddXY(x[i],y[i]);
form2.Label1.Caption:='Крок сітки - '+floattostr(h);
form2.Label2.Caption:='Кількість вузлів - '+floattostr(2*st+1);
time1:=timer;
vremja:=abs(time2-time1);
form2.Label3.Caption:='час роботи: '+floattostr(vremja*0.01)+' секунд(и)';
writeln(k_i,vremja*0.01:0:5);
CloseFile(t_all);
CloseFile(tx);
CloseFile(ty);
CloseFile(k_i);
form2.Show;
end;
end
Результати записуємо у файл.
Графік отриманий програмою:
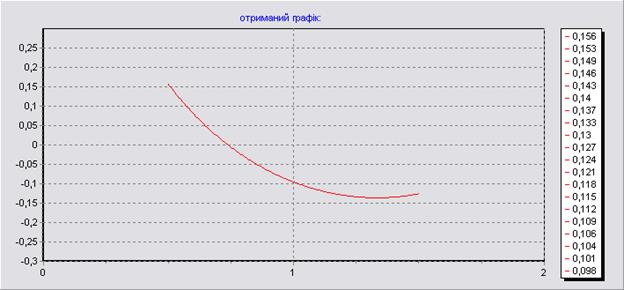
Якщо проаналізувати ці два приклади програми:
1)з використанням методу Гауса для розв’язання тридіагональної матриці;
2)з використанням методу прогонки для розв’язання тридіагональної матриці.
Ми можемо сказати, що для однієї і тієї ж задачі час розв’язання з використанням 1ого методу складає 2,99 сек., а для 2ого 0.1 сек. Така розбіжність у часі випливає з того, що метод прогону є модифікацією методу Гауса і призначений спеціально для розв’язку матриць з 3и і 5и діагональними структурами.
Розв’язуємо задачу за допомогою пакету Mathematica:

100
0.01
-0.123705
![]()
MultipleListPlot[{{0.5,0.154796},{0.51,0.146438},{0.52,0.138265},{0.53,0.130272},{0.54,0.122456},{0.55,0.114812},{0.56,0.107336},{0.57,0.100024},{0.58,0.0928731},{0.59,0.0858792},{0.6,0.079039},{0.61,0.0723491},{0.62,0.0658064},{0.63,0.0594079},{0.64,0.0531504},{0.65,0.0470312},{0.66,0.0410475},{0.67,0.0351966},{0.68,0.0294758},{0.69,0.0238829},{0.7,0.0184152},{0.71,0.0130705},{0.72,0.00784647},{0.73,0.00274101},{0.74,-0.002248},{0.75,-0.00712262},{0.76,-0.0118848},{0.77,-0.0165364},{0.78,-0.0210793},{0.79,-0.0255153},{0.8,-0.029846},{0.81,-0.0340732},{0.82,-0.0381983},{0.83,-0.0422231},{0.84,-0.0461488},{0.85,-0.049977},{0.86,-0.0537091},{0.87,-0.0573463},{0.88,-0.06089},{0.89,-0.0643414},{0.9,-0.0677017},{0.91,-0.0709721},{0.92,-0.0741536},{0.93,-0.0772473},{0.94,-0.0802542},{0.95,-0.0831754},{0.96,-0.0860117},{0.97,-0.0887641},{0.98,-0.0914334},{0.99,-0.0940204},{1.,-0.096526},{1.01,-0.0989509},{1.02,-0.101296},{1.03,-0.103561},{1.04,-0.105748},{1.05,-0.107857},{1.06,-0.109889},{1.07,-0.111844},{1.08,-0.113722},{1.09,-0.115525},{1.1,-0.117252},{1.11,-0.118904},{1.12,-0.120482},{1.13,-0.121985},{1.14,-0.123415},{1.15,-0.124771},{1.16,-0.126054},{1.17,-0.127264},{1.18,-0.128401},{1.19,-0.129466},{1.2,-0.130459},{1.21,-0.131379},{1.22,-0.132228},{1.23,-0.133004},{1.24,-0.133708},{1.25,-0.134341},{1.26,-0.134902},{1.27,-0.135391},{1.28,-0.135808},{1.29,-0.136154},{1.3,-0.136427},{1.31,-0.136628},{1.32,-0.136757},{1.33,-0.136814},{1.34,-0.136798},{1.35,-0.136709},{1.36,-0.136547},{1.37,-0.136312},{1.38,-0.136004},{1.39,-0.135621},{1.4,-0.135164},{1.41,-0.134633},{1.42,-0.134026},{1.43,-0.133344},{1.44,-0.132586},{1.45,-0.131752},{1.46,-0.130841},{1.47,-0.129852},{1.48,-0.128786},{1.49,-0.127641},{1.5,-0.126416}},{{0.5,0.159038},{0.51,0.150628},{0.52,0.142405},{0.53,0.134363},{0.54,0.126498},{0.55,0.118807},{0.56,0.111285},{0.57,0.103929},{0.58,0.0967336},{0.59,0.0896968},{0.6,0.0828146},{0.61,0.0760838},{0.62,0.0695011},{0.63,0.0630634},{0.64,0.0567678},{0.65,0.0506112},{0.66,0.0445911},{0.67,0.0387046},{0.68,0.0329491},{0.69,0.0273222},{0.7,0.0218214},{0.71,0.0164443},{0.72,0.0111888},{0.73,0.00605251},{0.74,0.00103346},{0.75,-0.00387045},{0.76,-0.00866119},{0.77,-0.0133407},{0.78,-0.0179107},{0.79,-0.0223731},{0.8,-0.0267296},{0.81,-0.0309819},{0.82,-0.0351315},{0.83,-0.0391799},{0.84,-0.0431288},{0.85,-0.0469795},{0.86,-0.0507334},{0.87,-0.0543918},{0.88,-0.0579562},{0.89,-0.0614276},{0.9,-0.0648073},{0.91,-0.0680964},{0.92,-0.0712961},{0.93,-0.0744074},{0.94,-0.0774314},{0.95,-0.0803691},{0.96,-0.0832213},{0.97,-0.085989},{0.98,-0.0886731},{0.99,-0.0912744},{1.,-0.0937936},{1.01,-0.0962317},{1.02,-0.0985892},{1.03,-0.100867},{1.04,-0.103065},{1.05,-0.105185},{1.06,-0.107227},{1.07,-0.109192},{1.08,-0.11108},{1.09,-0.112891},{1.1,-0.114627},{1.11,-0.116287},{1.12,-0.117872},{1.13,-0.119382},{1.14,-0.120819},{1.15,-0.122181},{1.16,-0.123469},{1.17,-0.124684},{1.18,-0.125825},{1.19,-0.126894},{1.2,-0.12789},{1.21,-0.128813},{1.22,-0.129664},{1.23,-0.130442},{1.24,-0.131148},{1.25,-0.131781},{1.26,-0.132342},{1.27,-0.132831},{1.28,-0.133248},{1.29,-0.133592},{1.3,-0.133863},{1.31,-0.134062},{1.32,-0.134189},{1.33,-0.134242},{1.34,-0.134222},{1.35,-0.134129},{1.36,-0.133962},{1.37,-0.133722},{1.38,-0.133407},{1.39,-0.133018},{1.4,-0.132554},{1.41,-0.132015},{1.42,-0.1314},{1.43,-0.13071},{1.44,-0.129943},{1.45,-0.129098},{1.46,-0.128177},{1.47,-0.127177},{1.48,-0.126099},{1.49,-0.124942},{1.5,-0.123705}},PlotLegend{Mathematica,Rizn method},PlotJoined{False,True},PlotPosition{0.3,-0.5}]
Отримуємо графіки:
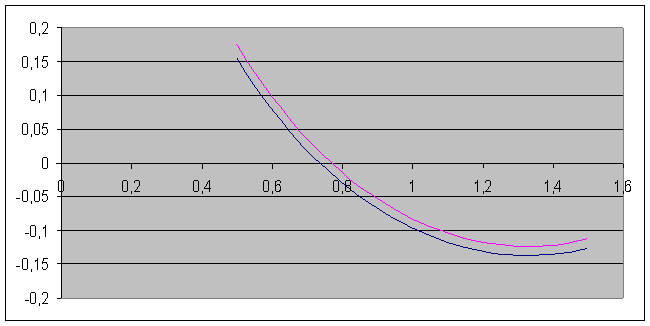
де червона – метод скінченних різниць.
синя – стандартний метод пакету Mathematica
Висновки
Крайова задача для звичайних диференціальних рівнянь є набагато складнішою, ніж задача Коші. Одним із підходів до розв'язання цієї задачі є зведення її до задачі Коші зі змінними початковими умовами. Розв'язок задачі отримують багаторазовим розв'язанням задачі Коші.
У загальному випадку для розв'язання двоточкової крайової задачі (одно- чи багатовимірної, лінійної чи нелінійної) доцільно застосовувати метод прицілювання, а для розв'язання окремих лінійних одновимірних задач — метод композиції двох розв'язків задачі Коші з різними початковими умовами.
Ефективним методом розв'язання лінійної крайової задачі для диференціального рівняння другого порядку є метод скінченних різниць, у якому використовуються різницеві схеми апроксимації для похідних першого і другого порядків. У результаті крайова задача перетворюється на задачу розв'язання системи лінійних рівнянь із тридіагональною матрицею. Цю систему можна розв'язати методом прогону.
Метод скінченних різниць дозволяє також обчислювати власні значення і власні функції крайової задачі, які визначають нетривіальні розв'язки однорідної крайової задачі.
Метод скінченних різниць можна застосовувати і для розв'язання нелінійних крайових задач, але в цьому випадку необхідно лінеаризовувати нелінійні функції, що входять в умову задачі.
Розв'язок крайової задачі у вигляді апроксимуючого аналітичного виразу отримують методами колокацій, Гальоркіна і найменших квадратів введенням базисних функцій, які враховують граничні умови.
Коефіцієнти для базисних функцій та їх композиції, які апроксимують розв'язок крайової задачі, у методі колокацій вибирають з умови нульової нев'язки в обраних вузлах інтервалу розв'язку, у методі найменших квадратів — з умови мінімуму квадрату нев'язки, а в методі Гальоркіна — з умови ортогональності нев'язки до обраних базисних функцій.
У сучасних математичних пакетах розв'язання крайових задач для рівнянь з частинними похідними конкуренцію розглянутим методам складає метод скінчених елементів, що базується на концепціях метода Гальоркіна за умови спеціального вибору базисних функцій.
Література
1.Н.С.Бахвалов, Н.П.Жидков, Г.М.Кобельков «Численные методы»
2.В.А.Буслов, С.Л.Яковлев «Численные методы ІІ.Решение уравнений».-Курс лекций,- СПб, 2001.
3.Н.Н.Калиткин «Численные методы»
4.А.А.Самарский, А.В.Гулин «Численные методы»,- Москва,- «Наука»,-1989г.
5.Б.П.Демидович, И.А.Марон, Э.Э.Шувалов «Численные методы анализа»,-ред. Б.П.Демидовича,- Москва,- «Наука»,- 1967г.