
Рефераты по авиации и космонавтике
Рефераты по административному праву
Рефераты по безопасности жизнедеятельности
Рефераты по арбитражному процессу
Рефераты по архитектуре
Рефераты по астрономии
Рефераты по банковскому делу
Рефераты по сексологии
Рефераты по информатике программированию
Рефераты по биологии
Рефераты по экономике
Рефераты по москвоведению
Рефераты по экологии
Краткое содержание произведений
Рефераты по физкультуре и спорту
Топики по английскому языку
Рефераты по математике
Рефераты по музыке
Остальные рефераты
Рефераты по биржевому делу
Рефераты по ботанике и сельскому хозяйству
Рефераты по бухгалтерскому учету и аудиту
Рефераты по валютным отношениям
Рефераты по ветеринарии
Рефераты для военной кафедры
Рефераты по географии
Рефераты по геодезии
Рефераты по геологии
Рефераты по геополитике
Рефераты по государству и праву
Рефераты по гражданскому праву и процессу
Рефераты по кредитованию
Рефераты по естествознанию
Рефераты по истории техники
Рефераты по журналистике
Рефераты по зоологии
Рефераты по инвестициям
Рефераты по информатике
Исторические личности
Рефераты по кибернетике
Рефераты по коммуникации и связи
Рефераты по косметологии
Рефераты по криминалистике
Рефераты по криминологии
Рефераты по науке и технике
Рефераты по кулинарии
Рефераты по культурологии
Курсовая работа: Двумерная кластеризая по предельному расстоянию. Дискретная математика
Курсовая работа: Двумерная кластеризая по предельному расстоянию. Дискретная математика
Федеральное агентство по образованию
ГОУ ВПО "ОМСКИЙ ГОСУДАРСТВЕННЫЙ ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ"
Кафедра «Автоматизированные системы обработки информации и управления»
ПОЯСНИТЕЛЬНАЯ ЗАПИСКА
К КУРСОВОМУ ПРОЕКТУ
по дисциплине «Дискретная математика»
ДВУМЕРНАЯ КЛАСТЕРИЗАЦИЯ ПО ПРЕДЕЛЬНОМУ РАССТОЯНИЮ
Омск – XXX
Реферат
Отчёт 14с., 1ч., 12рис., 0табл., 3источника, 0прил.
ГРАФ, КЛАСТЕР, МИНИМАЛЬНОЕ ОСТОВНОЕ ДЕРЕВО.
Предметом курсового проекта является кластеризация.
Цель работы – разработка алгоритма кластеризации по предельному расстоянию и построение минимального остовного дерева каждого кластера.
В ходе работы был разработан алгоритм кластеризации.
В результате работы было написан алгоритм, решающий данные задачи.
Введение
Часто бывает полезно и наглядно изображать некоторую ситуацию в виде рисунка, состоящего из точек (вершин) и линий (рёбер), соединяющих некоторые вершины. Такие изображения получили названия графа.
Теория графов получила широкое применение на практике. Она применяется в гражданском строительстве, электротехнике, социологии и экономике и в других областях.
Одной из задач теории графов является кластеризация и построение минимального остовного дерева. Эти задачи часто возникают на практике: при группировке результатов поиска, проектировании компьютерных систем, соединении городов, составлении электрических цепей.
Целью данной работы является разработка алгоритма, выполняющего данные задачи.
Отчет содержит четыре раздела:
- постановка задачи курсового проектирования – это раздел, в котором описывается задача курсового проекта;
- схемы алгоритмов – это раздел, в котором описывается алгоритм и его схема;
- теоретический анализ – теория, необходимая для выполнения поставленной задачи;
- результаты тестирования – это раздел, в котором описываются результаты тестирований на правильность работы разработанного алгоритма.
1 Постановка задачи курсового проектирования
Реализовать алгоритм кластеризации заданного набора точек по предельному расстоянию d. После кластеризации граф каждого кластера редуцировать до минимального остовного дерева.
2 Теоретический анализ
Граф G - это математический объект, состоящий из множества вершин X = {x1, x2,..., xn} и множества ребер A = {a1, a2,..., ak}.
Связный граф — такой граф, в котором между любой парой вершин существует по крайней мере один путь.
Взвешенный граф — граф, каждому ребру которого поставлено в соответствие некоторое значение (вес ребра).
Вес ребра — значение, поставленное в соответствие данному ребру взвешенного графа. Обычно вес — вещественное число и его можно интерпретировать как «длину» ребра.
Если ребрам графа приданы направления от одной вершины к другой, то такой граф называется ориентированным. Ребра ориентированного графа называются дугами. Если направления ребер не указываются, то граф называется неориентированным (или просто графом).
Подграф исходного графа — граф, содержащий некое подмножество вершин данного графа и некое подмножество инцидентных им рёбер.
Матрица смежности графа G с конечным числом вершин n (пронумерованных числами от 1 до n) — это квадратная матрица A размера n, в которой значение элемента ai j равно числу ребёр из i-й вершины графа в j-ю вершину.
Матрица смежности простого графа является бинарной матрицей и содержит нули на главной диагонали.
Кластерный анализ — задача разбиения заданной выборки объектов (ситуаций) на подмножества, так, чтобы каждый кластер состоял из схожих объектов, а объекты разных кластеров существенно отличались.
Кластер — группа элементов, характеризуемых общим свойством.
В данном случае в кластеры объединяются точки, находящиеся на расстоянии меньше предельного d.
Лес — неориентированный граф без циклов. Компонентами связности леса являются деревья.
Дерево — это связный граф, не содержащий циклов.
Минимальное остовное дерево (или минимальное покрывающее дерево) в связанном, взвешенном, неориентированном графе — это остовное дерево, имеющее минимальный возможный вес. Вес дерева — сумма весов входящих в него рёбер.
В данном курсовом проекте для построения минимального остовного дерева используется алгоритм Краскала. Рёбра графа упорядочиваются в порядке не убывания их весов и последовательно добавляются к графу. Если добавление нового ребра приведёт к образованию цикла, то это ребро пропускается. Подграф данного графа, содержащий все его вершины и найденное множество рёбер, является его остовным лесом минимального веса.
3 Схемы основных алгоритмов
3.1 Пошаговый алгоритм
Шаг 1. Заполнение матрицы весов T.
Шаг 2. Создание матрицы смежности С.
Шаг 2а. Если расстояние между двумя точками s > d, то в матрицу заносится 0, иначе 1.
Шаг 2б. Повторение шага 2 N раз;
Шаг 3. Создание матрицы минимального остовного дерева ТТ;
Шаг 3а. Если ttii = 0, ttjj = 0, то ttij = tij, ttii = k, ttjj = k, k = k +1, где tij – минимальный положительный элемент матрицы T;
Шаг 3б. Если ttii = 0, ttjj ≠ 0, то ttij = tij, ttii = ttjj;
Шаг 3д. Если ttii ≠ 0, ttjj = 0,то ttij = tij, ttjj = ttii;
Шаг 3е. Если ttii ≠ 0, ttjj ≠ 0, ttii ≠ ttjj ,то ttij = tij, ttii = l, ttjj = l, где l – наименьшее из ttii и ttjj;
Шаг 3ж. Если ttii ≠ 0, ttjj ≠ 0, ttii = ttjj, то tij = -1;
Шаг 4. Проверка диагональных элементов матрицы ТT;
Шаг 4б. Если ttzz = 1, то повторить шаг 4. Иначе m = 0;
Шаг 5. Повторять алгоритм с шага 3 до тех пор, пока m ≠ 1;
3.2 Схема алгоритма.
Решение данной задачи состоит из нескольких этапов: кластеризации и построения минимального остовного дерева. Схемы этих алгоритмов, изображены на рисунках 2 – 4. Общая схема алгоритма изображена на рисунке 1.
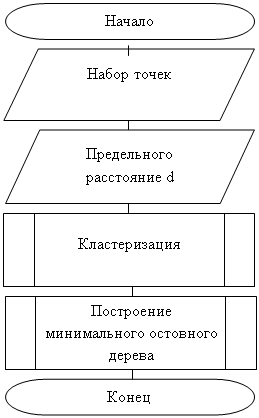
Рисунок 1 – Схема основного алгоритма

Рисунок 2 – Алгоритм кластеризации
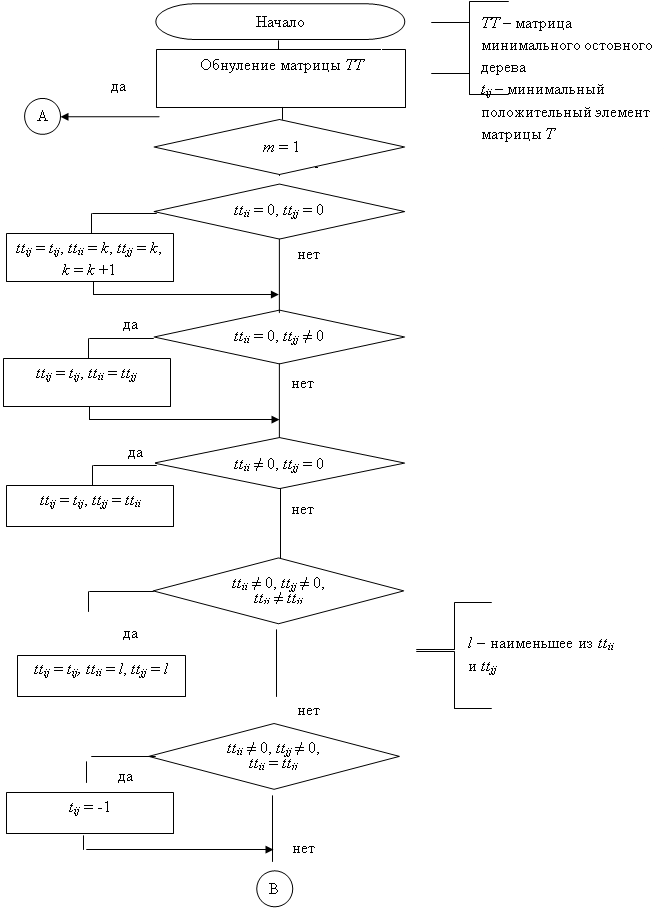
Рисунок 3 – Алгоритм построения минимального остовного дерева
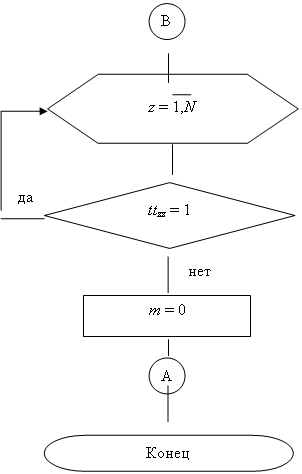
Рисунок 4 – Алгоритм построения минимального остовного дерева (продолжение)
4 Результаты тестирования
Было проведено 3 различных эксперимента.
4.1 Тест первый.
Пусть граф содержит 8 вершин, координаты которых заданы случайным образом, а взвешенная матрица Т представлена на рисунке 5. Предельное расстояние d = 5;
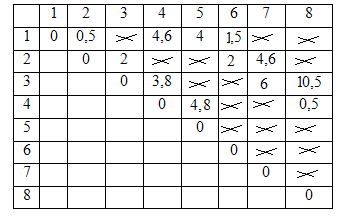
Рисунок 5 – Тест первый (часть 1)
Шаг 1. Обнуление матрицы дерева ТТ.
Шаг 2. Составляем матрицу смежности С.
Шаг 2а. Если расстояние между двумя точками s > d, то в матрицу заносится 0, иначе 1.
Шаг 2б. Повторение шага 2 8 раз. Полученная в результате матрица смежности представлена на рисунке 6.
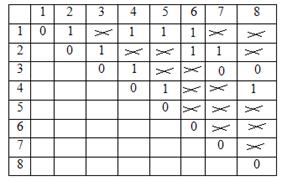
Рисунок 6 – Тест первый (часть 2)
Шаг 3. Составляем матрицу дерева ТТ.
Шаг 3а. Первоначально в матрице на главной диагонали все нули, значит
tt11 = tt22 = ... = tt88 = 0, k = 1;
Шаг 3б. Находим минимальный элемент матрицы Т - t12 = 0,5. Включаем данное ребро в матрицу ТТ и увеличиваем значение счётчика k = k + 1 = 2;
Шаг 3г. Находим следующий минимальный элемент и повторяем все действия из шага 3б. Таким образом перебираем всю матрицу.
Шаг 4. На главной диагонали матрицы ТТ находятся все 1. Полученная матрица представлена на рисунке 7.

Рисунок 7 – Тест первый (часть 3)
4.1 Тест второй.
Результат выполнения алгоритма с 20-ю вершинами, заданными случайными координатами и предельным расстоянием равным 2,5 представлен на рисунке 8.
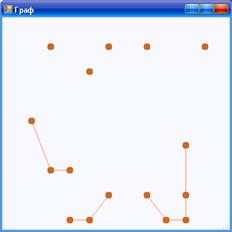
Рисунок 8 – Тест второй (часть 1)
На данном рисунке видно, что граф был разбит на 8 кластеров. Увеличим предельное расстояние до 3. Из рисунка 9 видно, что количество кластеров сократилось до 4.
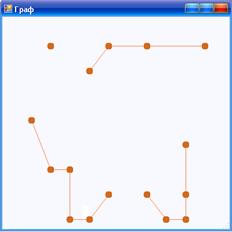
Рисунок 9 – Тест первый (часть 2)
Продолжая постепенно увеличивать предельное расстояние, увидим, что в итоге граф будет представлять собой один кластер. Минимальное остовное дерево этого кластера представлено на рисунке 10.
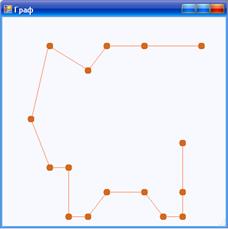
Рисунок 10 – Тест первый (часть 3)
Из этого теста видно, что с увеличением предельного расстояния количество кластеров уменьшается. Минимальное остовное дерево строится верно. Значит, в данном тесте программа работает верно.
4.3 Тест третий
Составим граф из 7 вершин, координаты которых и предельное расстояние представлены на рисунке 11.

Рисунок 11 – Тест второй (часть 1)
Построим данный граф. Остовное дерево данного графа, а так же матрицы смежности, расстояний и остовного дерева представлены на рисунке 12.
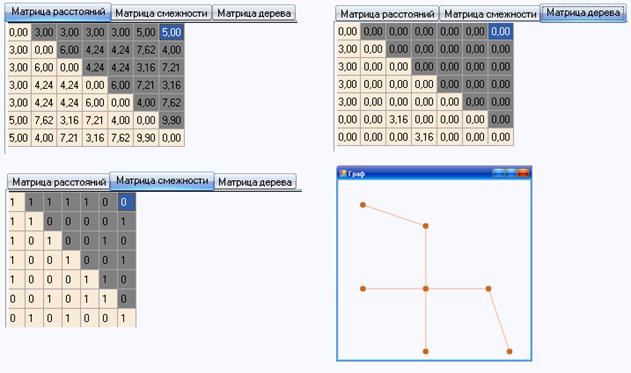
Рисунок 12 – Тест второй (часть 2)
Заключение
При рассмотрении данной задачи был изучен один из разделов теории графов кластеризация и построение минимального остовного дерева по алгоритму Краскала.
Результатом курсового проекта является алгоритм, выполняющий необходимые задачи.
Список использованных источников
1 Канева О.Н. Дискретная математика. – Омск: ОмГТУ, 2009. -87с.
2 Кристофидес Н. Теория графов. Алгоритмический подход.- М.: Мир, 1978.-433с.
3 Новиков Ф.А. Дискретная математика для программистов. – СПб: Питер, 2000. -304с.