Курсовая работа: Рівномірне наближення функцій ермітовими сплайнами

Курсовая работа: Рівномірне наближення функцій ермітовими сплайнами

Міністерство освіти і науки України

Національний університет "Львівська політехніка"

Курсова робота

на тему:

"Рівномірне наближення функцій ермітовими сплайнами"

Львів 2009р

Зміст

Вступ

1. Означення ермітових сплайнів з експоненціальними ланками

2. Знаходження аналітичних виразів для параметрів сплайна з експоненціальною ланкою

3. Многочленні ермітові сплайни

4. Похибки наближення ермітовими сплайнами

5. Рівномірне наближення ермітовими сплайнами

Висновок

Список використаної літератури

Додаток

Вступ

Наближення функцій необхідне для практичних розрахунків під час проведення наукових досліджень і в багатьох областях техніки. Аналітично задані функції, які представлені складним виразом, часто необхідно замінити простішим виразом, так, щоб зберігались їх властивості. Це потрібно для обчислення функцій на ЕОМ.

Методи інтерполювання многочленом Лагранжа або Ньютона на відрізку  при використанні великої кількості вузлів інтерполяції часто призводять до поганого наближення, що пояснюється значним накопиченням похибки під час обчислень. Крім того, через розбіжність процесу інтерполяції збільшення кількості вузлів не обов’язково приводить до підвищення точності.

Ще одним із способів інтерполювання на відрізку є інтерполювання з використанням сплайн функцій. Сплайн функцією або сплайном називають кусково-поліноміальну функцію, що визначена на відрізку  разом з певним числом неперервних похідних.

Перевага сплайнів над звичайною інтерполяцію є, по-перше, їх збіжність і, по-друге, стійкість процесу обчислення.

Ряд задач вимагає наближення не тільки самої функції, а й її похідних. Для цього використовують ермітові сплайни. З метою покращення точності наближення функцій сплайнами як ланки можна використовувати не тільки многочлени, а й нелінійні за параметрами вирази.

1. Означення ермітових сплайнів з нелінійним за параметрами виразами в ланках

Наведемо означення ермітових сплайнів з нелінійними за параметрами виразами в ланках (далі нелінійні ермітові сплайни) з парною і непарною кількістю параметрів.

На множині  задані значення функції  та її похідних до - го порядку включно. Потрібно побудувати ермітовий сплайн (тобто вирази для параметрів ланки) з експоненціальною ланкою:

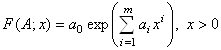 (1)

де  - параметри ланки сплайна;  - кількість параметрів .

Означення 1. Нехай . На множині  задані значення функції  та її похідних до - го порядку включно. Нелінійним ермітовим сплайном з парною кількістю параметрів  називатимемо функцію

 , (2)

яка задовольняє систему рівнянь

 , (3)

де - параметри сплайна на -й ланці; - функція Хевісайда:

Із системи (3) випливає, що . Вираз  називається ланкою ермітового сплайна. Похибка наближення функції  за допомогою ермітового сплайна  характеризується зваженою віддаллю (функцією похибки)

. (4)

Означення 2. Нехай . На множині  задані значення функції  та її похідних до - го порядку включно, а на множині  задані значення функції . Нелінійним ермітовим сплайном з непарною кількістю параметрів  називатимемо функцію виду (2), яка задовольняє систему рівнянь:

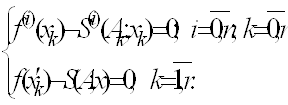 (5)

Із означень випливає, що для визначення параметрів кожної ланки конкретного нелінійного ермітового сплайна необхідно розв’язати систему рівнянь (3) або (5).

2. Вивід формул для параметрів ермітових сплайнів з експоненціальними ланками

Сімейство цих ермітових сплайнів має ланку, яку подано виразом (1). Оскільки наближаючий вираз (1) не змінює знака, то цим виразом можна наближати функції, що не змінюють знака. Припустимо для конкретності, що . Побудуємо ланки ермітового сплайна при .

При  отримаємо ермітовий сплайн з парною кількістю параметрів .

Ланка такого сплайна має вигляд

. (6)

Згідно означення 1 параметри ланки ермітового сплайна (2) з ланкою (6) задовольняють системі рівнянь (3)

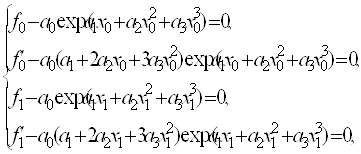 (7)

де - ліва, а - права границі ланки; ,. Розв’яжемо систему (7) щодо невідомих .

Із першого і третього рівнянь системи знаходимо вирази для параметра :

 (8)

Прирівнюємо між собою вирази для  і отримаємо вираз для :

 (9)

Підставляємо перший вираз для  і вираз для в друге рівняння системи (7) і отримаємо

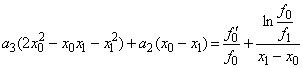 (10)

Підставляємо другий вираз для  і вираз для в четверте рівняння системи (7) і отримаємо

 (11)

Ми отримали систему двох лінійних рівнянь (10) і (11) щодо двох невідомих . Розв’язавши її, отримаємо

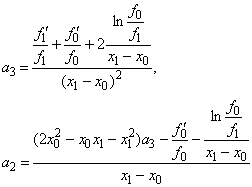 (12)

Із формул (8), (9), (10) для параметрів випливає, що необхідною умовою існування наближення ермітовим сплайном з ланкою (7) є виконання умови.

При отримаємо ермітовий сплайн з непарною кількістю параметрів . Ланка такого сплайна має вигляд

 (13)

Згідно з означенням 2 параметри ланки (13) ермітового сплайна (2) задовольняють системі рівнянь (5):

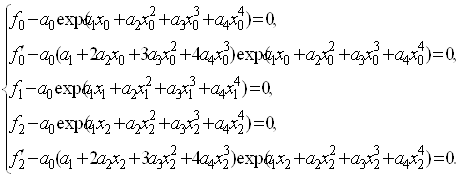 (14)

де . Розв’яжемо систему (14) щодо невідомих . Із першого, третього і четвертого рівнянь системи (14) знайдемо вирази для

. (15)

Прирівняємо вирази для (15) із першого і четвертого та першого і третього рівнянь системи (14), отримаємо два вирази для

 , (16)

 . (17)

Прирівнявши між собою вирази для  із (16) і (17), отримаємо рівняння

 (18)

Де

Підставивши перший вираз для (15) і перший вираз для (16) в друге рівняння системи (14) отримаємо рівняння

 (19)

Де

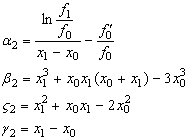
Підставивши третій вираз для (15) і перший вираз для (16) в п’яте рівняння системи (14) отримаємо рівняння

 (20)

де

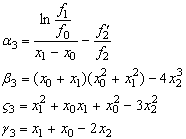
Ми отримали систему трьох лінійних рівнянь (18-20) щодо трьох невідомих . Розв’язавши її отримаємо

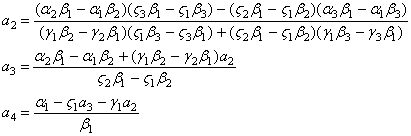 (21)

Із формул (15), (16), (17) і (21) для параметрів  випливає, що необхідною умовою існування наближення ермітовим сплайном з ланкою (13) є виконання умови .

3. Многочленні ермітові сплайни

При  отримаємо ермітовий сплайн з парною кількістю параметрів .

Ланка такого сплайна має вигляд

 . (22)

Означення 3. Нехай ,  - многочлен 3-го степеня На множині  задані значення функції  та її похідної. Кубічним ермітовим сплайном називатимемо функцію з ланкою (22)

 , (23)

яка задовольняє систему рівнянь

 (24)

де - параметри сплайна на -й ланці;

Згідно означення 3 параметри ланки ермітового сплайна (23) з ланкою (22) задовольняють системі рівнянь (24)

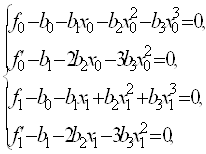 (25)

де - ліва, а - права границі ланки; ,. Розв’яжемо систему (25) щодо невідомих . Отримаємо формули для обчислень значень параметрів:

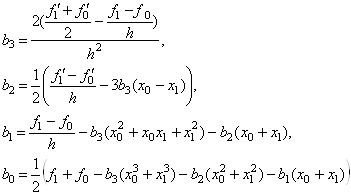 (26)

При отримаємо ермітовий сплайн з непарною кількістю параметрів . Ланка такого сплайна має вигляд

 (27)

Означення 4. Нехай ,  - многочлен 4-го степеня. На множині  задані значення функції  та її похідних до - го порядку включно, а на множині  задані значення функції . Многочленним ермітовим сплайном 4-го степеня називатимемо функцію виду (3), яка задовольняє систему рівнянь

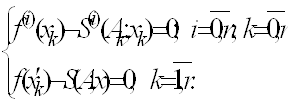 (28)

Згідно з означенням 4 параметри ланки (27) ермітового сплайна (23) задовольняють системі рівнянь (28):

 (29)

де . Розв’яжемо систему (29) щодо невідомих . Із першого, третього і четвертого рівнянь системи (29) знайдемо вирази для

. (30)

Прирівняємо вирази для (31) із першого і четвертого та першого і третього рівнянь системи (29), отримаємо два вирази для

 (31)

 (32)

Прирівнявши між собою вирази для  із (32) і (33), отримаємо рівняння

 (33)

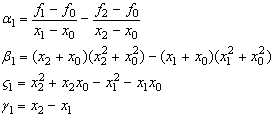
Підставивши перший вираз для (30) і перший вираз для (31) в друге рівняння системи (29) отримаємо рівняння

 (34)

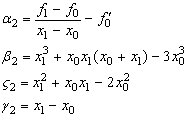
Підставивши третій вираз для (30) і перший вираз для (31) в п’яте рівняння системи (30) отримаємо рівняння

 (35)

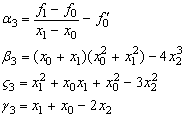
Ми отримали систему трьох лінійних рівнянь (23-35) щодо трьох невідомих . Розв’язавши її отримаємо

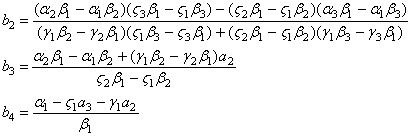 (36)

Із формул (30), (31), (32) і (36) для параметрів  випливає, що необхідною умовою існування наближення ермітовим сплайном з ланкою (27) є виконання умови .

4. Похибки наближення ермітовими сплайнами

Максимальна похибка  рівномірного наближення нелінійними ермітовими сплайнами з парною кількістю параметрів у ланці має вигляд

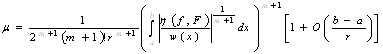, (37)

а для ермітових сплайнів з непарною кількістю параметрів

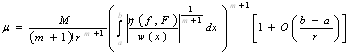 (38)

де  - кількість ланок сплайна на інтервалі , - вагова функція,  - ядро похибки наближення,  - дефект ермітового сплайна, . Для ермітового сплайна з ланкою (13) кількість параметрів , дефект сплайна за означенням , величина . Щоб скористатись формулами (37) і(38), потрібно мати вираз для ядра похибки наближення , який би не залежав від параметрів ланки сплайна . Вирази для конкретних ядер можна знайти, використовуючи властивості ядер похибок, які випливають із обмінних теорем.

Теорема 1. Нехай для функції   при  існує єдине наближення ермітовим сплайном з парною кількістю параметрів з вузлами  і ланками вигляду

 (39)

Тоді для функції  на проміжку  з тими ж вузлами існує єдине наближення ермітовим сплайном з парною кількістю параметрів і ланками вигляду

 (40)

Нехай  — найбільша відносна похибка наближення функції  на проміжку  ермітовим сплайном з ланкою (39), а  — найбільша відносна похибка наближення функції  на проміжку  ермітовим сплайном з ланкою вигляду (40). В цьому випадку між параметрами наближень мають місце співвідношення;

 (41)

. (42)

Доведення. Сплайн з ланкою вигляду (39) характеризується системою рівнянь

 (43)

а сплайн з ланкою вигляду (40) — системою рівнянь

 (44)

Надалі опускаємо індекс, який вказує на приналежність параметра до -ї ланки. Із системи (44) при  матимемо

.

Подамо  як , про логарифмуємо це рівняння і отримаємо

,

де . Тобто при  рівняння із системи (44) зведене до рівняння із системи (43).

При рівняння із системи (44) має вигляд

.

Помножимо чисельник і знаменник цього рівняння на

.

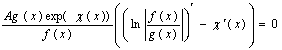Оскільки з умов теореми  не дорівнюють нулю, то рівність досягається за умови, що

,

а це і є рівняння із системи (43) при .

Використовуючи метод математичної індукції, покажемо, що рівняння із системи (44) зводиться до рівнянь із системи (43) за довільних . Нехай це доведено для . Доведемо для . Рівняння із системи (43) при :

.

Для  рівняння із системи (44) має вигляд

.

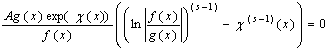Про диференціюємо це рівняння і отримаємо

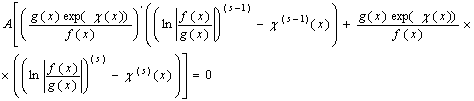
Перший доданок в квадратних дужках дорівнює нулю через рівність нулю останнього співмножника. Рівняння набере вигляду

.

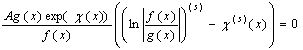Множник, який стоїть перед квадратними дужками, не дорівнює нулю з умов теореми, отже нулю дорівнює вираз у квадратних дужках. А це і є рівняння із системи (43). Отже, ми довели, що за довільних  рівняння в системах (43) і (44) еквівалентні, а , значить, і системи рівносильні. Тому  при , а .

Доведемо справедливість відношення (43) для похибок наближення. Оскільки системи (43) і (44) рівносильні, то точки, в яких досягається максимальні похибки, збігаються. Нехай точка , в якій досягається максимальна похибка наближення функції  ермітовим сплайном з ланкою (39). Тоді похибка в цій точці дорівнює

.

Із цієї рівності випливає, що

.

У правій частині маємо відносну похибку наближення функції  ермітовим сплайном з ланкою (40) на проміжку . Звідси . Теорема доведена.

За допомогою цієї теореми можна отримувати наближення ермітовим сплайном з ланкою (40) шляхом знаходження наближення ермітовим сплайном з простішою ланкою (39). Зокрема, наближення до функції  ермітовим сплайном з ланкою вигляду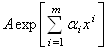 зводиться до наближення функції  ермітовим сплайном з ланкою . При цьому найбільша відносна похибка першого наближення виражається через найбільшу абсолютну похибку другого наближення.

Теорема 2. Нехай для функції    при  існує єдине наближення ермітовим сплайном з непарною кількістю параметрів з вузлами  і ланками вигляду

 (45)

Тоді для функції  на проміжку  з тими ж вузлами існує єдине наближення ермітовим сплайном з непарною кількістю параметрів і ланками вигляду

 (46)

Нехай  — найбільша відносна похибка наближення функції  на проміжку  ермітовим сплайном з ланкою (45), а  — найбільша відносна похибка наближення функції  на проміжку  ермітовим сплайном з ланкою вигляду (45). В цьому випадку між параметрами наближень мають місце співвідношення;

 (47)

.  (48)

Доведення. В теоремі 1 до системи рівнянь (42) додається рівняння

 , (49)

а до системи (43) рівняння

 (50)

Для доведення цієї теореми для ермітових сплайнів з непарною кількістю параметрів необхідно довести еквівалентність рівнянь (48) і (50). Для цього перепишемо (50) у вигляді

.

Про логарифмуємо і отримаємо

,

де із умови теореми 2 , а .Тобто рівняння (50) зведено до (49). Теорему доведено.

Властивість 1. Нехай при . Тоді

 (51)

Доведення. Із теорем 1 і 2 випливає, що наближення функції  на  ермітовим сплайном з ланкою  може бути знайдено через наближення функції  на цьому проміжку ермітовим сплайном з ланкою . При цьому із формули (42) випливає, що максимальна відносна похибка  першого наближення виражається через максимальну абсолютну похибку другого наближення

Із рівності похибок і формули (37) матимемо

.

Цей вираз справедливий для довільних  ,  і проміжків  лише в тому випадку, якщо підінтегральні вирази рівні між собою. Із їх рівності випливає вираз (51).

Тепер можна вивести аналітичний вираз для ядра похибки наближення  ермітовим сплайном з ланкою (1). Ядро похибки наближення многочленом степеня має вигляд . Застосувавши формулу (52), отримаємо

 . (52)

Для ермітового сплайна з експоненціальною ланкою (6) ядро матиме такий вигляд:

.

А для ланки (13)

5. Рівномірне наближення ермітовими сплайнами

Наближення функції ермітовим сплайном називаємо рівномірним наближенням з заданою похибкою , якщо  , де - вага наближення,.

Алгоритм рівномірного наближення ермітовими сплайнами з заданою похибкою. Алгоритм не залежить від виду сплайна.

1.  Будуємо ланку нелінійного ермітового сплайна на всьому інтервалі . Ліва границя  права

2.  Знаходимо похибку наближення .

3.  Якщо, то наближення побудоване. Кінець.

4.  Якщо , то зсуваємо праву границю інтервалу вліво, поки похибка на даному інтервалі не стане меншою від заданої похибки . Допустимо, що при -му зсуві границі вліво (т. )похибка рівна , а на попередньому кроці ( права границя ). Тоді можна знайти таку праву границю , при якій похибка  буде як завгодно мало відрізнятися від заданої . Точку  можна знайти одним із відомих способів, наприклад методом ділення відрізка навпіл або методом хорд.

5.  Запам’ятовуємо границі ланки і параметри ермітового сплайна.

6.  Лівою границею наступної ланки є права границя попередньої ланки. Правою границею можна завжди вважати т. , але можна також екстраполювати точкою  де - довжина попередньої ланки.

7.  Будуємо сплайн і знаходимо похибку.

8.  Якщо , то переходимо до пункту 4.

9.  Якщо і , то  і переходимо до пункту 7. В протилежному випадку, при , запам’ятовуємо границі та параметри нелінійного ермітового сплайна. Рівномірне наближення з заданою похибкою знайдено.

Очевидно, що описаний алгоритм приводить до єдиного рішення, якщо наближувана функція  і сплайн такі що функція похибки

,

є неспадною функцією від . Для цього достатньо, щоб ядро наближення  при .

Із означення ермітового сплайна можна запропонувати інший алгоритм знаходження його параметрів. При (парна кількість параметрів) параметри визначаються із тих же рівнянь, що й у випадку фіксованих вузлів, до яких додаються рівняння для точки екстремумуі правої границі .

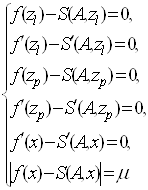 (53)

Потрібно знайти залежність  від . Для деяких вузлів ланок ермітових сплайнів, а саме ланок у вигляді многочлена, відношення многочлена до лінійної функції, добутку степеневої і експоненціальної функцій, степеневого виразу від многочлена параметри  сплайна знаходяться в аналітичному вигляді із перших чотирьох рівнянь системи (53).

Вони залежать від  і значень функції та її похідної в цих точках. Коефіцієнти можна підставити в п’яте і шосте рівняння системи. В результаті система шести рівнянь з шістьома невідомими зводиться до системи двох рівнянь з двома невідомими :

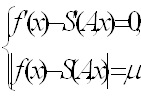 (54)

Система (54) є системою трансцендентних рівнянь. Її можна розв’язати, використовуючи відомі наближені методи знаходження коренів трансцендентних систем.

Висновки

В багатьох технічних задачах використовується кускова апроксимація однозначних функцій. Застосування у такій задачі нелінійних виразів з метою наближення викликає труднощі через відсутність ефективних алгоритмів для визначення їх параметрів. Для цієї задачі є зручними кускові наближення (сплайн-наближення). У роботі наведений приклад побудови ермітового сплайна з експоненціальною і многочленною ланками. Оскільки похибка ермітового сплайна з експоненціальною ланкою в деяких випадках є меншою, ніж у многочленного ермітового сплайна, то їх доцільно застосовувати для наближення функцій. Також побудовано алгоритми рівномірного наближення ермітовими сплайнами.

Викладацька практика

1.10.2009 – 3 пара.

Лекція з курсу "Теорія масового обслуговування".

Тема: "Потоки Пальма".

Заняття проводилось для груп СІМ51 магістри і спеціалісти.

2.10.2009 – 1 пара.

Лабораторна робота з курсу "Чисельні методи".

Тема: "Однокрокові методи чисельного розвязування задачі Коші для звичайних диференціальних рівнянь"

Заняття проводилось для групи ПМ41.

2.10.2009. – 3 пара.

Практичне заняття з курсу "Теорія масового обслуговування".

Тема: "Найпростіший потік"

Заняття проводилось для груп СІМ51 магістри і спеціалісти.

Опис програми

Програма Hermit’s spline шукає балансне наближення функцій ермітовими сплайнами. Головне вікно програми розділене на дві частини: ліву і праву. У лівій частині є три закладки: перша призначена для виводу результатів програми, друга для виводу графіків функції і сплайну; третя для виводу графіку похибки наближення. У правій частині є поля для вводу меж інтервалу і похибки. Також є перемикачі для вибору виду сплайна і функції.

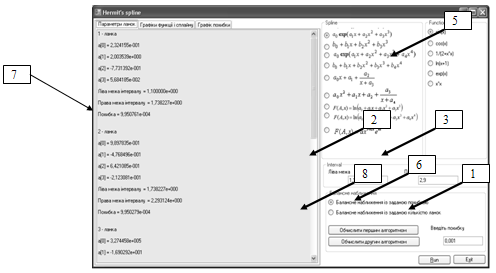
Для роботи програми треба виконати наступні дії:

·  у поля "2" "3" потрібно ввести межі інтервалу на якому функція визначена і диференційовна;

·  у поле "1" треба ввести похибку;

·  вибрати вид сплайна 4;

·  вибрати функцію 5;

·  далі натиснути кнопку "6", яка викликає функцію, що будує балансне наближення із заданою похибкою;

·  для побудови балансного наближення із заданою кількістю ланок треба натиснути кнопку "8";

·  вивід результатів буде у полі "7";

·  щоб переглянути графіки функції і сплайну потрібно натиснути на закладку 9;

·  щоб переглянути графік похибки наближення потрібно натиснути на закладку 10;

Опис основних функцій програми:

·  void ermit_1(double *a, double x0, double x1); - функція пошуку коефіцієнтів ермітового сплайна з ланками виду ;

·  void ermit_2(double *a, double x0, double x1); - функція пошуку коефіцієнтів ермітового сплайна з ланками виду ;

·  void ermit_3(double *a, double x0, double x2); - функція пошуку коефіцієнтів ермітового сплайна з ланками виду ;

·  void ermit_4(double *b, double x0, double x2); - функція пошуку коефіцієнтів ермітового сплайна з ланками виду ;

·  void ermit_5(double *a, double zl, double zp); - функція пошуку коефіцієнтів ермітового сплайна з ланками виду;

·  void ermit_rp(double *a, double a1, double b1, double nyu, int n); - рівномірне наближення ермітовими сплайнами із заданною похибкою;

·  void ermit_rl (double*a, double zl, double b1, int n, int p, int r); - рівномірне наближення ермітовими сплайнами із заданною кількістю ланок.

Література

1.  Пізюр Я.В., Попов Б.О. Рівномірне наближення ермітовими сплайнами з парною кількістю параметрів.// Контрольно-вимірювальна техніка.- 1993. – Вип. 50. – С. 8-13

2.  Пізюр Я.В. Наближення функцій ермітовими сплайнами з експоненціальними ланками// Вісник НУ "Львівська політехніка". "Фізико-математичні науки" №566, 2006, – С. 68-75.

3.  Зав’ялов Ю.С., Квасов Б.И., Мірошниченко В.Л. Методи сплайн функцій. – М.: Наука, 1980. – 352 с.

Додаток

Код програми.

private: System::Void button2_Click(System::Object^ sender, System::EventArgs^ e) {

double zl, zp, x;

zl=Double::Parse(textBox3->Text);

zp=Double::Parse(textBox4->Text);

x =(zl+zp)/2;

int p=2,n=5;

if((s1->Checked==true)||(s2->Checked==true)||(s5->Checked==true)||(s7->Checked==true)||(s9->Checked==true)){

n=4;p=1;

}

double *a = new double[n];

if (s1->Checked == true) {

ermit_1(a, zl, zp, p);

}

if (s2->Checked == true) {

ermit_2(a, zl, zp, p);

}

if (s3->Checked == true) {

ermit_3(a, zl, zp, p);

}

if (s4->Checked == true) {

ermit_4(a, zl, zp, p);

}

if (s5->Checked == true) {

ermit_5(a, zl, zp, p);

}

if (s6->Checked == true) {

ermit_6(a, zl, zp, p);

}

if (s7->Checked == true) {

ermit_8(a, zl, zp, p);

}

if (s8->Checked == true) {

ermit_9(a, zl, zp, p);

}

if (s9->Checked == true) {

ermit_7(a, zl, zp, p);

}

chart1->Series["Function"]->Points->Clear();

chart1->Series["Spline"]->Points->Clear();

chart2->Series["error"]->Points->Clear();

double t,ch1,ch2,ch3;

for(t = zl; t <= zp; t += 0.01)

{

ch1 = f(t,1);

ch2 = sp(a,t);

ch3 = epx_p(a,t,1);

chart1->Series["Function"]->Points->AddXY(t, ch1);

chart1->Series["Spline"]->Points->AddXY(t, ch2);

chart2->Series["error"]->Points->AddXY(t, ch3);

}

}

//~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~

double epx_p(double *a, double x, int p) {

return Math::Abs((f(x, p) - sp(a, x)) / w(x));

}

//~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~

public: double f(double x, int p) {

if(f1->Checked==true){

return Math::Sin(x);

}

if(f2->Checked==true){

return Math::Cos(x);

}

if(f3->Checked==true){

return 1 / (2 + x * x);

}

if(f4->Checked==true){

return Math::Log(x + 1);

}

if(f5->Checked==true){

return Math::Exp(x);

}

if(f6->Checked==true){

return x*x;

}

return -1;

}

//~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~

public: double fp(double x, int p) {

if(f1->Checked==true){

return Math::Cos(x);

}

if(f2->Checked==true){

return -Math::Sin(x);

}

if(f3->Checked==true){

return (-2* x ) / ((2 + x * x) * (2 + x * x));

}

if(f4->Checked==true){

return 1 / (x + 1);

}

if(f5->Checked==true){

return Math::Exp(x);

}

if(f6->Checked==true){

return 2*x;

}

return -1;

}

//*****************************************

public: void ermit_1(double *a, double x0, double x1, int p) {

a[3] = (fp(x1, p) / f(x1, p) + fp(x0, p) / f(x0, p) + 2 * (Math::Log(f(x0, p)

/ f(x1, p)) / (x1 - x0))) / ((x1 - x0) * (x1 - x0));

a[2] = ((2* x0 * x0 - x0 * x1 - x1 * x1) * a[3] - (fp(x0, p) / f(x0, p))

- (Math::Log(f(x0, p) / f(x1, p)) / (x1 - x0))) / (x1 - x0);

a[1] = (1 / (x1 - x0)) * (Math::Log(f(x1, p) / f(x0, p)) - a[3] * (x1 * x1 * x1

- x0 * x0 * x0) - a[2] * (x1 * x1 - x0 * x0));

a[0] = f(x0, p) * Math::Exp(-(a[1] * x0 + a[2] * x0 * x0 + a[3] * x0 * x0 * x0));

}

/////////////////////////////////////////////////////////////////////////////

void ermit_2(double *b, double x0, double x1, int p) {

double h;

h = x1 - x0;

b[3] = 2 * ((fp(x1, p) + fp(x0, p)) / 2 - (f(x1, p) - f(x0, p)) / h) / (h

* h);

b[2] = 0.5 * ((fp(x1, p) - fp(x0, p)) / h - 3* b [3] * (x0 + x1));

b[1] = fp(x1, p) - 2* b [2] * x1 - 3* b [3] * x1 * x1;

b[0] = 0.5 * (f(x1, p) + f(x0, p) - b[3] * (x0 * x0 * x0 + x1 * x1 * x1)

- b[2] * (x0 * x0 + x1 * x1) - b[1] * (x0 + x1));

}

////////////////////////////////////////////////////////////////

void ermit_3(double *a, double x0, double x2, int p) {

double a1, a2, a3, b1, b2, b3, z1, z2, z3, g1, g2, g3;

double x1;

x1 = (x0 + x2) / 2;

a1 = Math::Log(f(x1, p) / f(x0, p)) / (x1 - x0) - Math::Log(f(x2, p) / f(x0, p)) / (x2 - x0);

b1 = (x1 + x0) * (x1 * x1 + x0 * x0) - (x2 + x0) * (x2 * x2 + x0 * x0);

z1 = x1 * x1 + x1 * x0 - x2 * x2 - x2 * x0;

g1 = x1 - x2;

a2 = Math::Log(f(x1, p) / f(x0, p)) / (x1 - x0) - fp(x0, p) / f(x0, p);

b2 = x1 * x1 * x1 + x0 * x1 * (x0 + x1) - 3* x0 * x0 * x0;

z2 = x1 * x1 + x0 * x1 - 2* x0 * x0;

g2 = x1 - x0;

a3 = Math::Log(f(x1, p) / f(x0, p)) / (x1 - x0) - fp(x2, p) / f(x2, p);

b3 = (x0 + x1) * (x0 * x0 + x1 * x1) - 4* x2 * x2 * x2;

z3 = x1 * x1 + x0 * x1 + x0 * x0 - 3* x2 * x2;

g3 = x1 + x0 - 2* x2 ;

a[2] = ((a2 * b1 - a1 * b2) * (z3 * b1 - z1 * b3) - (z2 * b1 - z1 * b2)

* (a3 * b1 - a1 * b3)) / ((g1 * b2 - g2 * b1) * (z1 * b3 - z3 * b1)

+ (z2 * b1 - z1 * b2) * (g1 * b3 - g3 * b1));

a[3] = (a2 * b1 - a1 * b2 + (g1 * b2 - b1 * g2) * a[2]) / (b1 * z2 - z1 * b2);

a[4] = (a1 - z1 * a[3] - g1 * a[2]) / b1;

a[1] = (1 / (x2 - x0)) * (Math::Log(f(x2, p) / f(x0, p)) - a[4] * (x2 * x2 * x2

* x2 - x0 * x0 * x0 * x0) - a[3] * (x2 * x2 * x2 - x0 * x0 * x0)

- a[2] * (x2 * x2 - x0 * x0));

a[0] = f(x0, p) * Math::Exp(-(a[1] * x0 + a[2] * x0 * x0 + a[3] * x0 * x0 * x0 + a[4] * x0 * x0 * x0 * x0));

}

///////////////////////////////////////////////////////////////////////////

void ermit_4(double *a, double x0, double x2, int p) {

double a1, a2, a3, b1, b2, b3, z1, z2, z3, g1, g2, g3;

double x1, h;

x1 = (x0 + x2) / 2;

h = x1 - x0;

a1 = (f(x2, p) - f(x0, p)) / (x2 - x0) - (f(x1, p) - f(x0, p)) / (x1 - x0);

b1 = (x2 + x0) * (x2 * x2 + x0 * x0) - (x1 + x0) * (x1 * x1 + x0 * x0);

z1 = x2 * x2 + x2 * x0 - x1 * x1 - x1 * x0;

g1 = x2 - x1;

a2 = (f(x1, p) - f(x0, p)) / (x1 - x0) - fp(x0, p);

b2 = x1 * x1 * x1 + x0 * x1 * (x0 + x1) - 3* x0 * x0 * x0;

z2 = x1 * x1 + x0 * x1 - 2* x0 * x0;

g2 = x1 - x0;

a3 = (f(x1, p) - f(x0, p)) / (x1 - x0) - fp(x2, p);

b3 = (x0 + x1) * (x0 * x0 + x1 * x1) - 4* x2 * x2 * x2;

z3 = (x1 * x1 + x0 * x1 + x0 * x0) - 3* x2 * x2;

g3 = (x1 + x0 - 2* x2 );

a[2] = ((a2 * b1 - a1 * b2) * (z3 * b1 - z1 * b3) - (z2 * b1 - z1 * b2)

* (a3 * b1 - a1 * b3)) / ((g1 * b2 - g2 * b1) * (z1 * b3 - z3 * b1)

+ (z2 * b1 - z1 * b2) * (g1 * b3 - g3 * b1));

a[3] = (a2 * b1 - a1 * b2 + (g1 * b2 - b1 * g2) * a[2]) / (b1 * z2 - z1

* b2);

a[4] = (a1 - z1 * a[3] - g1 * a[2]) / b1;

a[1] = (f(x1, p) - f(x0, p)) / h - a[2] * (x1 + x0) - a[3] * (x1 * x1 + x1

* x0 + x0 * x0) - a[4] * (x1 + x0) * (x1 * x1 + x0 * x0);

a[0] = f(x0, p) - a[1] * x0 - a[2] * x0 * x0 - a[3] * x0 * x0 * x0 - a[4]

* x0 * x0 * x0 * x0;

}

////////////////////////////////////////////////////////////////

void ermit_5(double *a, double zl, double zp, int p) {

double h, x1;

h = (zp - zl) / 2;

x1 = (zp + zl) / 2;

a[3] = ((h * h * (fp(zp, p) - fp(zl, p))) / (f(zp, p) - f(zl, p) - h * (fp(

zp, p) + fp(zl, p)))) - x1;

a[2] = ((fp(zp, p) - fp(zl, p)) * (((x1 + a[3]) * (x1 + a[3]) - h * h)

* ((x1 + a[3]) * (x1 + a[3]) - h * h))) / (4* h * (x1 + a[3]));

a[0] = fp(zl, p) + a[2] / ((x1 + a[3] - h) * (x1 + a[3] - h));

a[1] = f(zl, p) - a[0] * (x1 - h) - a[2] / (x1 - h + a[3]);

}

////////////////////////////////////////////////////////////////////

void ermit_8(double *a, double zl, double zp, int p) {

double j0, j1, j2, m0, m1;

j0 = (Math::Exp(f(zp, p)) - Math::Exp(f(zl, p))) / (zp - zl);

j1 = (zl * zl - zp * zp) / (zp - zl);

j2 = (zl * zl * zl - zp * zp * zp) / (zp - zl);

m0 = (f(zl, p) * Math::Exp(f(zl, p)) - j0) / (j1 - 2* zl );

m1 = (2* zl * zl - j2) / (j1 - 2* zl );

a[3] = (-fp(zp, p) * Math::Exp(f(zp, p)) + j0 + m0 * j1 - 2* zp * m0) / (3* zp

* zp + 2* zp * m1 - j2 - m1 * j1);

a[2] = m0 + a[3] * m1;

a[1] = j0 + j1 * a[2] + a[3] * j2;

a[0] = Math::Exp(f(zl, p)) - a[1] * zl - a[2] * zl * zl - a[3] * zl * zl * zl;

}

///////////////////////////////////////////////////////////////////

void ermit_9(double *a, double zl, double zp, int p) {

double j1, j2, j3, j4, m1, m2, m3, k1, k2, z;

z = (zp + zl) / 2;

j1 = (zp * zp - z * z) / (z - zp);

j2 = (zp * zp * zp - z * z * z) / (z - zp);

j3 = (zp * zp * zp * zp - z * z * z * z) / (z - zp);

j4 = (Math::Exp(f(z, p)) - Math::Exp(f(zp, p))) / (z - zp);

m1 = (Math::Exp(f(zp, p)) - Math::Exp(f(zl, p)) + j4 * (zl - zp)) / (zp * zp - zl * zl + j1 * (zp - zl));

m2 = (zl * zl * zl - zp * zp * zp + j2 * (zl - zp)) / (zp * zp - zl * zl

+ j1 * (zp - zl));

m3 = (zl * zl * zl * zl - zp * zp * zp * zp + j3 * (zl - zp)) / (zp * zp

- zl * zl + j1 * (zp - zl));

k1 = (Math::Exp(f(zl, p)) * fp(zl, p) - j4 - m1 * j1 - 2* zl * m1) / (j2 + 3* zl

* zl + j1 * m2 + 2* m2 * zl);

k2 = (j3 + 4* zl * zl * zl + j1 * m3 + 2* m3 * zl) / (j2 + 3* zl * zl + j1

* m2 + 2* m2 * zl);

a[4] = (Math::Exp(f(zp, p)) * fp(zp, p) - j4 - m1 - j1 - 2* zp * m1 - k1 * j2

- 3* zp * zp * k1 - k1 * j1 * m2 - 2* m2 * zp * k1) / (j3 + 4* zp

* zp * zp + j1 * m3 + 2* m3 * zp - k2 * j2 - 3* zp * zp * k2 - k2

* j1 * m2 - 2* m2 * zp * k2);

a[3] = k1 - k2 * a[4];

a[2] = m1 + a[3] * m2 + a[4] * m3;

a[1] = j4 + a[2] * j1 + a[3] * j2 + a[4] * j3;

a[0] = Math::Exp(f(zl, p)) - a[1] * zl - a[2] * zl * zl - a[3] * zl * zl * zl

- a[4] * zl * zl * zl * zl;

}

///////////////////////////////////////////////////////////////////

double poldiv_p3(double*a, double zl, double b1, int n, int p) {

double zp, ny, x, nyu,ny1,ny2, x1, x2;

textBox2->Text="";

nyu=Double::Parse(textBox1->Text);

String ^ path = Path::GetFileName("rez.txt");

FileInfo^ fi = gcnew FileInfo(path);

StreamWriter ^ sw = fi->CreateText();

int l = 0;

double t,ch1,ch2,ch3;

chart1->Series["Function"]->Points->Clear();

chart1->Series["Spline"]->Points->Clear();

chart2->Series["error"]->Points->Clear();

zp = zl + 0.00510101101;;

while (1) {

do {

zp += 0.000135110101101;

if (zp > b1) {

zp = b1;

if (s1->Checked == true) {

ermit_1(a, zl, zp, p);

}

if (s2->Checked == true) {

ermit_2(a, zl, zp, p);

}

if (s3->Checked == true) {

ermit_3(a, zl, zp, p);

}

if (s4->Checked == true) {

ermit_4(a, zl, zp, p);

}

if (s5->Checked == true) {

ermit_5(a, zl, zp, p);

}

if (s6->Checked == true) {

ermit_6(a, zl, zp, p);

}

if (s7->Checked == true) {

ermit_8(a, zl, zp, p);

}

if (s8->Checked == true) {

ermit_9(a, zl, zp, p);

}

if (s9->Checked == true) {

ermit_7(a, zl, zp, p);

}

if(p==1){

x = (zl + zp) / 2;

}

if(p==2){

x1 = zl+(zp - zl) / 4;

x2 = zl+2.5*(zp - zl) / 4;

ny1=epx_p(a, x1, p);

ny2=epx_p(a, x2, p);

if(ny2>ny1){

x=x2;

}

else{x=x1;}

}

l++;

//fprint(a, zl, zp, n, ny, l);

//print(a, zl, zp, n, ny, l);

sw->WriteLine("{0:D} - ланка \n",l);

sw->WriteLine("a[0] = {0,7:e}\n", a[0]);

sw->WriteLine("a[1] = {0,7:e}\n", a[1]);

sw->WriteLine("a[2] = {0,7:e}\n", a[2]);

sw->WriteLine("a[3] = {0,7:e}\n", a[3]);

if (n == 5) {

sw->WriteLine("a[4] = {0,7:e}\n", a[4]);

}

sw->WriteLine("Ліва межа інтервалу = {0,7:e}\n", zl);

sw->WriteLine("Права межа інтервалу = {0,7:e}\n", zp);

sw->WriteLine("Похибка = {0,7:e}\n", ny);

sw->Write(sw->NewLine);

sw->Close();

for(t = zl; t <= zp; t += 0.01)

{

ch1 = f(t,p);

ch2 = sp(a,t);

ch3 = epx_p(a,t,1);

if(nyu=0.001){

if(ch3>nyu-0.00008){ch3-=0.000015;}

}

chart1->Series["Function"]->Points->AddXY(t, ch1);

chart1->Series["Spline"]->Points->AddXY(t, ch2);

chart2->Series["error"]->Points->AddXY(t, ch3);

}

return zp;

}// po if(zp > b1)

//z = (zp + ozp) / 2;

if (s1->Checked == true) {

ermit_1(a, zl, zp, p);

}

if (s2->Checked == true) {

ermit_2(a, zl, zp, p);

}

if (s3->Checked == true) {

ermit_3(a, zl, zp, p);

}

if (s4->Checked == true) {

ermit_4(a, zl, zp, p);

}

if (s5->Checked == true) {

ermit_5(a, zl, zp, p);

}

if (s6->Checked == true) {

ermit_6(a, zl, zp, p);

}

if (s7->Checked == true) {

ermit_8(a, zl, zp, p);

}

if (s8->Checked == true) {

ermit_9(a, zl, zp, p);

}

if (s9->Checked == true) {

ermit_7(a, zl, zp, p);

}

if(p==1){

x = (zl + zp) / 2;

}

if(p==2){

x1 = zl+(zp - zl) / 4;

x2 = zl+3*(zp - zl) / 4;

ny1=epx_p(a, x1, p);

ny2=epx_p(a, x2, p);

if(ny2>ny1){

x=x2;

}

else{x=x1;}

}

ny = epx_p(a, x, p);

//std::cout << "\n" << ny << " - " << nyu << "\t" << ny - nyu << "\n";

//ny=Math::Abs(f(x, p) - sp(a, x))/f(x,p)*100;

//nyu=(nyu/f(x,p))*100;

if(ny>nyu){

zp =zp- 0.000135110101101-(0.000135110101101)/2;

}

if (((nyu-ny)*100 < 0.0005)&&(nyu>ny)) {

break;

}

} while (1);

l++;

//fprint(a, zl, zp, n, ny, l);

//print(a, zl, zp, n, ny, l);

sw->WriteLine("{0:D} - ланка \n",l);

sw->WriteLine("a[0] = {0,7:e}\n", a[0]);

sw->WriteLine("a[1] = {0,7:e}\n", a[1]);

sw->WriteLine("a[2] = {0,7:e}\n", a[2]);

sw->WriteLine("a[3] = {0,7:e}\n", a[3]);

if (n == 5) {

sw->WriteLine("a[4] = {0,7:e}\n", a[4]);

}

sw->WriteLine("Ліва межа інтервалу = {0,7:e}\n", zl);

sw->WriteLine("Права межа інтервалу = {0,7:e}\n", zp);

sw->WriteLine("Похибка = {0,7:e}\n", ny);

sw->Write(sw->NewLine);

for(t = zl; t <= zp; t += 0.01)

{

ch1 = f(t,p);

ch2 = sp(a,t);

ch3 = epx_p(a,t,1);

if(nyu=0.001){

if(ch3>nyu-0.00008){ch3-=0.000015;}

}

chart1->Series["Function"]->Points->AddXY(t, ch1);

chart1->Series["Spline"]->Points->AddXY(t, ch2);

chart2->Series["error"]->Points->AddXY(t, ch3);

}

zl = zp;

zp += 0.000135110101101;

}

sw->Write(sw->NewLine);

sw->Close();

for(t = zl; t <= zp; t += 0.01)

{

ch1 = f(t,p);

ch2 = sp(a,t);

ch3 = epx_p(a,t,1);

if(nyu=0.001){

if(ch3>nyu-0.00008){ch3-=0.000015;}

}

chart1->Series["Function"]->Points->AddXY(t, ch1);

chart1->Series["Spline"]->Points->AddXY(t, ch2);

chart2->Series["error"]->Points->AddXY(t, ch3);

}

return zp;

}

//***************************************************************************void algo_p3(double*a, double zl, double b1, int n, int p) {

double X, Y, eps, nyu, x, x1, x0, zp, xx, zz,ny,dz;

nyu=Double::Parse(textBox1->Text);

String ^ path = Path::GetFileName("rez.txt");

FileInfo^ fi = gcnew FileInfo(path);

StreamWriter ^ sw = fi->CreateText();

int l = 0;

double t,ch1,ch2,ch3;

chart1->Series["Function"]->Points->Clear();

chart1->Series["Spline"]->Points->Clear();

chart2->Series["error"]->Points->Clear();

x0 = 0.1;

//zz = zp =

x1 = 0.5;

//xx =

x = 0.3;

eps = 0.00001;

nyu = 0.001;

int j = 0;

do {

Y = (f2dx(x, x1, x0, p) * ff1(x, x1, x0, p) - ff2(x, x1, x0, nyu, p)

* f1dx(x, x1, x0, p)) / (f2dy(x, x1, x0, p)

* f1dx(x, x1, x0, p) - f2dx(x, x1, x0, p) * f1dy(x, x1, x0, p));

X = (-ff1(x, x1, x0, p) - f1dy(x, x1, x0, p) * Y) / f1dx(x, x1, x0, p);

x += X;

x1 += Y;

} while ((Math::Abs(ff1(x, x1, x0, p)) >= eps) && (Math::Abs(ff2(x, x1, x0, nyu, p)) >= eps));

sw->WriteLine("{0:D} - ланка \n",l);

sw->WriteLine("a[0] = {0,7:e}\n", a[0]);

sw->WriteLine("a[1] = {0,7:e}\n", a[1]);

sw->WriteLine("a[2] = {0,7:e}\n", a[2]);

sw->WriteLine("a[3] = {0,7:e}\n", a[3]);

if (n == 5) {

sw->WriteLine("a[4] = {0,7:e}\n", a[4]);

}

sw->WriteLine("Ліва межа інтервалу = {0,7:e}\n", zl);

sw->WriteLine("Права межа інтервалу = {0,7:e}\n", zp);

sw->WriteLine("Похибка = {0,7:e}\n", ny);

sw->Write(sw->NewLine);

for(t = zl; t <= zp; t += 0.01)

{

ch1 = f(t,p);

ch2 = sp(a,t);

ch3 = epx_p(a,t,1);

chart1->Series["Function"]->Points->AddXY(t, ch1);

chart1->Series["Spline"]->Points->AddXY(t, ch2);

chart2->Series["error"]->Points->AddXY(t, ch3);

}

zl = zp;

zp += dz;}

Результати роботи програми

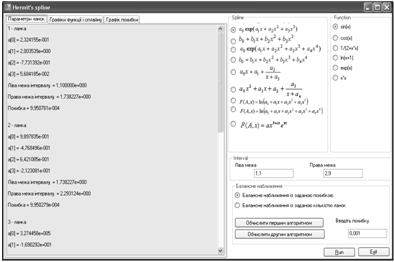
Рис. 1. Параметри ланок сплайна

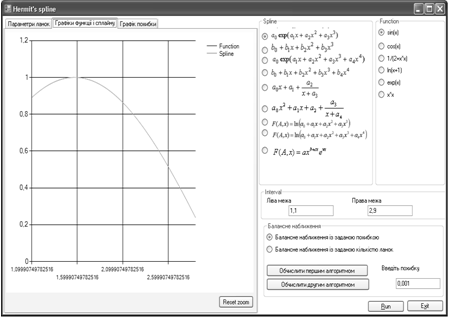
Рис. 2. Графік сплайна і функції .

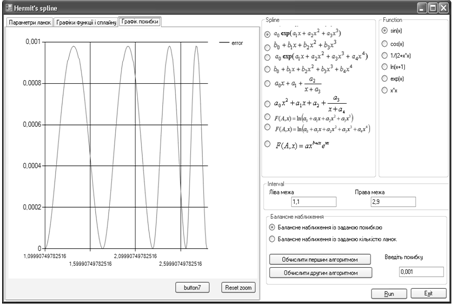
Рис. 3. Графік похибки наближення функції