Шпаргалка: Формулы (математический анализ)

Шпаргалка: Формулы (математический анализ)

шпаргалка

Формулы дифференцирования                       Таблица основных интегралов

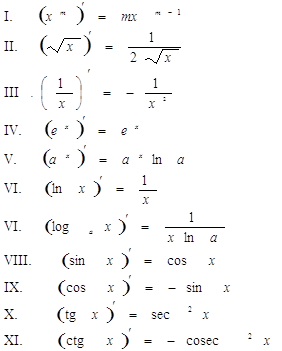
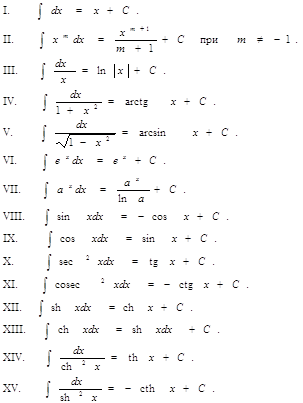
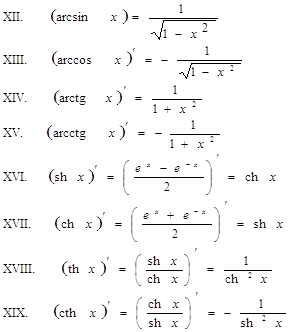
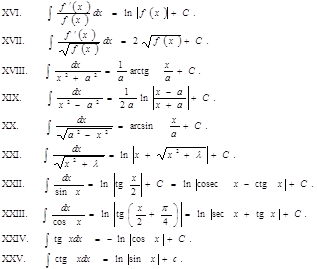
Правила интегрирования

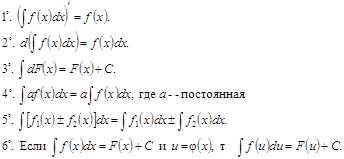
Основные правила дифференцирования

Пусть С—постоянная, u=u(x), v=v(x) – функции, имеющие

производные.

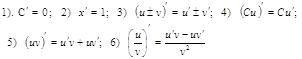
7)

Интегрирование по частям                                       

Основные свойства определённого интеграла

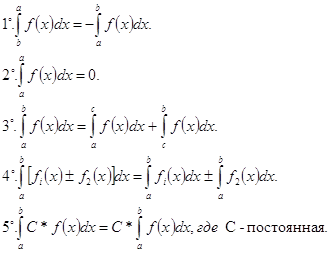
Интегрирование простейших дробей

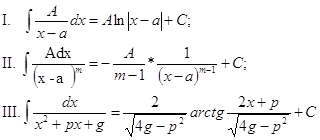
Замена переменной в  неопределенном интеграле

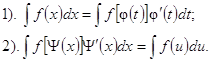
Площадь плоской фигуры

Площадь криволинейной трапеции, ограниченной кривой , прямыми и отрезком[a, b] оси Ox, вычисляется по формуле

Площадь фигуры, ограниченной кривыми и прямыми , находится по формуле

Если кривая задана параметрическими уравнениями , то площадь криволинейной трапеции, ограниченной этой кривой, прямыми и отрезком[a, b] оси Ox, выражается формулой

где определяются из уравнений

Площадь криволинейного сектора, ограниченного кривой, заданной в полярных координатах уравнением и двумя полярными радиусами находится по формуле

Длина дуги плоской кривой

Если кривая y=f(x) на отрезке [a, b] – гладкая (т.е. производная непрерывна), то длина соответствующей дуги этой кривой находится по формуле

При параметрическом задании кривой x=x(t),  y=y(t) [x(t) и y(t) – непрерывно дифференцируемые функции] длина дуги кривой, соответствующая монотонному изменению параметра , вычисляется по формуле

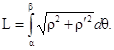Если гладкая кривая задана в полярных координатах уравнением , то длина дуги равна

Вычисление объема тела

Вычисление объема тела по известным площадям поперечных сечений.

Если площадь сечения тела плоскостью, перпендикулярной оси Ox, может быть выражена как функция от x, т.е. в виде , то объем части тела, заключенной между перпендикулярными оси Ox плоскостями x=a и x=b, находится по формуле

Вычисление объема тела вращения. Если криволинейная трапеция, ограниченная кривой и прямыми вращается вокруг оси Ox, то объем тела вращения вычисляется по формуле

Если фигура, ограниченная кривыми и прямыми x=a, x=b, вращается вокруг оси Ox, то объем тела вращения

Вычисление площади поверхности вращения

Если дуга гладкой кривой вращается вокруг оси Ox, то площадь поверхности вращения вычисляется по формуле

Если кривая задана параметрическими уравнениями , то

Список литературы

Для подготовки данной работы были использованы материалы с сайта http://www.shpori4all. narod.ru/