
Рефераты по авиации и космонавтике
Рефераты по административному праву
Рефераты по безопасности жизнедеятельности
Рефераты по арбитражному процессу
Рефераты по архитектуре
Рефераты по астрономии
Рефераты по банковскому делу
Рефераты по сексологии
Рефераты по информатике программированию
Рефераты по биологии
Рефераты по экономике
Рефераты по москвоведению
Рефераты по экологии
Краткое содержание произведений
Рефераты по физкультуре и спорту
Топики по английскому языку
Рефераты по математике
Рефераты по музыке
Остальные рефераты
Рефераты по биржевому делу
Рефераты по ботанике и сельскому хозяйству
Рефераты по бухгалтерскому учету и аудиту
Рефераты по валютным отношениям
Рефераты по ветеринарии
Рефераты для военной кафедры
Рефераты по географии
Рефераты по геодезии
Рефераты по геологии
Рефераты по геополитике
Рефераты по государству и праву
Рефераты по гражданскому праву и процессу
Рефераты по кредитованию
Рефераты по естествознанию
Рефераты по истории техники
Рефераты по журналистике
Рефераты по зоологии
Рефераты по инвестициям
Рефераты по информатике
Исторические личности
Рефераты по кибернетике
Рефераты по коммуникации и связи
Рефераты по косметологии
Рефераты по криминалистике
Рефераты по криминологии
Рефераты по науке и технике
Рефераты по кулинарии
Рефераты по культурологии
Учебное пособие: Определенный интеграл
Учебное пособие: Определенный интеграл
Определенный интеграл
Содержание
Лекция 1. Определенный интеграл
1. Понятие определенного интеграла
2. Геометрический смысл определенного интеграла
3. Основные свойства определенного интеграла
4. Формула Ньютона–Лейбница
5. Замена переменной в определенном интеграле
6. Интегрирование по частям
Лекция 2. Применение определенных интегралов. несобственные интегралы
1. Площадь криволинейной трапеции
2. Объем тела вращения
3. Длина дуги плоской кривой
4. Несобственные интегралы с бесконечными пределами интегрирования
5. Несобственные интегралы от неограниченных функций
Литература
Лекция 1. Определенный интеграл
1. Понятие определенного интеграла
Пусть функция
![]() определена на отрезке
определена на отрезке ![]() ,
, ![]() . Выполним следующие
операции:
. Выполним следующие
операции:
1) разобьем отрезок ![]() точками
точками ![]() на n частичных отрезков
на n частичных отрезков ![]() ;
;
2) в каждом из частичных
отрезков ![]() ,
, ![]() выберем произвольную точку
выберем произвольную точку
![]() и вычислим значение
функции в этой точке:
и вычислим значение
функции в этой точке: ![]() ;
;
3) найдем произведения ![]() , где
, где ![]() – длина частичного отрезка
– длина частичного отрезка
![]() ,
, ![]() ;
;
4) составим сумму
 , (1)
, (1)
которая
называется интегральной суммой функции y = f(x) на отрезке [а, b]. С геометрической точки
зрения интегральная сумма ![]() представляет
собой сумму площадей прямоугольников, основаниями которых являются частичные
отрезки
представляет
собой сумму площадей прямоугольников, основаниями которых являются частичные
отрезки ![]() , а высоты равны
, а высоты равны ![]() соответственно (рис. 1).
Обозначим через
соответственно (рис. 1).
Обозначим через ![]() длину
наибольшего частичного отрезка
длину
наибольшего частичного отрезка ![]() ;
;
5) найдем предел
интегральной суммы, когда ![]() .
.
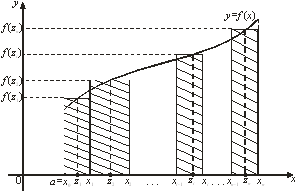
Рис. 1
Определение. Если существует конечный
предел интегральной суммы (1) и он не зависит ни от способа разбиения отрезка ![]() на частичные отрезки, ни
от выбора точек
на частичные отрезки, ни
от выбора точек ![]() в них, то этот
предел называется определенным интегралом от функции
в них, то этот
предел называется определенным интегралом от функции ![]() на отрезке
на отрезке ![]() и обозначается
и обозначается 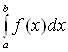 .
.
Таким
образом, 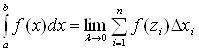 .
.
В этом случае
функция ![]() называется интегрируемой
на
называется интегрируемой
на ![]() . Числа а и b называются
соответственно нижним и верхним пределами интегрирования,
. Числа а и b называются
соответственно нижним и верхним пределами интегрирования, ![]() – подынтегральной
функцией,
– подынтегральной
функцией, ![]() – подынтегральным
выражением,
– подынтегральным
выражением, ![]() – переменной
интегрирования; отрезок
– переменной
интегрирования; отрезок ![]() называется
промежутком интегрирования.
называется
промежутком интегрирования.
Теорема 1.
Если
функция ![]() непрерывна на отрезке
непрерывна на отрезке ![]() , то она интегрируема на
этом отрезке.
, то она интегрируема на
этом отрезке.
2. Геометрический смысл определенного интеграла
Пусть на
отрезке ![]() задана непрерывная
неотрицательная функция
задана непрерывная
неотрицательная функция ![]() . Криволинейной
трапецией называется фигура, ограниченная сверху графиком функции y = f(x), снизу – осью Ох, слева
и справа – прямыми x = a и x = b (рис. 2).
. Криволинейной
трапецией называется фигура, ограниченная сверху графиком функции y = f(x), снизу – осью Ох, слева
и справа – прямыми x = a и x = b (рис. 2).
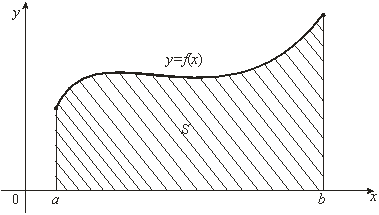
Рис. 2
Определенный
интеграл  от неотрицательной функции
от неотрицательной функции
![]() с геометрической точки
зрения численно равен площади криволинейной трапеции, ограниченной сверху
графиком функции
с геометрической точки
зрения численно равен площади криволинейной трапеции, ограниченной сверху
графиком функции ![]() , слева и справа
– отрезками прямых
, слева и справа
– отрезками прямых ![]() и
и ![]() , снизу – отрезком
, снизу – отрезком ![]() оси Ох.
оси Ох.
3. Основные свойства определенного интеграла
1. Значение определенного
интеграла не зависит от обозначения переменной интегрирования: 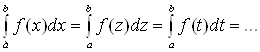 .
.
2. Определенный интеграл с
одинаковыми пределами интегрирования равен нулю: 
3. Если ![]() , то, по определению,
полагаем
, то, по определению,
полагаем 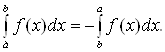
4. Постоянный множитель
можно выносить за знак определенного интеграла: 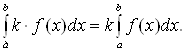
5. Определенный интеграл от алгебраической суммы двух функций равен алгебраической сумме определенных интегралов от этих функций:
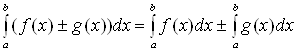 .
.
6. Если функция ![]() интегрируема на
интегрируема на ![]() и
и ![]() , то
, то
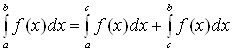 .
.
7. (теорема о среднем).
Если функция ![]() непрерывна на отрезке
непрерывна на отрезке ![]() , то на этом отрезке
существует точка
, то на этом отрезке
существует точка ![]() , такая, что
, такая, что 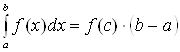 .
.
4. Формула Ньютона–Лейбница
Вычисление определенных интегралов через предел интегральных сумм связано с большими трудностями. Поэтому существует другой метод, основанный на тесной связи, существующей между понятиями определенного и неопределенного интегралов.
Теорема 2.
Если
функция ![]() непрерывна на отрезке
непрерывна на отрезке ![]() и
и ![]() – какая-либо ее
первообразная на этом отрезке, то справедлива следующая формула:
– какая-либо ее
первообразная на этом отрезке, то справедлива следующая формула:
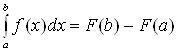 , (2)
, (2)
которая
называется формулой Ньютона–Лейбница. Разность ![]() принято записывать
следующим образом:
принято записывать
следующим образом:
![]() ,
,
где символ![]() называется знаком двойной
подстановки.
называется знаком двойной
подстановки.
Таким образом, формулу (2) можно записать в виде:
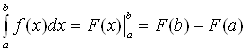 .
.
Нахождение
определенных интегралов с помощью формулы Ньютона-Лейбница осуществляется в два
этапа: на первом этапе находят некоторую первообразную ![]() для подынтегральной
функции
для подынтегральной
функции ![]() ; на втором – находится
разность
; на втором – находится
разность ![]() значений этой
первообразной на концах отрезка
значений этой
первообразной на концах отрезка ![]() .
.
Пример 1. Вычислить интеграл ![]() .
.
Решение. Для
подынтегральной функции ![]() произвольная
первообразная имеет вид
произвольная
первообразная имеет вид ![]() . Так
как в формуле Ньютона-Лейбни-ца можно использовать любую первообразную, то для
вычисления ин-
. Так
как в формуле Ньютона-Лейбни-ца можно использовать любую первообразную, то для
вычисления ин-
теграла возьмем первообразную, имеющую наиболее простой вид: ![]() . Тогда
. Тогда 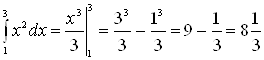 .
.
Пример 2. Вычислить интеграл 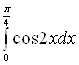 .
.
Решение. По формуле Ньютона-Лейбница имеем:
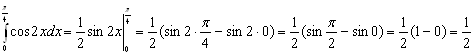 .
.
5. Замена переменной в определенном интеграле
Теорема 3. Пусть функция ![]() непрерывна на отрезке
непрерывна на отрезке ![]() . Тогда, если: 1) функция
. Тогда, если: 1) функция ![]() и ее производная
и ее производная ![]() непрерывны при
непрерывны при ![]() ; 2) множеством значений
функции
; 2) множеством значений
функции ![]() при
при ![]() является отрезок
является отрезок ![]() ; 3)
; 3) ![]() ,
, ![]() , то справедлива формула
, то справедлива формула
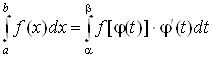 , (3)
, (3)
которая называется формулой замены переменной в определенном интеграле.
Заметим, что
как и в случае неопределенного интеграла, использование замены переменной
позволяет упростить исходный интеграл, приблизив его к табличному. При этом в
отличие от неопределенного интеграла в данном случае нет необходимости
возвращаться к исходной переменной интегрирования – достаточно лишь найти новые
пределы интегрирования ![]() и
и ![]() (для этого надо решить
относительно переменной t уравнения
(для этого надо решить
относительно переменной t уравнения ![]() и
и ![]() )).
)).
На практике
часто вместо подстановки ![]() используют
подстановку
используют
подстановку ![]() . В этом случае нахождение
новых пределов интегрирования по переменной t упрощается:
. В этом случае нахождение
новых пределов интегрирования по переменной t упрощается: ![]() ,
, ![]() .
.
Пример 3. Вычислить интеграл 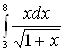
Решение. Введем
новую переменную по формуле ![]() . Определим
. Определим
![]() и
и ![]() . Возведя в квадрат обе
части равенства
. Возведя в квадрат обе
части равенства ![]() , получим
, получим ![]() , откуда
, откуда ![]()
![]() . Находим новые пределы
интегрирования. Для этого в формулу
. Находим новые пределы
интегрирования. Для этого в формулу![]() подставим
старые пределы
подставим
старые пределы ![]() и
и ![]() . Получим:
. Получим: ![]() , откуда
, откуда ![]() и, следовательно,
и, следовательно, ![]() ;
; ![]() , откуда
, откуда ![]() и, следовательно,
и, следовательно, ![]() . Таким образом:
. Таким образом:
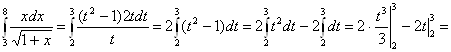
![]() .
.
Пример 4. Вычислить интеграл 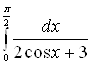 .
.
Решение. Воспользуемся
универсальной тригонометрической подстановкой. Положим ![]() , откуда
, откуда ![]()
![]() ,
, ![]() . Найдем новые пределы
интегрирования: если
. Найдем новые пределы
интегрирования: если ![]() , то
, то ![]() ; если
; если ![]() , то
, то ![]() . Значит,
. Значит, ![]() . Следовательно:
. Следовательно:
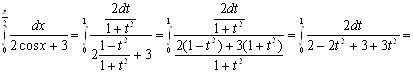
![]()
![]() .
.
Пример 5. Вычислить интеграл 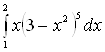 .
.
Решение.
Положим ![]() , тогда
, тогда ![]() , откуда
, откуда ![]() . Находим новые пределы
интегрирования:
. Находим новые пределы
интегрирования: ![]() ;
; ![]() . Имеем:
. Имеем: ![]() . Следовательно:
. Следовательно:
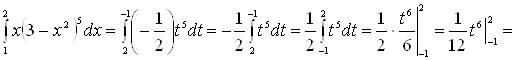
![]() .
.
6. Интегрирование по частям
Теорема 4. Пусть функции ![]() и
и ![]() имеют непрерывные
производные на отрезке
имеют непрерывные
производные на отрезке ![]() . Тогда имеет
место следующая формула интегрирования по частям:
. Тогда имеет
место следующая формула интегрирования по частям:
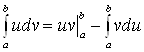 . (4)
. (4)
Доказательство
Так как ![]() , то функция
, то функция ![]() является первообразной для
функции
является первообразной для
функции ![]() . Тогда по формуле
Ньютона–Лейбница получаем
. Тогда по формуле
Ньютона–Лейбница получаем
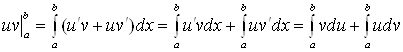 ,
,
откуда
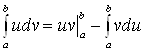 .
.
Пример 6. Вычислить  .
.
Решение.
Положим ![]() , отсюда
, отсюда ![]() . По формуле (4) находим
. По формуле (4) находим
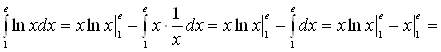
![]() .
.
Пример 7. Вычислить 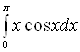 .
.
Решение.
Пусть ![]() , тогда
, тогда ![]() . Применяя формулу
интегрирования по частям, получаем
. Применяя формулу
интегрирования по частям, получаем

![]() .
.
Пример 8. Вычислить 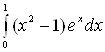 .
.
Решение.
Полагая ![]() , определяем
, определяем ![]() . Следовательно:
. Следовательно:
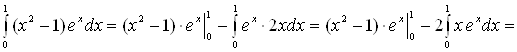
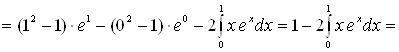 [к полученному интегра-лу снова применяем
формулу интегрирования по частям:
[к полученному интегра-лу снова применяем
формулу интегрирования по частям: ![]() ;
следовательно:
;
следовательно: ![]() ] =
] = ![]() =
= ![]()
![]() .
.
Лекция 2. Применение определенных интегралов. Несобственные интегралы
1. Площадь криволинейной трапеции
Пусть функция
![]() неотрицательна и
непрерывна на отрезке
неотрицательна и
непрерывна на отрезке ![]() . Тогда, согласно
геометрическому смыслу определенного интеграла, площадь криволинейной трапеции,
ограниченной сверху графиком этой функции, снизу – осью
. Тогда, согласно
геометрическому смыслу определенного интеграла, площадь криволинейной трапеции,
ограниченной сверху графиком этой функции, снизу – осью ![]() , слева и справа – прямыми
, слева и справа – прямыми ![]() и
и ![]() (см. рис. 2)
вычисляется по формуле
(см. рис. 2)
вычисляется по формуле
 . (5)
. (5)
Пример 9. Найти площадь фигуры,
ограниченной линией ![]() и осью
и осью ![]() .
.
Решение.
Графиком функции ![]() является
парабола, ветви которой направлены вниз. Построим ее (рис. 3). Чтобы
определить пределы интегрирования, найдем точки пересечения линии (параболы) с
осью
является
парабола, ветви которой направлены вниз. Построим ее (рис. 3). Чтобы
определить пределы интегрирования, найдем точки пересечения линии (параболы) с
осью ![]() (прямой
(прямой ![]() ). Для этого решаем систему
уравнений
). Для этого решаем систему
уравнений
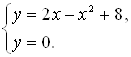
Получаем: ![]() , откуда
, откуда ![]() ,
, ![]() ; следовательно,
; следовательно, ![]() ,
, ![]() .
.
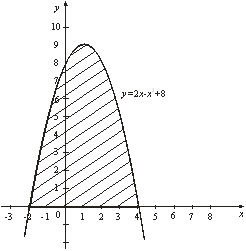
Рис. 3
Площадь фигуры находим по формуле (5):
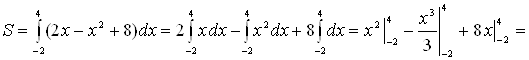
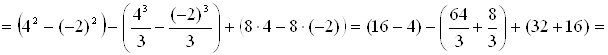
![]() (кв. ед.).
(кв. ед.).
Если функция ![]() неположительна и
непрерывна на отрезке
неположительна и
непрерывна на отрезке ![]() , то площадь
криволинейной трапеции, ограниченной снизу графиком данной функции, сверху –
осью
, то площадь
криволинейной трапеции, ограниченной снизу графиком данной функции, сверху –
осью ![]() , слева и справа – прямыми
, слева и справа – прямыми ![]() и
и ![]() , вычисляется по формуле
, вычисляется по формуле
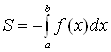 . (6)
. (6)
В случае если
функция ![]() непрерывна на отрезке
непрерывна на отрезке ![]() и меняет знак в конечном
числе точек, то площадь заштрихованной фигуры (рис. 4) равна
алгебраической сумме соответствующих определенных интегралов:
и меняет знак в конечном
числе точек, то площадь заштрихованной фигуры (рис. 4) равна
алгебраической сумме соответствующих определенных интегралов:
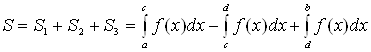 . (7)
. (7)
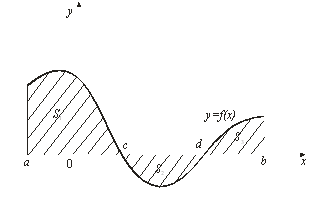
Рис. 4
Пример 10. Вычислить площадь
фигуры, ограниченной осью ![]() и
графиком функции
и
графиком функции ![]() при
при ![]() .
.

Рис. 5
Решение.
Сделаем чертеж (рис. 5). Искомая площадь представляет собой сумму площадей
![]() и
и ![]() . Найдем каждую из этих
площадей. Вначале определим пределы интегрирования, решив систему
. Найдем каждую из этих
площадей. Вначале определим пределы интегрирования, решив систему 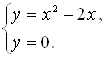 Получим
Получим ![]() ,
, ![]() . Следовательно:
. Следовательно:
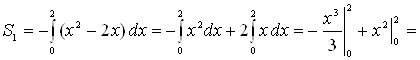
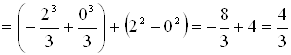 ;
;
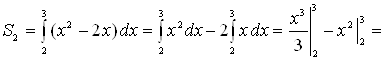
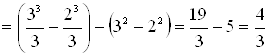 .
.
Таким
образом, площадь ![]() заштрихованной
фигуры равна
заштрихованной
фигуры равна
![]() (кв. ед.).
(кв. ед.).
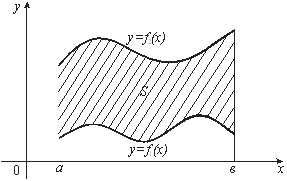
Рис. 6
Пусть,
наконец, криволинейная трапеция ограничена сверху и снизу графиками непрерывных
на отрезке ![]() функций
функций ![]() и
и ![]() ,
,
а слева и справа – прямыми ![]() и
и ![]() (рис. 6). Тогда ее
площадь вычисляется по формуле
(рис. 6). Тогда ее
площадь вычисляется по формуле
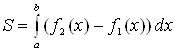 . (8)
. (8)
Пример 11. Найти площадь фигуры,
ограниченной линиями ![]() и
и ![]() .
.
Решение.
Данная фигура изображена на рис. 7. Площадь ее вычислим по формуле (8).
Решая систему уравнений  находим
находим
![]() ,
, ![]() ; следовательно,
; следовательно, ![]() ,
, ![]() . На отрезке
. На отрезке ![]() имеем:
имеем: ![]() . Значит, в формуле (8) в
качестве
. Значит, в формуле (8) в
качестве ![]() возьмем x, а в качестве
возьмем x, а в качестве ![]() –
– ![]() . Получим:
. Получим:
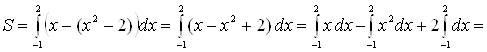
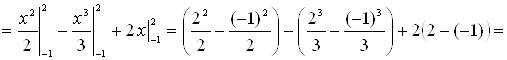
![]() (кв. ед.).
(кв. ед.).
Более сложные задачи на вычисление площадей решают путем разбиения фигуры на непересекающиеся части и вычисления площади всей фигуры как суммы площадей этих частей.
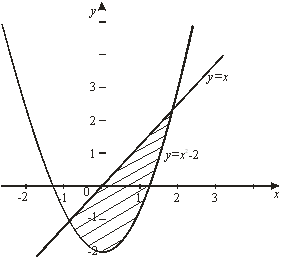
Рис. 7
Пример 12. Найти площадь фигуры,
ограниченной линиями ![]() ,
, ![]()
![]() ,
, ![]() .
.
Решение.
Сделаем чертеж (рис. 8). Данную фигуру можно рассматривать как
криволинейную трапецию, ограниченную снизу осью ![]() ,
слева и справа – прямыми
,
слева и справа – прямыми ![]() и
и ![]() , сверху – графиками
функций
, сверху – графиками
функций ![]() и
и ![]() . Так как фигура ограничена
сверху графиками двух функций, то для вычисления ее площади разобьем данную
фигуру прямой
. Так как фигура ограничена
сверху графиками двух функций, то для вычисления ее площади разобьем данную
фигуру прямой ![]() на две части (1
– это абсцисса точки пересечения линий
на две части (1
– это абсцисса точки пересечения линий ![]() и
и
![]() ). Площадь каждой из этих
частей находим по формуле (4):
). Площадь каждой из этих
частей находим по формуле (4):
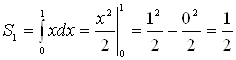 (кв. ед.);
(кв. ед.);  (кв. ед.). Следовательно:
(кв. ед.). Следовательно:
![]() (кв. ед.).
(кв. ед.).

Рис. 8
|
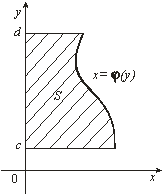
Рис. 9
В заключение
отметим, что если криволинейная трапеция ограничена прямыми ![]() и
и ![]() , осью
, осью ![]() и непрерывной на
и непрерывной на ![]() кривой
кривой ![]() (рис. 9), то ее
площадь находится по формуле
(рис. 9), то ее
площадь находится по формуле
 .
.
2. Объем тела вращения
Пусть
криволинейная трапеция, ограниченная графиком непрерывной на отрезке ![]() функции
функции ![]() , осью
, осью ![]() , прямыми
, прямыми ![]() и
и ![]() , вращается вокруг оси
, вращается вокруг оси ![]() (рис. 10). Тогда объем
полученного тела вращения вычисляется по формуле
(рис. 10). Тогда объем
полученного тела вращения вычисляется по формуле
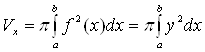 . (9)
. (9)
Пример 13. Вычислить объем тела,
полученного вращением вокруг оси ![]() криволинейной
трапеции, ограниченной гиперболой
криволинейной
трапеции, ограниченной гиперболой ![]() , прямыми
, прямыми
![]() ,
, ![]() и осью
и осью ![]() .
.
Решение. Сделаем чертеж (рис. 11).
Из условия
задачи следует, что ![]() ,
, ![]() . По формуле (9) получаем
. По формуле (9) получаем
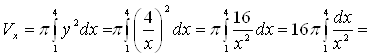
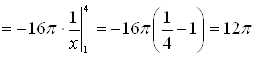 .
.
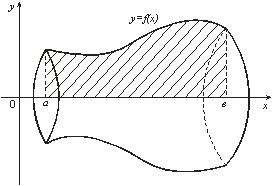
Рис. 10
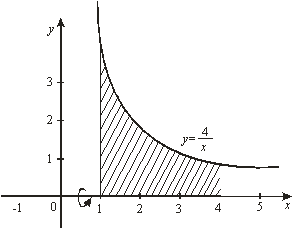
Рис. 11
Объем тела,
полученного вращением вокруг оси Оу криволинейной трапеции, ограниченной
прямыми у = с и у = d, осью Оу и графиком непрерывной на отрезке ![]() функции
функции ![]() (рис. 12),
определяется по формуле
(рис. 12),
определяется по формуле
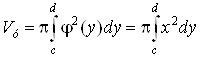 . (10)
. (10)
|
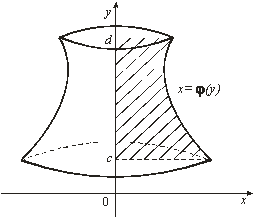
Рис. 12
Пример 14. Вычислить объем тела, полученного вращением вокруг оси Оу криволинейной трапеции, ограниченной линиями х2 = 4у, у = 4, х = 0 (рис. 13).
Решение. В
соответствии с условием задачи находим пределы интегрирования: ![]() ,
, ![]() . По формуле (10) получаем:
. По формуле (10) получаем:
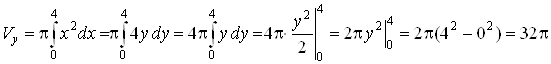 .
.

Рис. 13
3. Длина дуги плоской кривой
Пусть кривая ![]() , заданная уравнением
, заданная уравнением ![]() , где
, где ![]() , лежит в плоскости
, лежит в плоскости ![]() (рис. 14).
(рис. 14).
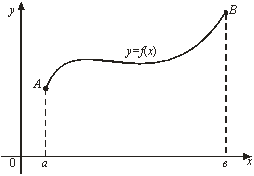
Рис. 14
Определение. Под длиной дуги ![]() понимается предел, к
которому стремится длина ломаной линии, вписанной в эту дугу, когда число
звеньев ломаной стремится к бесконечности, а длина наибольшего звена стремится
к нулю.
понимается предел, к
которому стремится длина ломаной линии, вписанной в эту дугу, когда число
звеньев ломаной стремится к бесконечности, а длина наибольшего звена стремится
к нулю.
Если функция ![]() и ее производная
и ее производная ![]() непрерывны на отрезке
непрерывны на отрезке ![]() , то длина дуги кривой
, то длина дуги кривой ![]() вычисляется по формуле
вычисляется по формуле
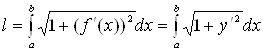 . (11)
. (11)
Пример 15. Вычислить длину дуги
кривой ![]() , заключенной между
точками, для которых
, заключенной между
точками, для которых ![]() .
.
Решение. Из
условия задачи имеем ![]() . По формуле (11)
получаем:
. По формуле (11)
получаем:
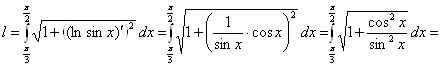
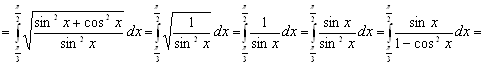
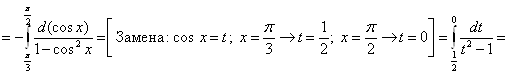
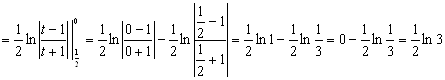 .
.
4. Несобственные интегралы с бесконечными пределами интегрирования
При введении
понятия определённого интеграла 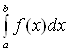 предполагалось,
что выполняются следующие два условия:
предполагалось,
что выполняются следующие два условия:
а) пределы
интегрирования а и ![]() являются
конечными;
являются
конечными;
б) подынтегральная
функция ![]() ограничена на отрезке
ограничена на отрезке ![]() .
.
Если хотя бы одно из этих условий не выполняется, то интеграл называется несобственным.
Рассмотрим вначале несобственные интегралы с бесконечными пределами интегрирования.
Определение. Пусть функция ![]() определена и непрерывна на
промежутке
определена и непрерывна на
промежутке ![]() , тогда
, тогда
 (12)
(12)
называется несобственным интегралом с бесконечным верхним пределом интегрирования (несобственным интегралом I рода).
Если 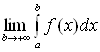 существует и конечен, то
несобственный интеграл
существует и конечен, то
несобственный интеграл 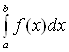 называется
сходящимся; если данный предел не существует или равен
называется
сходящимся; если данный предел не существует или равен ![]() , то несобственный интеграл
называется расходящимся.
, то несобственный интеграл
называется расходящимся.
Геометрически
несобственный интеграл 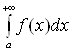 от
неотрицательной функции
от
неотрицательной функции ![]() выражает
площадь бесконечной криволинейной трапеции, ограниченной сверху графиком
функции
выражает
площадь бесконечной криволинейной трапеции, ограниченной сверху графиком
функции ![]() , снизу – осью
, снизу – осью ![]() , слева – отрезком прямой
, слева – отрезком прямой ![]() и неограниченной справа
(рис. 15).
и неограниченной справа
(рис. 15).
Если несобственный интеграл сходится, то эта площадь является конечной; если несобственный интеграл расходится, то эта площадь бесконечна.

Рис. 15
Аналогично определяется несобственный интеграл с бесконечным нижним пределом интегрирования:
 . (13)
. (13)
Этот интеграл сходится, если предел в правой части равенства (13) существует и конечен; в противном случае интеграл называется расходящимся.
Несобственный интеграл с двумя бесконечными пределами интегрирования определяется следующим образом:
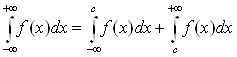 , (14)
, (14)
где с – любая
точка интервала ![]() . Интеграл
. Интеграл 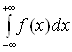 сходится только в том
случае, когда сходятся оба интеграла в правой части равенства (14).
сходится только в том
случае, когда сходятся оба интеграла в правой части равенства (14).
Пример 16. Исследовать на сходимость несобственные интегралы:
а) ![]() ; б)
; б)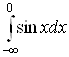 ; в)
; в) 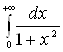 ; г)
; г)  .
.
Решение. а) 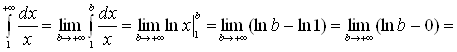
![]() , следовательно, данный интеграл расходится;
, следовательно, данный интеграл расходится;
б) 
![]() . Так как при
. Так как при ![]() предел
предел
![]() не существует, то интеграл
не существует, то интеграл
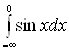 расходится;
расходится;
в) 
![]() Значит, несобственный интеграл
Значит, несобственный интеграл 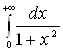 сходится и его значение
равно
сходится и его значение
равно ![]() ;
;
г)  = [выделим в знаменателе
полный квадрат:
= [выделим в знаменателе
полный квадрат: ![]() ] =
] = 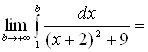 [замена:
[замена: ![]()
![]() ] =
] = 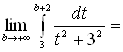

![]()
Значит,
несобственный интеграл сходится и его значение равно ![]() .
.
5. Несобственные интегралы от неограниченных функций
Пусть функция
![]() непрерывна на конечном
промежутке
непрерывна на конечном
промежутке ![]() , но не ограничена на этом
промежутке.
, но не ограничена на этом
промежутке.
Определение. Несобственным интегралом
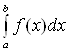 от функции у=f(x) на промежутке
от функции у=f(x) на промежутке ![]() называется предел
называется предел  , т.е.
, т.е.
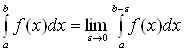 . (15)
. (15)
Если предел, стоящий в правой части равенства (15) существует и конечен, то несобственный интеграл называется сходящимся, в противном случае – расходящимся.
Интеграл (15) иногда называют несобственным интегралом второго рода.
Аналогично
вводится понятие несобственного интеграла от функции ![]() непрерывной, но не ограниченной
на промежутке
непрерывной, но не ограниченной
на промежутке ![]() :
:
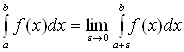 . (16)
. (16)
Если функция ![]() не ограничена при
не ограничена при ![]() , где
, где ![]() , и непрерывна при
, и непрерывна при ![]() и
и ![]() , то несобственный интеграл
от функции у=f(x) на отрезке
, то несобственный интеграл
от функции у=f(x) на отрезке ![]() обозначается
обозначается 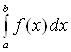 и определяется равенством
и определяется равенством
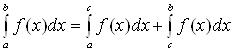 . (17)
. (17)
Несобственный
интеграл (17) называется сходящимся, если сходятся оба несобственных интеграла
в правой части равенства (17).
В противном случае данный интеграл называется расходящимся.
Пример 17. Исследовать на сходимость несобственные интегралы:
а) 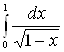 ; б)
; б)  .
.
Решение: а) данный
интеграл является интегралом от неограниченной функции (подынтегральная функция
 не определена в точке
не определена в точке ![]() , при
, при ![]() эта функция неограниченно
возрастает).
эта функция неограниченно
возрастает).
По определению имеем
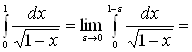 [замена:
[замена: ![]()
![]() ] =
] = 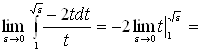
![]() , следовательно, данный
интеграл сходится.
, следовательно, данный
интеграл сходится.
б) по определению
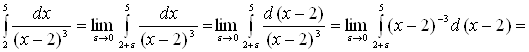
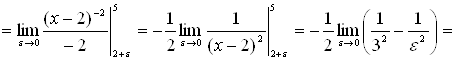
![]() .
.
Значит, данный интеграл является расходящимся.
Литература
1. Ильин В.А., Позняк Э.Г. Основы математического анализа. Ч. I. – М.: Наука, 1982. – 616 с.
2. Гусак А.А. Математический анализ и дифференциальные уравнения. – Мн.: ТетраСистемс, 1998. – 416 с.
3. Гусак А.А. Высшая математика: Учеб. пособие для студентов вузов: В 2 т. – Мн., 1998. – 544 с. (1 т.), 448 с. (2 т.).
4. Кремер Н.Ш., Путко Б.А., Тришин И.М., Фридман М.Н. Высшая математика для экономистов: Учебник для вузов / Под ред. проф. Н.Ш. Кремера. – М.: ЮНИТИ, 2002. – 471 с.
5. Яблонский А.И., Кузнецов А.В., Шилкина Е.И. и др. Высшая математика. Общий курс: Учебник / Под общ. ред. С.А. Самаля. – Мн.: Выш. шк., 2000. – 351 с.