Учебное пособие: Приложения определенного интеграла к решению некоторых задач механики и физики

Учебное пособие: Приложения определенного интеграла к решению некоторых задач механики и физики

Приложения определенного интеграла к решению некоторых задач механики и физики

1. Моменты и центры масс плоских кривых. Если дуга кривой задана уравнением y=f(x), a≤x≤b, и имеет плотность 1) =(x), то статические моменты этой дуги Mx и My относительно коорди­натных осей Ox и Oy равны

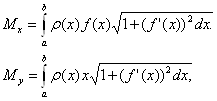
моменты инерции IХ и Iу относительно тех же осей Ох и Оу вычис­ляются по формулам

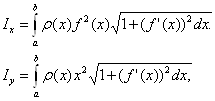
а координаты центра масс  и  — по формулам

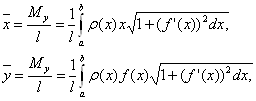
где l— масса дуги, т. е.

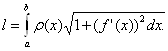
Пример 1. Найти статические моменты и моменты инерции относительно осей Ох

и Оу дуги цепной линии y=chx при 0≤x≤1.

1) Всюду в задачах, где плотность не указана, предполагается, что кривая однородна и =1.

◄ Имеем: Следовательно,

 ►

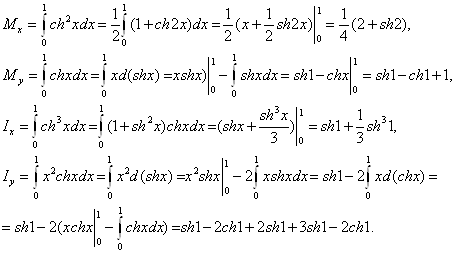Пример 2. Найти координаты центра масс дуги окружности x=acost, y=asint, расположенной в первой четверти.

◄ Имеем:

Отсюда получаем:

►

В приложениях часто оказывается полезной следующая

Теорема Гульдена. Площадь поверхности, образованной вращением дуги плоской кривой вокруг оси, лежащей в плоскости ду­ги и ее не пересекающей, равна произведению длины дуги на длину окружности, описываемой ее центром масс.

 Пример 3. Найти координаты центра масс полуокружности

◄Вследствие симметрии . При вращении полуокружности вок­руг оси Ох получается сфера, площадь поверхности которой равна , а длина полуокружности равна па. По теореме Гульдена имеем

Отсюда , т.е. центр масс C имеет координаты C.

2. Физические задачи. Некоторые применения определенного интеграла при решении физических задач иллюстрируются ниже в примерах 4—7.

Пример 4. Скорость прямолинейного движения тела выражает­ся формулой  (м/с). Найти путь, пройденный телом за 5 секунд от начала движения.

◄ Так как путь, пройденный телом со скоростью (t) за отрезок времени [t1,t2], выражается интегралом

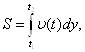
то имеем:

 ►

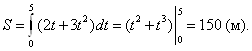Пример 5. Какую работу необходимо затратить для того, чтобы тело массы m поднять с поверхности Земли, радиус которой R, на высоту /i? Чему равна работа, если тело удаляется в беско­нечность?

<4| Работа переменной силы / (#), действующей вдоль оси Ох на от­резке [а, Ь], выражается интегралом